为了更好地理解本篇文章的知识内容,读者可以将以下文章作为补充知识进行阅读 :
(强烈建议阅读,杨辉三角与斐波那契相关性强)
C语言————原码 补码 反码 (超绝详细解释)-优快云博客
在了解杨辉三角前,我们先了解一下二项式系数的基础知识(以下为百度百科中的内容):
什么是杨辉三角?
杨辉三角最早由北宋数学家贾宪提出,南宋数学家杨辉在《详解九章算法》中对其进行了详细记载,因此得名(在国外也被称为 “帕斯卡三角”,因法国数学家帕斯卡后来也独立发现了它)。
他的每一行都是对应次幂二项式展开式每一项的系数,涉及到相关阶乘数据的计算。
每一行中间的数字等于他上方两个数字之和,即:C(n,k)=C(n−1,k−1)+C(n−1,k)
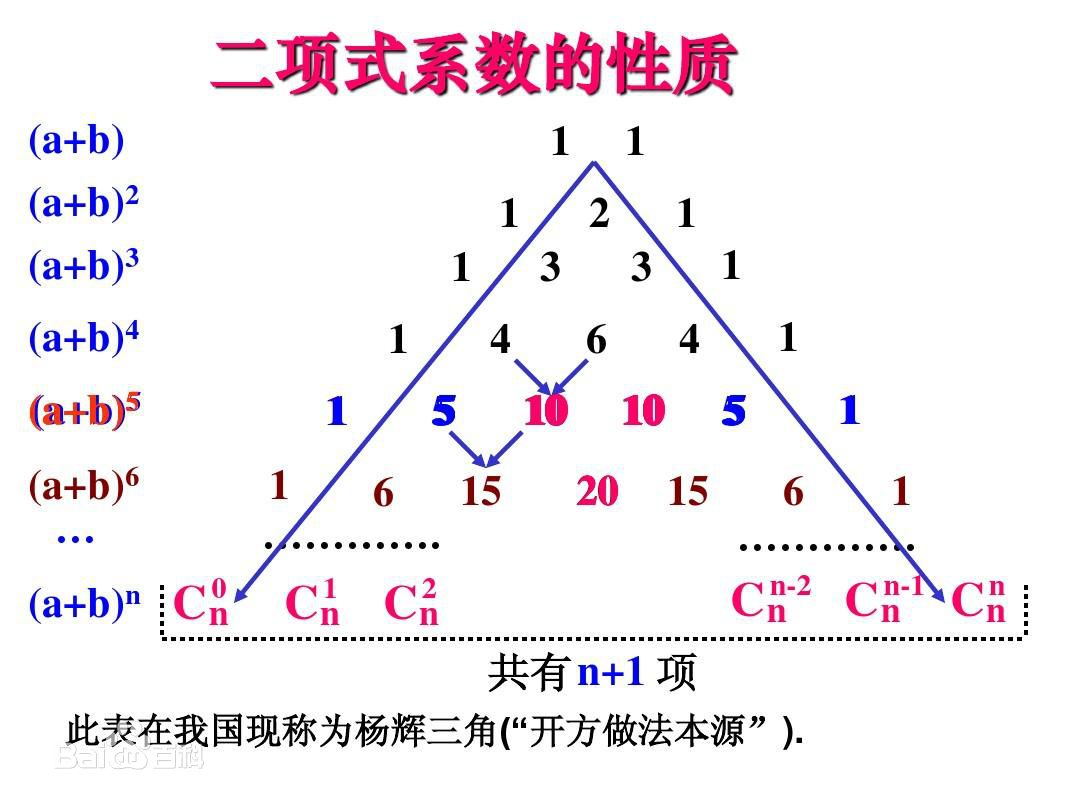
那么我们怎么在C语言中将其打印出来呢?
我们常见的两个方法有:暴力拆解法、递归法。
暴力拆解法
对于每一行的数字,他们值的计算有如下的规律,n代表所在行数,k代表列数,n和k同时可以确认杨辉三角中一个具体位置的数值大小。
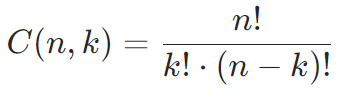
因此我们可以先分解这个计算式,创建如下两个函数;
阶乘函数:
每一个非负整数的阶乘都等于前一个数字的阶乘乘以他自身
int multiply(int x)//求一个数的阶乘
{
if (x == 0)
return 1;
else
return (x * multiply(x - 1));//递归思想
}组合数函数:
int result_1(int x, int y)
{
int a = multiply(y) / multiply(y - x);//两个函数的嵌套使用
return a / multiply(x);
}需注意这两个代码的先后顺序,避免出现报错情况 。
有了这两个函数作为工具,我们可以试着对杨辉三角进行拆解,他的几个重要特性:
1. 行数编号由n = 0起始,每一行的元素个数为n + 1个;
2. 行数为n列数为k的数值可以用result_1(k,n)来求解;
3. 通过输入的行数来限制杨辉三角行数的打印。
具体的实现方式如下:
//主运行程序块
int main()
{
int n = 0;//确认行数
int k;//限制打印的行数
scanf("%d", &k);
while (n <= k)
{
int count = 0;//计算每行的元素个数
for (int i = 0; i <= n; i++)
{
printf("%d ",result_1(i, n));
count++;
if (count >= n + 1)
break;
}
printf("\n");
n++;
}
return 0;
}
递归法
杨辉三角使用递归的方法其实也能在上述代码中看到影子(如阶乘函数),我们知道杨辉三角中每一行中间的数字等于他上方两个数字之和,根据这个特性,我们得到了新的函数:
int result_2(int x, int y)//递归的方法
{
if (x == 0 | x == y)//在两边的值为0
return 1;
else
return result_2(x,y - 1) + result_2(x - 1, y - 1);
}我们将暴力拆解程序块中的 result_1 替换成 result_2 函数,即可完成杨辉三角的打印,具体程序如下:
int main()
{
int n = 0;//确认行数
int k;//限制打印的行数
scanf("%d", &k);
while (n < k)
{
int count = 0;//计算每行的元素个数
int j = 0;//判断打印的第几行
//for(int z = 1;z <= (k - n - 1) ;z ++)//为了打印空格
//{
// printf(" ");
//}
for (int i = 0; i <= n; i++)
{
printf("%d ", result_2(i, n));
count++;
if (count >= n + 1)
break;
}
printf("\n");
n++;
}
return 0;
}不管是暴力拆解法还是递归法,他们的运行结果都是一致的,但递归法会一次次调用函数,这给内存施加压力,因此在打印行数偏大时,优选暴力拆解法,他们运行的结果如下图(以行数5为例子):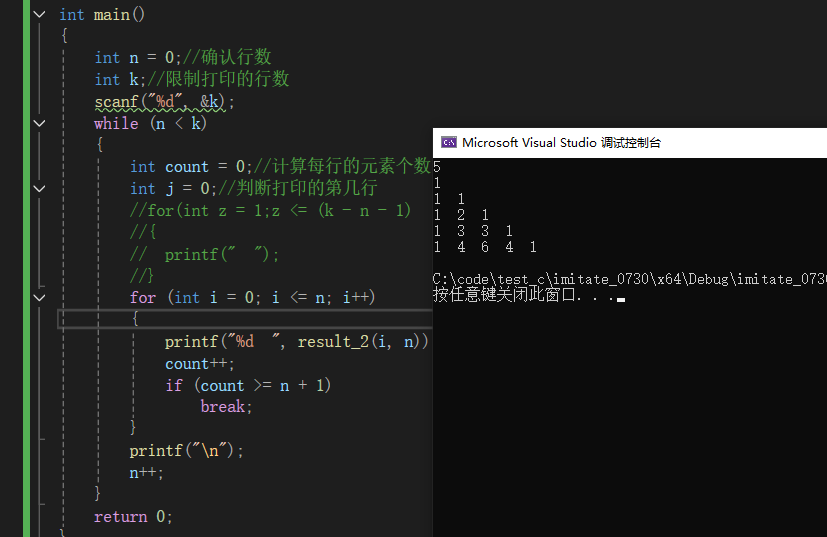
我们可以思考一下 ,那应该如何给他打印成三角形的分布形状呢?
每一行最右边一侧的数字前留的空间会随着行数的上升逐步减少,根据这个特性,我们给他加入了随行数减少的空格打印,具体结果如下: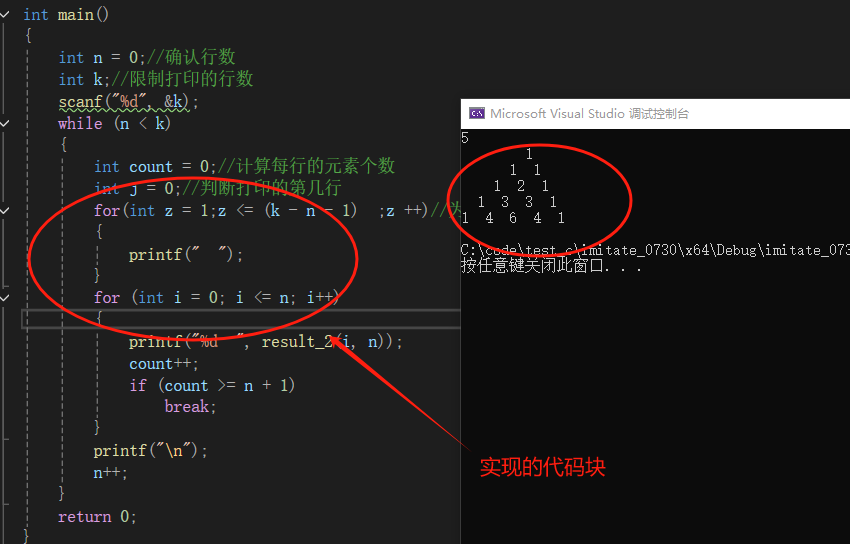
仅供参考,也希望大佬们能够不吝赐教,加深我对杨辉三角的理解。
打怪升级中.........................................................................................................................................






















 11万+
11万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










