rsa4k 需要填充么？填充到多少合适？

是的，RSA在实际应用中必须使用填充方案，直接加密原始数据（无填充）会导致严重的安全问题。具体如下：

为什么RSA需要填充？

1. 防止确定性加密

• 纯RSA（无填充）是确定性的：相同的明文每次加密得到相同的密文，容易被攻击者通过穷举或模式分析破解。
• 填充（如OAEP）会引入随机性，确保相同明文加密后生成不同的密文。

1. 抵抗攻击

• 语义安全：无填充的RSA无法抵抗选择明文攻击（CPA）。例如，攻击者可以通过观察密文推测明文。
• 数学攻击：无填充时，若明文过短（如仅几个字节），可能被小明文攻击或通过数学方法（如Coppersmith算法）恢复明文。

1. 兼容性限制

• RSA算法要求输入数据的长度必须小于或等于模数（密钥长度）的字节数，填充会将较短明文扩展至匹配长度。例如，2048-bit RSA的输入必须是256字节。

示例：OAEP填充的作用：

假设用2048-bit RSA加密明文 "Hello"：

1. 无填充：直接加密 "Hello"（仅5字节），不符合RSA输入长度要求，且易被破解。
2. OAEP填充：

• 添加随机盐值（如 "s8df3k"）和哈希处理。
• 扩展为256字节的密文，每次加密结果不同，即使明文相同。

填充到多少合适？

1，填充后的总长度要求

• 目标：填充后的明文必须等于RSA密钥的模数长度（单位：字节）。

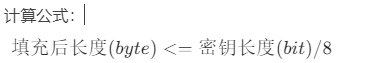
例如：

• 2048-bit RSA → 填充到 256字节（2048 ÷ 8）。
• 3072-bit RSA → 填充到 384字节

2. 不同密钥长度的填充容量

不同填充方案对明文的长度限制不同（需预留空间给填充结构）：

填充方案	最大明文长度（公式）	示例（2048-bit密钥）
PKCS#1 v1.5	密钥长度/8 - 11字节	256 - 11 = 245字节
OAEP	密钥长度/8 - 2*哈希输出长度 - 2字节	256 - 2*32 - 2 = 190字节（SHA-256）

注：OAEP的明文空间更小，因为其填充结构更复杂（包含哈希和随机盐值）

2048位RSA密钥（最常见）

填充方案	填充后最大长度	最大明文长度（字节）	计算逻辑
PKCS#1 v1.5	256 bytes(2048 位)	245字节 (1960位)	2048/8−11=256−11=245
OAEP (SHA-256)	256 bytes(2048 位)	190字节 (1520位)	256−42≈214（实际更少）

4096位RSA密钥

填充方案	填充后最大长度	最大明文长度（字节）	计算逻辑
PKCS#1 v1.5	512 bytes(4096 位)	501字节 (4008位)	4096/8−11=512−11=501
OAEP (SHA-512)	512 bytes(4096 位)	446字节 (3568位)	512−66≈446

3，为什么不能填满所有位？

• 随机性要求：填充必须包含随机数（如PKCS#1 v1.5的8字节随机数），否则可能遭受攻击。
• 格式标记：填充方案需要保留部分字节标识结构（如OAEP的哈希和分隔符）。

超长明文如何处理？

若明文超过填充后的可用空间：

1, 分段加密：将明文分成多个块，每块单独填充加密（效率低，不推荐）。

2, 改用混合加密：

（1）用对称密钥加密实际明文如AES-256（更高效且无长度限制）。

（2）然后使用RSA加密一个 ,对称密钥生成的密文。

3，结合 hash：

（1）使用 SHA-512，将铭文进行 hash，生成 message digest。

（2）然后使用RSA加密 message digest

总结

• 必须填充：避免安全漏洞，确保语义安全（Semantic Security）。
• 推荐方案：优先使用OAEP（如RSAES-OAEP-SHA-256），填充后占满密钥长度（如512字节）。
• 旧系统妥协：若必须用PKCS#1 v1.5，确保明文不超过 密钥长度 - 11字节。

通过正确填充，RSA-4096可安全用于加密敏感数据（如会话密钥、身份令牌等）。