这玩意就像有人问:人耳难道是每时每刻在做傳立叶变换吗?
答案:是的,但人耳是用空间换时间,不用迭代方程

我们现在使用的电脑和GPU都采用数字计算方式,通过0和1的二进制系统进行运算,虽然计算精度很高,但在处理某些复杂的数学问题时,不仅速度慢,还特别耗电。
还存在另一种被称为模拟计算的方法,它直接借助电路的物理特性来获得计算结果,运行速度极快,能耗也很低,但长期以来的一个致命缺陷就是计算精度不够准确。
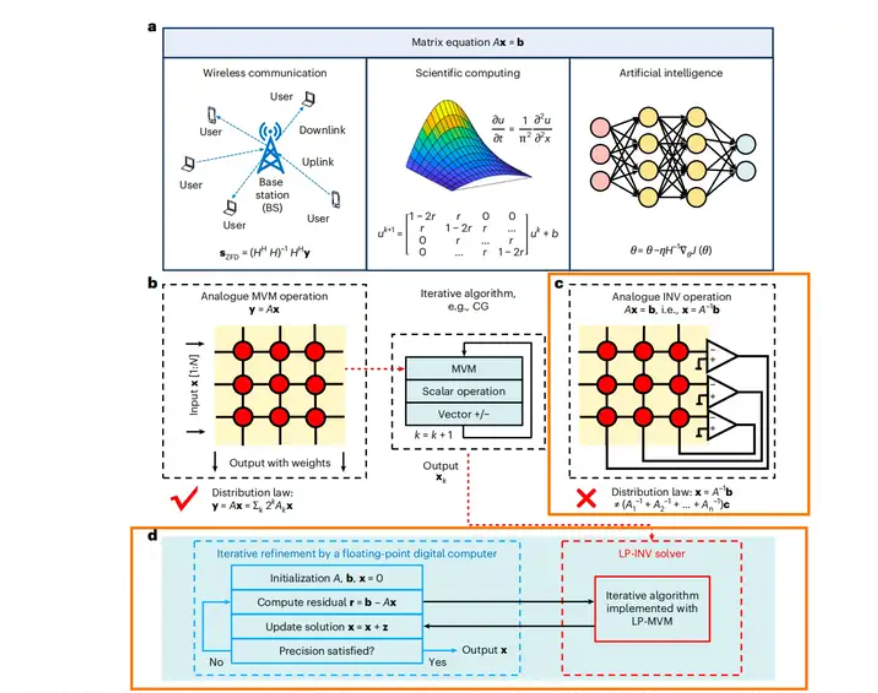
这个本质上不是概率的问题,这是模糊计算的问题。我们期盼这种特性很久了,大部分的机器学习计算都是过度精确的——我只是要一个权重加成,接近就行,但现在的计算基本上都是每步都是精确的,非常浪费。如果这个技术真的实用,机器学习会发生翻天覆地的进步。
论文自己说的:预期应用场景涵盖无线通信中的信号处理、科学计算中的微分方程求解以及人工智能领域的神经网络训练。无线通信不懂,可能契合,比如6G。微分方程求解与神经网络训练,暂时没人会用这个技术。专用性强,通用性还不足。
来还想这不要是把量子实验说成量子计算的糊弄玩意儿。看了一下感觉这个其实还挺有用的。

我仔细看了下论文的补充材料,里面(Supplementary Note 2)证明了算法的收敛条件:spectral radius of (I - A*A0⁻¹) < 1。只要满足这个条件,迭代就一定会收敛到精确解(当然得在模拟电路误差合理范围内)。
关于实质证据,我看性能对比(图5c/d)确实是推算,不过它是基于实验数据。论文在图5a 和 5b 中用示波器实测了核心模拟运算的瞬态响应时间(求逆约120ns,乘法约60ns)。
当然,还得等复现了。我感觉可信度挺高的。
举个例子,比如有两个结果值,它们的计算过程开销都比较大。而我要比较两个结果值的大小,实际上大部分情况我不需要求出两个数的精确值,只要两个数的估算值不是很接近,那么直接比较估算值就可以。其实这种场景非常常见,以至于一些调用频繁的地方值得单独写个估算方法。

而如果在硬件层面上就支持这么做就有可能得到很大的提升。
以当下国内在通信技术领域的活跃程度来说,这种技术但凡有效,就会很快在产业界得到发展,甚至应用的。
08年刚刚出现的polar编码技术,在产业界的积极推动下,16年都成了行业标准技术了。
这个芯片解决什么问题?
该芯片直击大模型算力瓶颈的根源:矩阵乘加运算。
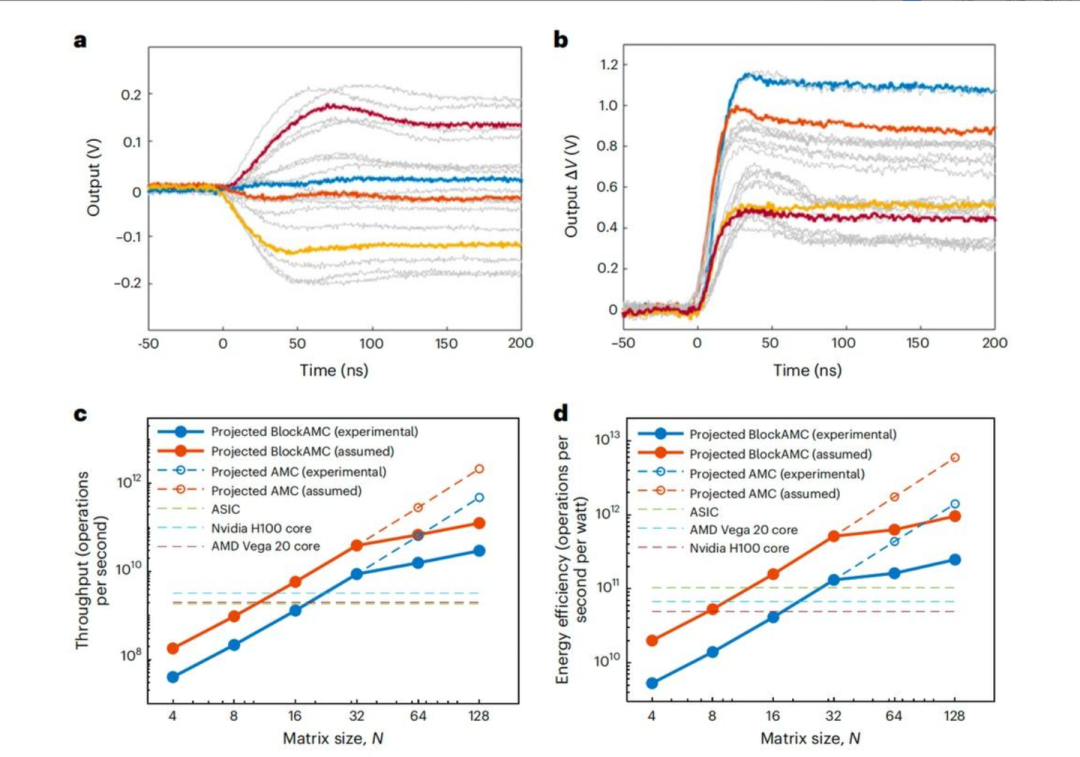
传统数字计算在处理这一核心任务时能耗效率低下。此项研究转向模拟计算,通过物理定律直接实现矩阵运算,在理论上实现了速度和能效的飞跃。
该路径因精度缺陷及误差累积问题,难以应用于大模型。北大团队的核心突破在于提出了全模拟迭代精炼框架,从而有效解决了精度难题。
有大疑问,一堆adc dac 串联, 测量误差先不说, 首先他要迭代几次, 这个频率能用在6g上吗?我猜测让人隐藏的事实是这个电路只是并行计算,并不能高频操作。
但是模拟算不了浮点数,看问题详情写的也是24bit定点,对ai的训练作用十分有限,倒是可以尝试用于推理芯片
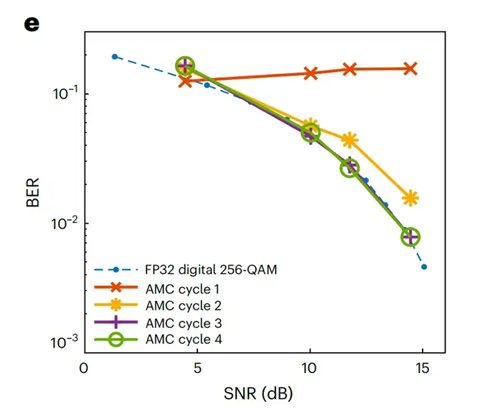
SNN我觉得理论上还是有潜力的。就是训练,推理,框架算法没有突破,而没有突破性算法和应用成果前,更加没人力物力愿意投入。CNN也是很早就有,但是真正吸引人力物力资源,也是alexnet的突破性进展让人见识到它的厉害以后,短短十几年,发展成这样的规模。更早的BP网络发展规律也是。SNN也需要这样一次算法与硬件联合的突破性成果来吸引目光。
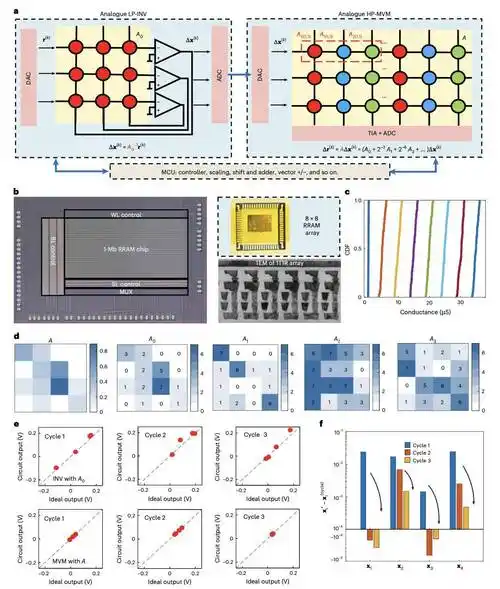
模拟计算最大的大坑是温漂问题,实验室跑的好好的扔机柜里80度试试?早就被淘汰的老黄历了,谁不知道数字电路效率没模拟电路高,本质上就是为了稳定性牺牲效率。
当然,也可以尝试通过组合多个定点单元实现浮点计算,但是这样优越性可能就不明显了
拿来AI炼丹岂不是很好用?反正都是矩阵运算,跟DeepSeek合作一下推出一个DeepSeek-MIMO,由于自带一些随机性没准能整出来什么新花样也说不定。。。。





















 1665
1665

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










