LeetCode131.分割回文串:
题目描述:
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是
回文串
。返回 s 所有可能的分割方案。
示例 1:
输入:s = “aab”
输出:[[“a”,“a”,“b”],[“aa”,“b”]]
示例 2:
输入:s = “a”
输出:[[“a”]]
提示:
1 <= s.length <= 16
s 仅由小写英文字母组成
思路:
一看这种数据很短,但是看起来比较复杂的问题,就揪一下它的最大可能次数: 比如字符串长度为n,且全是相同字母,那么方案数是需要在n-1个空中任意组合,每个空可以分割或者不分割,总的方案数最坏情况是2^(n-1),是指数级别的,那么就可以断定是爆搜问题。
对于这题来说,我们可以先扫描一遍,判断哪些段[i ~ j]是回文段是可以的,但更好的做法是用一个数组来存储原字符串中i~j是否为回文串f[i][j]: 递归来做,f[i][j]为回文串,前提是s[i] == s[j] 并且 f[i + 1][j - 1]已经是回文串了,以此递推下去,将整个原字符串中所有回文段全部存储下来,但是这里有个需要注意的就是f[i][j]是由f[i + 1][j - 1]推出来的,所以我们需要先求出f[i + 1][j - 1],同时j是在i的后面的, 所以我们先枚举j!!!(细节很重要)
dfs:爆搜:由于已经记录了原字符串中i ~j 是否为回文串,所以我们从第0个字符开始搜索所有方案,从前往后枚举每一个字符,只要枚举到的位置跟开始位置之间的字符段是回文串,那么就将它截取出来放到当前搜索路径中,同时进入下一层搜索(从当前枚举的位置的下一个位置开始),将当前搜索完之后一定要记得将当前路径加入的当前字符段清掉,恢复现场, 保证下一段回文段的搜索不被打乱
当搜到s的最后一个字符就是结束,将整条搜索路径加入答案集合中
时间复杂度:
首先考虑最多有多少个合法方案,我们可以考虑在相邻字符之间放板子,每种放板子的方法都对应一种划分方案,而每个字符间隔有放和不放两种选择,所以总共有 2^n−1
个方案。另外对于每个方案,需要 O(n)的时间记录方案。所以总时间复杂度是 O(2^n)*n
注释代码:
class Solution {
public:
vector<vector<bool>> f;
vector<vector<string>> res;
vector<string> path;
vector<vector<string>> partition(string s) {
int n = s.size();
//f[i][j]表示原字符串的i~j这段是否为回文串
f = vector<vector<bool>> (n, vector<bool>(n));
for(int j = 0; j < n; j++) //要先求出f[i + 1][j - 1]所以先枚举j
{
for(int i = 0; i <= j; i++)
{
if(i == j) f[i][j] = true; //只有一个单词肯定是回文串
else if(s[i] == s[j])
{
//只有两个字符(还相同),或者是原字符串中i+ 1 ~ j - 1是回文串,那么f[i][j]肯定也是回文串
if(i + 1 > j - 1 || f[i + 1][j - 1]) f[i][j] = true;
}
}
}
dfs(s, 0); //找出所有方案,从第0个字符开始搜
return res;
}
void dfs(string&s, int u)
{
if(u == s.size()) res.push_back(path);
else{
for(int i = u; i < s.size(); i++)
{
if(f[u][i])
{
path.push_back(s.substr(u, i - u + 1));
dfs(s, i + 1);
path.pop_back();
}
}
}
}
};
纯享版:
class Solution {
public:
vector<vector<bool>> f;
vector<string> path;
vector<vector<string>> res;
vector<vector<string>> partition(string s) {
int n = s.size();
f = vector<vector<bool>> (n, vector<bool> (n));
for(int j = 0; j < n; j++)
{
for(int i = 0; i <= j; i++)
{
if(i == j) f[i][j] = true;
else if(s[i] == s[j])
{
if(i + 1 > j - 1 || f[i + 1][j - 1]) f[i][j] = true;
}
}
}
dfs(s, 0);
return res;
}
void dfs(string& s, int u )
{
if(u == s.size()) res.push_back(path);
else{
for(int i = u; i < s.size(); i++)
{
if(f[u][i])
{
path.push_back(s.substr(u, i - u + 1));
dfs(s, i + 1);
path.pop_back();
}
}
}
}
};
LeetCode132.分割回文串Ⅱ:
题目描述:
###一开始直接考虑使用上题的path.size()进行判断,但是上一题的时间复杂度是O(2^n * n),会超时,所以爆搜方案肯定是不能用的,需要使用DP优化:用一个状态来表示一种方案
class Solution {
public:
vector<vector<bool>> f;
int res = INT_MAX;
vector<string> path;
int minCut(string s) {
int n = s.size();
//f[i][j]表示原字符串的i~j这段是否为回文串
f = vector<vector<bool>> (n, vector<bool>(n));
for(int j = 0; j < n; j++) //要先求出f[i + 1][j - 1]所以先枚举j
{
for(int i = 0; i <= j; i++)
{
if(i == j) f[i][j] = true; //只有一个单词肯定是回文串
else if(s[i] == s[j])
{
//只有两个字符(还相同),或者是原字符串中i+ 1 ~ j - 1是回文串,那么f[i][j]肯定也是回文串
if(i + 1 > j - 1 || f[i + 1][j - 1]) f[i][j] = true;
}
}
}
dfs(s, 0); //找出所有方案,从第0个字符开始搜
return res;
}
void dfs(string&s, int u)
{
if(u == s.size()){
int t = path.size();
if(t > 0) res = min(res, t - 1);
}else{
for(int i = u; i < s.size(); i++)
{
if(f[u][i])
{
path.push_back(s.substr(u, i - u + 1));
dfs(s, i + 1);
path.pop_back();
}
}
}
}
};
思路:
使用DP优化:用一个状态来表示一种方案=>设定集合f[i]: s[1~i]的所有分割方案,属性是最小值: 利用上一题的确定回文段的维护数组,在s[1 ~i]中的所有分割方案就是根据回文段数组来分割的,那么1 ~ i的分割方案求最小值的状态划分以最后一段回文段来划分,比如k ~i,那么1 ~i的最小分割方案就是1 ~ k -1的最小方案数加当前最后一段: f[i] = f[k -1] + 1
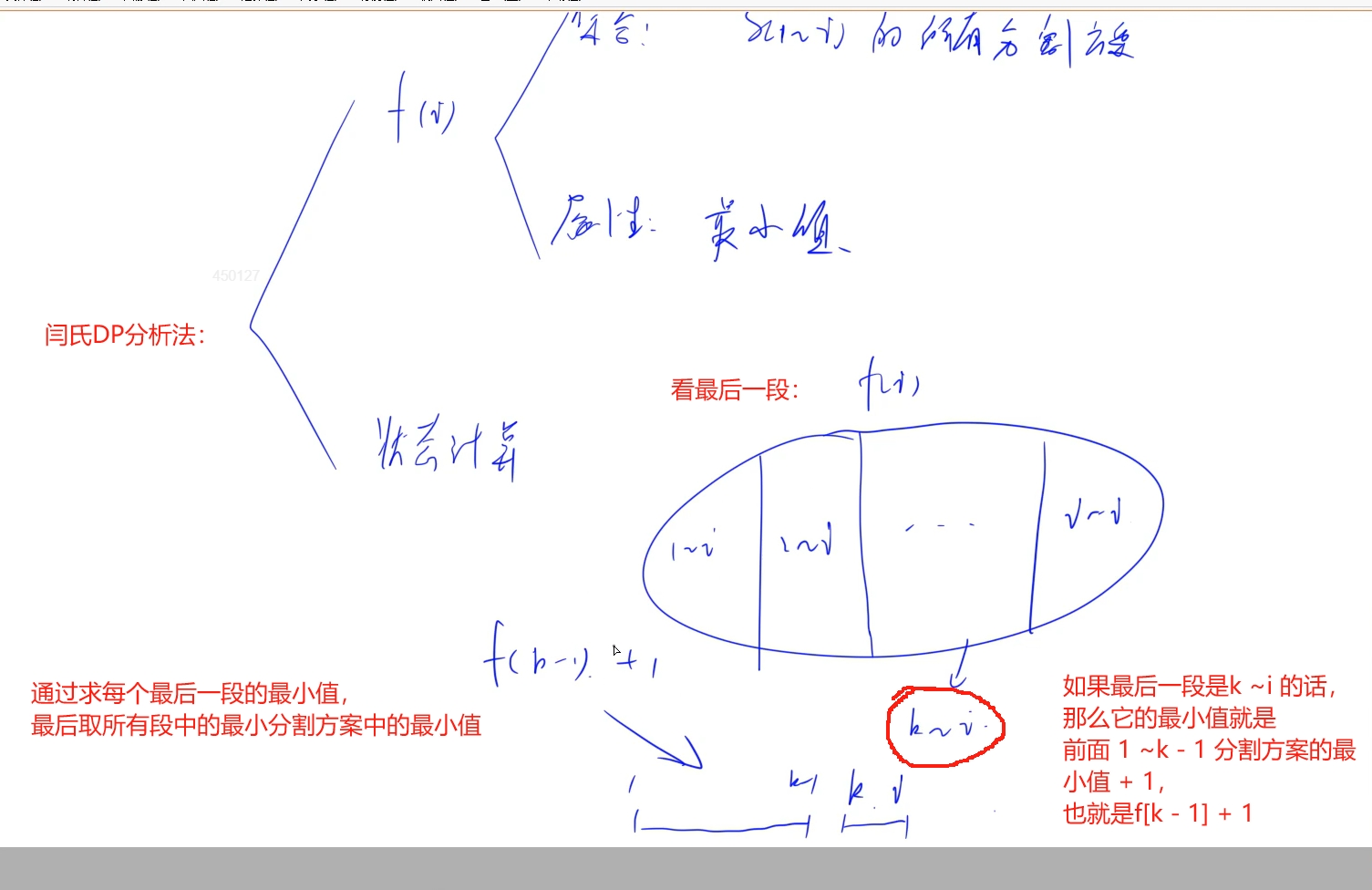
时间复杂度:
求回文段数组O(nn), DP状态也是O(nn)的,所以总的时间复杂度是O(n*n)的

注释代码:
class Solution {
public:
int minCut(string s) {
int n = s.size();
s = ' ' + s;
vector<vector<bool>> g(n + 1, vector<bool>(n + 1));
vector<int> f(n + 1, 1e8);
for(int j = 1; j <= n; j++)
{
for(int i = 1; i <= n; i++)
{
if(i == j) g[i][j] = true;
else if(s[i] == s[j])
{
if(i + 1 > j - 1 || g[i + 1][j - 1]) g[i][j] = true;
}
}
}
f[0] = 0;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= i; j++)
{
if(g[j][i]) //j在前i在后
{
//如果j ~ i 这段是回文段的话,将它作为最后一段,那么f[i] = f[j - 1] + 1
f[i] = min(f[i], f[j - 1] + 1);
}
}
}
return f[n] - 1;
}
};
纯享版:
class Solution {
public:
int minCut(string s) {
int n = s.size();
s = ' ' + s;
vector<vector<bool>> g(n + 1, vector<bool> (n + 1));
vector<int> f(n + 1, 1e8);
for(int j = 1; j <= n; j++)
{
for(int i = 1; i <= j; i++)
{
if(i == j) g[i][j] = true;
else if(s[i] == s[j])
{
if(i + 1 > j - 1 || g[i + 1][j - 1]) g[i][j] = true;
}
}
}
f[0] = 0;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= i; j++)
{
if(g[j][i])
{
f[i] = min(f[i], f[j - 1] + 1);
}
}
}
return f[n] - 1;
}
};
LeetCode133.克隆图:
题目描述:
给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。
图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
class Node {
public int val;
public List neighbors;
}
测试用例格式:
简单起见,每个节点的值都和它的索引相同。例如,第一个节点值为 1(val = 1),第二个节点值为 2(val = 2),以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点(值为 1)。你必须将 给定节点的拷贝 作为对克隆图的引用返回。
示例 1:
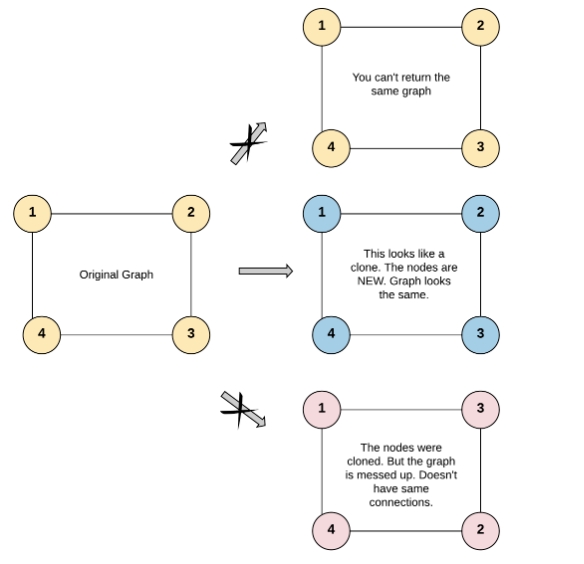
输入:adjList = [[2,4],[1,3],[2,4],[1,3]]
输出:[[2,4],[1,3],[2,4],[1,3]]
解释:
图中有 4 个节点。
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
节点 3 的值是 3,它有两个邻居:节点 2 和 4 。
节点 4 的值是 4,它有两个邻居:节点 1 和 3 。
示例 2:

输入:adjList = [[]]
输出:[[]]
解释:输入包含一个空列表。该图仅仅只有一个值为 1 的节点,它没有任何邻居。
示例 3:
输入:adjList = []
输出:[]
解释:这个图是空的,它不含任何节点。
提示:
这张图中的节点数在 [0, 100] 之间。
1 <= Node.val <= 100
每个节点值 Node.val 都是唯一的,
图中没有重复的边,也没有自环。
图是连通图,你可以从给定节点访问到所有节点。
思路:
先复制所有点,在将每个点之间的边复制下来
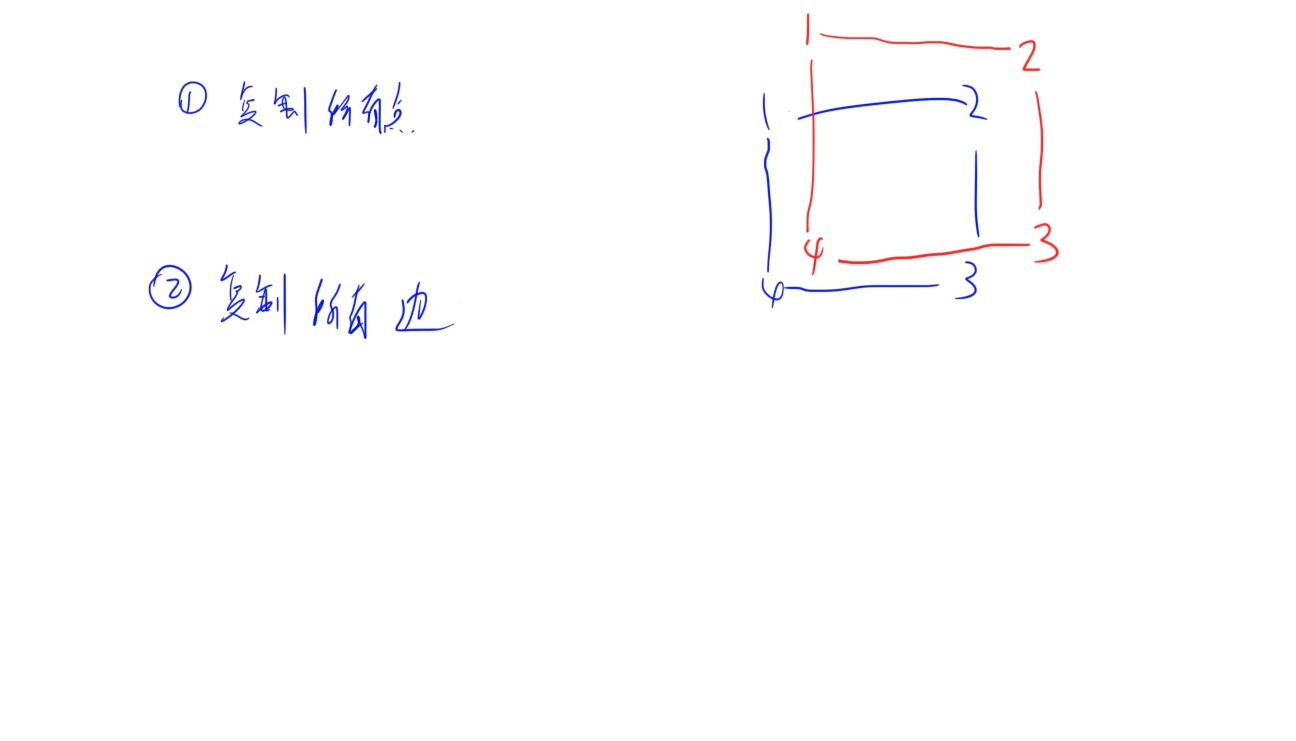
时间复杂度:每个点每条边遍历一次,时间复杂度是O(m)的,m为边数
注释代码:
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> neighbors;
Node() {
val = 0;
neighbors = vector<Node*>();
}
Node(int _val) {
val = _val;
neighbors = vector<Node*>();
}
Node(int _val, vector<Node*> _neighbors) {
val = _val;
neighbors = _neighbors;
}
};
*/
class Solution {
public:
unordered_map<Node*, Node*> hash; //存点的映射
Node* cloneGraph(Node* node) {
if(!node) return NULL;
dfs(node); //复制所有点
for(auto [s, d] : hash) //取出每个点及其映射
{
for(auto ver : s -> neighbors) //找出遍历到的点的所有邻点 ,(存在的边)
{
d -> neighbors.push_back(hash[ver]); //将所有邻点同样添加为映射的邻点,相当于建边
}
}
return hash[node];
}
void dfs(Node* node)
{
hash[node] = new Node(node -> val); //复制当前点到hash中并一起存储下来
for(auto ver : node -> neighbors) //遍历当前点的所有邻点
{
if(hash.count(ver) == 0) //如果当前的邻点没有复制过
{
dfs(ver); //递归下去
}
}
}
};
纯享版:
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> neighbors;
Node() {
val = 0;
neighbors = vector<Node*>();
}
Node(int _val) {
val = _val;
neighbors = vector<Node*>();
}
Node(int _val, vector<Node*> _neighbors) {
val = _val;
neighbors = _neighbors;
}
};
*/
class Solution {
public:
unordered_map<Node*, Node*> hash;
Node* cloneGraph(Node* node) {
if(!node) return NULL;
dfs(node);
for(auto [s, d] : hash)
{
for(auto ver : s -> neighbors)
{
d -> neighbors.push_back(hash[ver]);
}
}
return hash[node];
}
void dfs(Node* node)
{
hash[node] = new Node(node -> val);
for(auto ver : node -> neighbors)
{
if(hash.count(ver) == 0)
{
dfs(ver);
}
}
}
};
2024/12/13二刷:
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> neighbors;
Node() {
val = 0;
neighbors = vector<Node*>();
}
Node(int _val) {
val = _val;
neighbors = vector<Node*>();
}
Node(int _val, vector<Node*> _neighbors) {
val = _val;
neighbors = _neighbors;
}
};
*/
class Solution {
public:
unordered_map<Node*, Node*> hash;
Node* cloneGraph(Node* node) {
if(!node) return NULL;
dfs(node);
for(auto [s, t] : hash)
{
for(auto ver : s -> neighbors)
{
t -> neighbors.push_back(hash[ver]);
}
}
return hash[node];
}
void dfs(Node* node)
{
hash[node] = new Node(node -> val);
for(auto s : node -> neighbors)
{
if(hash.count(s) == 0) dfs(s);
}
}
};
LeetCode134.加油站:
题目描述:
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1304
1304

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








