如图,设点$M(x_0,y_0)$是椭圆$C:\dfrac{x^2}{2}+y^2=1$上一点,从原点$O$向圆$M:(x-x_0)^2+(y-y_0)^2=\dfrac{2}{3}$作两条切线分别与椭圆$C$交于$P,Q$,直线$OP,OQ$的斜率分别为$k_1,k_2$
(1)求证:$k_1k_2$为定值
(2)求四边形$OPQM$面积的最大值.



分析:涉及到面积最大容易想到仿射变换:
(1)
$$\begin{cases}
x^{'}&=x\\
y^{'}&=\sqrt{2}y
\end{cases}$$
则$k^{'}=\sqrt{2}k$,由蒙日圆性质得$k_1^{'}k_2^{'}=-1$故$k_1k_2=-\dfrac{1}{2}$
(2)如图$S=\dfrac{1}{\sqrt{2}}(S_1+S_2)=\dfrac{1}{\sqrt{2}}(sin\alpha+cos\alpha)\le1$
第二小问常规方法提示:

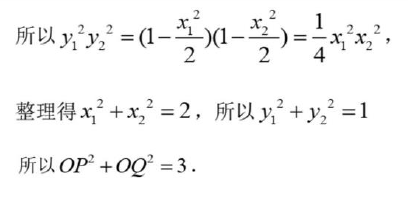




 本文探讨了椭圆上的点与特定圆之间的几何关系,通过仿射变换和蒙日圆性质证明了从原点到该圆的两条切线斜率乘积为定值,并求解了相关四边形面积的最大值。
本文探讨了椭圆上的点与特定圆之间的几何关系,通过仿射变换和蒙日圆性质证明了从原点到该圆的两条切线斜率乘积为定值,并求解了相关四边形面积的最大值。
















 1456
1456

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








