【数据结构】二叉搜索树的认识和基本操作

最新推荐文章于 2025-10-13 14:42:05 发布
原创 最新推荐文章于 2025-10-13 14:42:05 发布 · 357 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文详细介绍了二叉搜索树的基本概念、操作方法及其代码实现。包括查找、插入、删除节点等核心操作，并提供了完整的C语言代码示例。

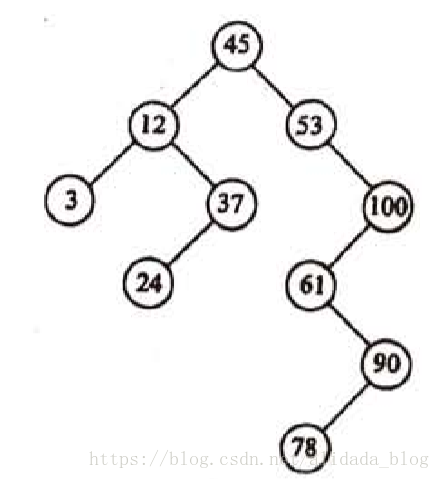
一.二叉搜索树的概念
     二叉搜索树又称二叉排序树，他或者是一颗空树，或者具有以下性质的二叉树：
         1.若他的左子树不为空，则左子树上的值都小于根结点上的值
         2.若他的右子树不为空，则右子树上的值都大于根结点上的值
         3.他的左右子树也分别为二叉搜索树
 



二.二叉搜索树的操作
    1.查找
       （1.）若根结点不为空且要查找的data == pRoot(根节点的值)，则返回ture
         (2.)若要查找的data>pRoot(根结点的值)，则在他的右子树查找
       （3.）若查找的data<pRoot(根结点的值)，则在他的左子树查找

         如果没找打返回false
 

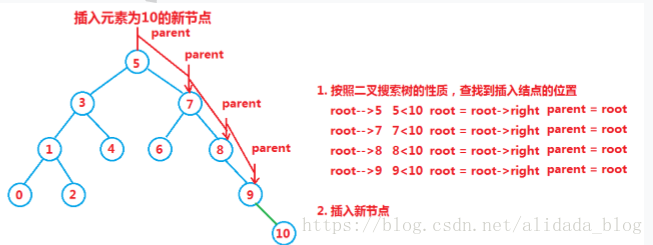
    2.插入
       在二叉树中插入新元素时，必须先检测该元素是否在树中已经存在，如果存在在不进行插入，否则将新元素加入到元素搜索截至的地方。

        （1.）若树为空，则直接插入
        （2.）树不为空时，按二叉搜索树的性质查找插入位置，插入新节点。

            
    3.删除

        （1.）如果没有右孩子或者左右孩子都没有则直接删除
        （2.）删除该节点且将被删除节点的双亲结点指向被删除结点的左孩子结点。

        （3.）删除该节点且使删除节点的双亲结点指向被删除结点的右孩子结点。
        （4.）在他的右子树中寻找中序下的第一个结点（最小结点），用它的值填补到被删除结点中，再来处理该节点的删除问题

                 左子树中找替代结点----->最右边的结点----->最大的结点
                 右子树中找替代结点----->最左边的结点----->最小的结点
   4.遍历
   5.销毁

代码实现
BST.h
#pragma once
#include<stdio.h>
#include<assert.h>
#include<malloc.h>
#include<Windows.h>

typedef int DataType;
typedef struct BSTreeNode
{
	struct BSTreeNode* _pLeft;
	struct BSTreeNode* _pRight;
	DataType _data;
}BSTNode,*PBSTNode;

// 初始化二叉搜索树 
void InitBSTree(BSTNode** pRoot);

// 插入值为data的元素 
void NorInsertBSTree(BSTNode** pRoot, DataType data);

// 删除值为data的结点 
void NorDeleteBSTree(BSTNode** pRoot, DataType data);

// 在二叉搜索树中查找值为data的结点 
BSTNode* NorFindBSTree(BSTNode* pRoot, DataType data);

// 中序遍历二叉搜索树 
void PreOrder(BSTNode* pRoot);

// 销毁二叉搜索树 
void DestroyBSTree(BSTNode** pRoot);




// 递归实现二叉搜索树中查找、插入和删除方法
// 以递归方式实现二叉搜索树 
BSTNode* FindBSTree(BSTNode* pRoot, DataType data);
void InsertBSTree(BSTNode** pRoot, DataType data);
void DeleteBSTree(BSTNode** pRoot, DataType data);

BST.c
#include"bst.h"

// 初始化二叉搜索树 
void InitBSTree(PBSTNode* pRoot)
{
	assert(pRoot);


	*pRoot = NULL;

}

//创建新节点
PBSTNode BuyNewNode(DataType data)
{
	PBSTNode pcur = NULL;
	pcur = (PBSTNode)malloc(sizeof(BSTNode));
	if (NULL == pcur)
	{
		printf("申请失败！！");
		return 0;
	}

	pcur->_data = data;
	pcur->_pLeft = NULL;
	pcur->_pRight = NULL;

	return pcur;

}



// 插入值为data的元素 
void NorInsertBSTree(PBSTNode* pRoot, DataType data)
{
	PBSTNode pcur = *pRoot;
	PBSTNode parent = NULL;

	if (NULL == *pRoot)
	{
		*pRoot = BuyNewNode(data);
		return;
	}

	
	while (pcur)
	{
		//向左插入
		if (pcur->_data > data)
		{
			parent = pcur;
			pcur = pcur->_pLeft;
		}

		//向右插入
		else if (pcur->_data < data)
		{

			parent = pcur;
			pcur = pcur->_pRight;

		}

		//数据相等
		else
			return;
	}

	if (data > parent->_data)
		parent->_pRight = BuyNewNode(data);

	else
		parent->_pLeft = BuyNewNode(data);
}

// 中序遍历二叉搜索树 
void PreOrder(PBSTNode pRoot)
{
	
	if (pRoot)
	{
		PreOrder(pRoot->_pLeft);
		printf("%d-->", pRoot->_data);
		PreOrder(pRoot->_pRight);

	}

}



// 删除值为data的结点 
void NorDeleteBSTree(PBSTNode* pRoot, DataType data)
{

	PBSTNode pcur = *pRoot;
	PBSTNode parent = NULL;


	assert(pRoot);
	if (NULL == *pRoot)
		return;

	//先找到待删除节点
	while (pcur)
	{
		if (data == pcur->_data)
			break;

		else if (data > pcur->_data)
		{
			parent = pcur;
			pcur = pcur->_pRight;
		}

		else
		{
			parent = pcur;
			pcur = pcur->_pLeft;

		}
	}

	//如果循环出来pcur为空则没有data值直接返回
	if (NULL == pcur)
		return;

	else
	{
		//如果待删除节点没有右子树或者左右子树都没有则直接删除
		if (!(pcur->_pRight))
		{
			if (pcur->_data > parent->_data)
				parent->_pRight = pcur->_pRight;

			else
				parent->_pLeft = pcur->_pLeft;
		}

		//如果没有左子树直接删除
		else if (!(pcur->_pLeft))
		{
			if (pcur->_data > parent->_data)
				parent->_pRight = pcur->_pRight;

			else
				parent->_pLeft = pcur->_pLeft;


		}

		//如果左右子树都在
		else 
		{
			//那就需要找一个替代节点
			//1.右子树中-->找最小的节点--->即右子树中最左的节点
			//2.左子树中-->找最大的节点--->即左子树中最右的节点
			PBSTNode ptr = pcur;
			parent = pcur;
			pcur = pcur->_pLeft;

			while (pcur->_pRight)
			{
				parent = pcur;
				pcur = pcur->_pRight;

			}
			//用左子树中最大的节点替换带删除节点
			ptr->_data = pcur->_data;
			
			//判断代替节点是其双亲的什么节点

			//如果是其左节点
			if (pcur == parent->_pLeft)
				parent->_pLeft = pcur->_pRight;

			else
				parent->_pRight = pcur->_pRight;
		}
	}

	free(pcur);
}




// 在二叉搜索树中查找值为data的结点 
BSTNode* NorFindBSTree(PBSTNode pRoot, DataType data)
{

	PBSTNode pcur = pRoot;

	assert(pRoot);
	if (NULL == pRoot)
		return 0;

	

	while (pcur)
	{
		if (data > pcur->_data)
		{

			pcur = pcur->_pRight;

		}

		else if (data < pcur->_data)
		{

			pcur = pcur->_pLeft;
		}

		else
			return pcur;
	}
}





// 销毁二叉搜索树 
void DestroyBSTree(PBSTNode* pRoot)
{
	assert(pRoot);
	if (*pRoot)
	{
		DestroyBSTree(&(*pRoot)->_pLeft);
		DestroyBSTree(&(*pRoot)->_pRight);
		free(*pRoot);
		(*pRoot)->_data = NULL;

	}

}




//递归实现在二叉搜索树种查找一个值
BSTNode* FindBSTree(PBSTNode pRoot, DataType data)
{
	PBSTNode pcur = pRoot;

	if (NULL == pRoot)
		return 0;

	if (data == pcur->_data)
		return pcur;

	else if (data > pcur->_data)
		return FindBSTree(pcur->_pRight, data);
	else
		return FindBSTree(pcur->_pLeft, data);

}


//递归方法插入元素
void InsertBSTree(PBSTNode* pRoot, DataType data)
{
	assert(pRoot);

	if (NULL == *pRoot)
		*pRoot = BuyNewNode(data);

	else if (data > (*pRoot)->_data)
		InsertBSTree(&(*pRoot)->_pRight, data);

	else if (data < (*pRoot)->_data)
		InsertBSTree(&(*pRoot)->_pLeft, data);

	else
		return;
}


//递归方法删除元素
void DeleteBSTree(PBSTNode* pRoot, DataType data)
{
	assert(pRoot);

	if (NULL == *pRoot)
		return;

	else
	{

		//如果data大则在右子树中找
		if (data > (*pRoot)->_data)
			DeleteBSTree(&(*pRoot)->_pRight, data);

		//如果data小则在左子树中找
		else if (data < (*pRoot)->_data)
			DeleteBSTree(&(*pRoot)->_pLeft, data);

		else
		{
			//如果没有右子树或者左右子树都没有
			//直接删
			BSTNode* pDel = *pRoot;
			if (!(*pRoot)->_pRight)
			{
				*pRoot = pDel->_pLeft;
				free(pDel);
			}

			//如果没有左子树，也直接删
			else if (!(*pRoot)->_pLeft)
			{
				*pRoot = pDel->_pRight;
				free(pDel);
			}

			//如果左右子树都存在
			else
			{
				//到*pRoot右子树找最小节点--最左边
				pDel = (*pRoot)->_pRight;

				while (pDel->_pLeft)
					pDel = pDel->_pLeft;

				//将代替节点的值交给*pRoot
				(*pRoot)->_data = pDel->_data;

				//在*pRoot的右子树删除值为pDel->data的节点
				DeleteBSTree(&(*pRoot)->_pRight, pDel->_data);

			}

		}

	}
}

test.c

#include"bst.h"


void TestBST1()
{
	PBSTNode pRoot;

	int i = 0;
	int arr[] = { 5, 3, 4, 1, 7, 8, 2, 6, 0, 9 };
	int size = sizeof(arr) / sizeof(arr[0]);
   
	InitBSTree(&pRoot);
	for (; i < size;i++)
		NorInsertBSTree(&pRoot,arr[i]);

	PreOrder(&(*pRoot));

	printf("\n");

	NorDeleteBSTree(&pRoot,2);
	PreOrder(&(*pRoot));
	printf("\n");


	NorDeleteBSTree(&pRoot, 4);
	PreOrder(&(*pRoot));
	printf("\n");


	NorDeleteBSTree(&pRoot, 7);
	PreOrder(&(*pRoot));
	printf("\n");


	printf("data = %d ", NorFindBSTree(&(*pRoot), 5));

	
}


#if 0
void TestBST2()
{

	PBSTNode pRoot;

	int i = 0;
	int arr[] = { 5, 3, 4, 1, 7, 8, 2, 6, 0, 9 };
	int size = sizeof(arr) / sizeof(arr[0]);

	InitBSTree(&pRoot);
	for (; i < size; i++)
		InsertBSTree(&pRoot, arr[i]);

	PreOrder(&(*pRoot));
	printf("\n");


	DeleteBSTree(&pRoot,2);
	PreOrder(&(*pRoot));
	printf("\n");



}

#endif
int main()
{
	TestBST1();
	//TestBST2();

	system("pause");
	return 0;

}

 

二叉搜索树的初始化、插入、删除、查找、销毁等操作
Calm的博客
09-15 2471
二叉搜索树的概念 二叉搜索树又称二叉排序树，它或者是一颗空树，或者是具有以下性质的二叉树： 若它的左子树不为空，则左子树上所有结点的值都小于根结点的值 若它的右子树不为空，则右子树上所有结点的值都大于根结点的值 它的左右子树也分别为二叉搜索树 例： 我们要实现这些操作。先定义一个二叉搜索树的结构体，这个结构体成员包括左右孩子两个指针，还有它的数据： typedef int B...
C数据结构-二叉搜索树BSTree
water_3700348的博客
10-11 918
二叉搜索树BSTeee #ifndef BSTREE_H #define BSTREE_H #ifndef NULL #define NULL 0 #endif /* 元素类型 */ typedef int elem_t; /* 节点结构体 */ typedef struct tag_bstree_node { elem_t data; /
二叉搜索树
gy的博客
05-21 269
//BSTreeNode.h ​ #pragma once #include&lt;stdio.h&gt; #include&lt;stdlib.h&gt; #include&lt;assert.h&gt; #include&lt;malloc.h&gt; typedef int DataType; typedef struct BSTreeNode { struct BSTreeNode...
二叉搜索树的基本操作
zhang21722668的博客
08-31 328
完整代码块 /*************************************************/ //BSTree.h typedef int SDataType; typedef struct BSTNode { struct BSTNode *_pLeft; struct BSTNode *_pRight; SDataType _data; ...
C++实现二叉排序树BSTree --插入删除摧毁查找等操作
FreeeLinux's blog
08-11 3097
一：二叉排序树定义 二叉排序树（Binary Sort Tree）又称二叉查找树（Binary Search Tree），亦称二叉搜索树。 二叉排序树是这样一棵树： （1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值； （2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值； （3）左、右子树也分别为二叉排序树； （4）没有键值相等的结点。 二：删除算法（重点）
13、二叉搜索树：高效的数据存储与操作结构
最新发布
o0p1q2r3的博客
10-13 20
本文详细介绍了二叉搜索树（BST）作为一种高效的数据存储与操作结构，对比了其与数组和列表在插入、删除和搜索操作上的性能差异。文章讲解了二叉搜索树的基本概念、节点结构、约束条件，并通过代码示例展示了插入、搜索和删除的实现方式。同时分析了插入顺序对树结构的影响，探讨了重复值处理、空树情况及性能优化建议，并列举了其在数据库索引、文件系统和编译器中的实际应用场景。结合流程图与性能表格，帮助读者全面理解二叉搜索树的工作原理与优势。
pta数据结构二叉搜索树
12-28
这一过程不仅有助于掌握基本的操作技能，而且可以增强对数据结构内部机制的认识。 #### 寻找共同祖先问题 当面对诸如“求两个指定节点之间的最低公共祖先”的挑战时，一种有效的方法是从根向下追踪路径直至遇到任一...
C#实现二叉搜索树的基本操作与功能
二叉搜索树（Binary Search Tree，简称BST）是一种重要的数据结构，在计算机科学中广泛应用，尤其在需要高效查找、插入和删除操作的场景中表现优异。本资源标题为“C#实现二叉搜索树基本功能”，描述同样强调了使用...
基于 Python 的二叉搜索树源码.zip
08-16
二叉搜索树的基本操作包括插入、查找和删除。插入操作是指将一个新的节点按照二叉搜索树的性质插入到树中的适当位置。查找操作是指根据给定的值，在树中寻找对应的节点。删除操作则是指移除树中的某个节点，并确保树...
数据结构课程设计(二叉排序树的相关操作).pdf
09-30
设计要求涵盖了二叉排序树的基本操作，包括创建、查找、插入和删除节点，以及中序遍历输出。 在系统设计方面，设计了一个主菜单，包含多个子菜单，便于用户选择所需的操作。二叉树的节点用链式存储结构表示，每个...
20 二叉树：销毁
Ultravioletrays的博客
05-01 1645
20二叉树：销毁 作者:冯向阳时间限制:1S章节:DS:树 截止日期:2022-06-30 23:55:00 问题描述 : 目的：使用C++模板设计并逐步完善二叉树的抽象数据类型（ADT）。 内容：（1）请参照链表的ADT模板，设计二叉树并逐步完善的抽象数据类型。（由于该环境目前仅支持单文件的编译，故将所有内容都集中在一个源文件内。在实际的设计中，推荐将抽象类及对应的派生类分别放在单独的头文件中。参考教材、课件，以及网盘中的链表ADT原型文件，自行设计二叉树的ADT。） 注意：二叉树A...
[数据结构] BSTree二叉搜索树的模拟实现
Darling_sheeps的博客
11-07 567
它或者是一颗空树，或者是具有下面性质的二叉树：若它的左子树不为空，左子树的结点的值都小于根结点的值；若它的右子树不为空，右子树结点的值都大于根结点；同时，它的左右子树又都是搜索二叉树。
数据结构13.二叉搜索树 BST
Aemonair's　世界树．
08-20 791
引言　 一． 二叉搜索树定义 二．二叉树搜索的接口 三. 搜索二叉树的接口实现 四. 函数功能检测 五. 总结
bstree的插入删除函数
Faded0104的博客
07-12 546
搜索二叉树的插入函数：从根结点去寻找要插入的结点，如果值相等，则插入失败返回；如果key小于结点值则向左走，如果大于则向右走，直到按这个规则到达树叶子结点，则为插入的位置，然后new出这个结点插入． 搜索二叉树的删除：先是从根开始去寻找要删除的结点（从根遍历如果值相等的找到，如果小与则向左寻找，如果大于则向右寻找），找到后执行删除动作，分为两种大的情况： １．要删除的结点既有左边孩子又有右边孩
二叉搜索树的基本操作 ---- 插入，删除，查找，销毁，遍历
阿巴卡的博客
09-04 1039
首先来看看二叉搜索树的概念 二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值 它的左右子树也分别为二叉搜索树 二叉搜索树的结构体 #define bool int #define true 1 #define false 0 typedef ...
二叉树 BSTree 完整实现
CC_且听风吟丶的博客
11-03 1126
// 二叉查找树的实现头文件 // 二叉树的操作中有很多重载操作，分开了内部和外部的接口 #ifndef _DZZHYK_BSTREE_H_ #define _DZZHYK_BSTREE_H_ #include <iostream> #include <iomanip> using namespace std; // BST节点 template <class ...
二叉搜索树及其实现与应用
zimituanzi_的博客
06-08 2319
   首先什么是二叉搜索树？二叉搜索树又称为二叉排序树，它是一个空树或者具有以下性质：1）若它的左子树不空，则左子树上的所有节点的值都小于根节点的值2）若它的右子树不空，则右子树上的所有节点的值都大于根节点的值3）它的左右子树也分别为二叉搜索树由二叉树的定义可以看出它是递归定义的，下面是一些二叉树的基本操作的递归实现：typedef int DataType; typedef struct BST...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值