连载翻译 | 流形学习的数学基础-3核学习

深度学习的降维过程实质上是学习高维数据的流形结构，常用的卷积神经网络产生特征后，即可以接全连接神经网络，也可以用其他机器学习方法，这个过程是学习概率分布，所以说端到端的深度学习算法是模糊了这两个过程，概率分布的学习目前已经有了较多的方法，但是深度学习对流形结构的学习和降维目前的约束和认识是非常弱的，因此有必要将流行正则化框架融入到目前的深度学习框架中。

博客：

https://blog.youkuaiyun.com/weixin_38817895/article/details/110505860

推荐阅读：

连载翻译 | 流形学习的数学基础-1介绍

连载翻译 | 流形学习的数学基础-2基础

在上一章中，我们将学习问题描述为在函数H的空间上最小化含有正则化项的经验风险（误差）。

本章致力于构造一个适当的函数空间H，即再生核希尔伯特空间。我们的方法受到了[13,68,75,81]的启发。

一旦我们理解了这些空间，就会发现我们的经验风险最小化问题可以大大简化。具体来说，Representer定理3.3.1指出，它的解可以写成在我们的数据点上求值函数（核）的线性组合，使得对H的优化和对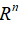的优化一样简单。

在本章的最后，我们将这些工具发展到核学习的一般框架中，并描述了三种经典的核学习算法。由于其通用性和简单性，核学习跻身于当今实践中最流行的机器学习方法之列。

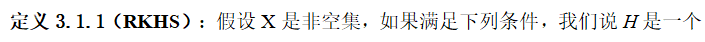
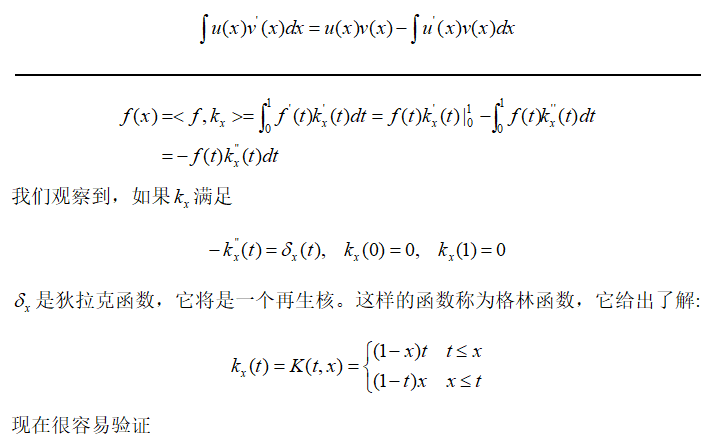
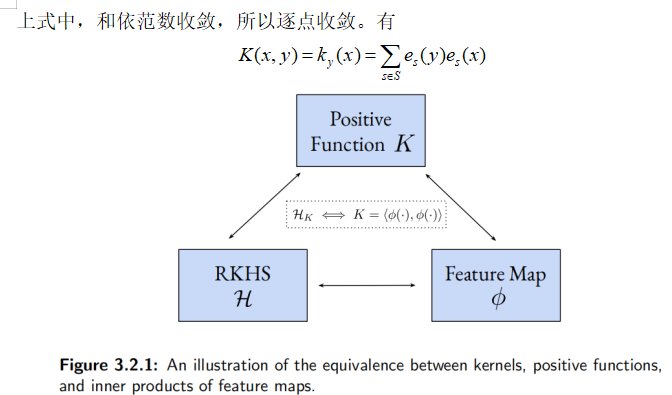
再生性指的就是原本函数之间计算内积要算无穷维的积分，也就是这个映射函数可以映射到高维甚至无穷维（高斯核），而计算无穷维的积分是很复杂的，但是现在只需要算核函数就可以。