基于GPS数据的出租车寻客推荐

出租车推荐系统：基于出租车GPS数据的寻客推荐系统

摘要

推荐系统旨在通过从海量复杂数据中获取有用知识，以在信息过载的环境中搜索用户感兴趣的内容。随着信息量和数据结构复杂度的不断增长，如何高效地处理、建模和分析信息已成为一个更具吸引力且富有挑战性的课题。由于全球定位系统（GPS）记录了出租车的行驶时间和位置，配备GPS的出租车可被视为城市交通系统的探测器。本文提出了一种基于大规模出租车轨迹数据的寻客推荐系统（Taxi‐RS），旨在为乘客提供在特定位置打到出租车的概率及等待时间。我们基于热点扫描（HotSpotScan）和偏好轨迹扫描（Preference Trajectory Scan）算法构建了离线处理系统，并提出了一种用于频繁轨迹图的新数据结构。最后，设计了一个优化的在线查询子系统，用于计算打车概率和等待时间。Taxi‐RS基于一万两千辆出租车一个月内产生的真实轨迹数据集构建。实验结果表明，在保证准确性的前提下，与朴素算法相比，本系统能够为给定位置提供更精确的等待时间预测。

索引术语

大数据、频繁轨迹图（FTG）、推荐算法、出租车全球定位系统（GPS）数据、出租车推荐系统（Taxi‐RS）

一、引言

TRAJECTORY 可以被视为移动对象随着时间变化在空间中的轨迹。轨迹数据的汇聚使得能够轻松获取使用移动设备的用户的轨迹信息[1]。全球定位系统（GPS）作为地理定位技术中日益发展的一种，被广泛应用于出租车上，使得配备GPS的出租车可被视为城市交通系统的探测器。如今可以随时获取整个城市的出租车位置信息。由于轨迹数据[3]的数量和数据结构的复杂度不断增长，如何高效地处理、建模和分析大规模移动数据已成为一个更具吸引力且富有挑战性的课题。

出租车是人们在城市中出行的重要工具，但有时人们常常会面临一种尴尬的情况：在特定地点等待出租车的时间过长。大多数人都有过这样的经历：仅仅因为你在特定地点晚到了2分钟，就不得不等待超过10分钟才能打到一辆出租车。另一个例子：你已经在街道边等了超过15分钟，但你的邻居刚从家出来，穿过街道，走了几米就立刻打到了出租车。看起来，人们需要获取更多信息才能打到车，而不是长时间地无助等待。随着出租车数量的增加，利用大规模出租车GPS数据来求解推荐位置信息并计算等待时间变得愈发紧迫。

在信息时代，收集信息变得非常容易。对于上述出租车问题，利用大规模出租车GPS数据来推荐位置信息并计算等待时间成为一个非常有趣的问题。

本文提出了一种基于大数据环境的出租车GPS历史数据处理方法，包括离线处理和在线处理。我们实现了一个名为寻客推荐系统（Taxi‐RS）的推荐系统，该系统能够在给定时间和地点信息的情况下，计算出打到出租车的概率和时间。以下是本文的主要内容。

1) 我们设计了数据的离线处理。首先，我们设计了一种称为热点扫描（HSS）算法的算法，用于扫描城市中的热点区域。然后，通过一种称为PTScan（Preference Trajectory Scan）的新算法识别出租车偏好轨迹。
2) 我们基于出租车偏好轨迹提出了一种离线图模型，并利用多重邻接表存储离线压缩数据。
3) 我们利用离线模型构建了一个概率模型，用于计算打到出租车的概率和等待时间，并分析了在线处理的复杂度。

本文的其余部分组织如下。第二节对相关文献进行了简要回顾。第三节正式介绍了一些概念。第四节给出了出租车推荐系统（Taxi‐RS）的概述。第五节介绍了离线处理的关键算法。第六节提出了频繁轨迹图（FTG）模型。第七节提出了一种计算模型以获得出租车乘坐服务。第八节给出了实验评估的结果。第九节在结论部分提出了若干备注。

II. 相关工作

城市交通流是分析城市实时交通状况的重要工具[4],[12]。近年来，在全球定位系统交通数据分析和处理技术方面已有一些相应的工作。一些研究专注于路线规划，而另一些则致力于帮助出租车司机寻找最近的乘客或最大化司机收入。

A. 轨迹挖掘

为了进行乘客寻觅推荐，利用从历史轨迹中发现的知识是一个重要的应用。解决该问题的传统方法是识别兴趣地点。Zheng et al.[7]提出了几种从GPS数据中学习交通模式的新方法。T‐Drive[6]系统是一种智能路线规划系统，通过配备全球定位系统传感器的出租车感知交通流量，并为普通用户设计最快行驶路线。T‐Drive[6]提出了一种基于时变地标图的路径规划算法。根据出租车轨迹数据，T‐Drive可以利用虚拟边学习细微的时间成本。T‐Drive的一个改进版本[7]考虑了更多因素，包括天气、个人驾驶习惯、技能以及其他因素。T‐Finder系统[8],[9]推荐出租车最有可能载到乘客的地点。该系统使用聚类算法从出租车轨迹中找出司机可以获得更高收入的位置，然后利用概率模型分析司机和乘客在选择不同策略时的成本与风险。另一个乘客寻觅系统是HUNTS[21]。HUNTS系统为出租车司机提供寻客轨迹推荐，以提高其收益。

B. 路径规划

路线规划可分为个性化路线规划和动态路线规划。从推荐的角度来看，路线规划包括出租车寻客推荐、节能驾驶路线推荐、快速驾驶路线推荐等。根据所考虑轨迹的范围，路线规划算法可分为全局算法和局部算法。局部算法也称为增量算法，其通过贪心策略将每个轨迹点匹配到合适的路段。这类算法通常基于距离和角度的相似性[18]–[20]，为每个轨迹点寻找局部最优的匹配路段。另一方面，全局算法的考虑对象通常是完整的轨迹，其目标是找到在某种意义上最接近轨迹的道路序列。近年来，一些研究采用弗雷歇距离[16]和弱弗雷歇距离来比较轨迹之间的相似性[17]。

然而，以往的研究通常从司机的角度考虑推荐系统，明显忽略了乘客的需求。我们认为，当一个人在等待出租车时，有必要回答以下几个问题：在当前位置是否容易打到出租车？第一辆空车出租车到达当前位置需要多长时间？最近的“最佳打车地点”在哪里？在那里等待需要多久？本文中，我们引入一种新技术——出租车寻觅（taxi hunting），以回答上述问题。

III. 问题定义

本文中，我们利用出租车GPS设备产生的大规模数据求解以下两个问题：1）计算在特定时间和地点打到出租车的概率；2）计算直到第一辆空车出租车满足需求为止的等待时间。以下是一些基本定义。

A. 基本定义

假设有 n 辆出租车，即 Taxi={Taxi1,…,Taxin}。每一条 GPS 数据称为一个 GPS 数据点。此处，我们给出更详细的定义[5]。

定义 1. GPS数据点 ：一个GPS数据点记录了 longitudei,j, latitudei,j、速度vi,j、方向diri,j以及运行状态State-runi,j等信息，记作gpsi,j，由一辆带有全球定位系统设备的出租车 Taxi i在时间 tj生成。即
$$ gpsi,j={Taxi i, tj, longitudei,j, latitudei,j, vi,j, diri,j, State-runi,j}. $$
(1)

某一时刻的地图由该时间的GPS数据及相应出租车的速度向量组成。地图差异可用于区分不同时刻地图之间的差异，从而高效存储大数据。因此，地图差异的精度仅影响文件块的数量，其精度程度对最终结果没有影响，仅对文件块产生轻微影响。

定义 2. 地图差异 ：给定一个时间 ti，Mapi 表示 ti 上的地图，Ri 表示 Mapi的特征值。那么，Map1 和 Map2 之间的差异 ΔMap(t2, t1) 可以定义为
$$ ΔMap(t2, t1)= Map2 − Map1. $$
(2)

类似地，Map1和Map2之间的特征值差异可定义如下（Ri的具体计算方法见第五节-A）：
$$ ΔR(t2, t1)= R2 − R1. $$
(3)

定义3. 频繁曲面 ：频繁曲面是三维曲面，定义为 TCM(x, y, z)，其中 x表示经度，y表示纬度。然后我们将 z定义为 z= count(x, y)，表示在 Point(x, y)上的出租车流量数量。某些位置具有大量的出租车流量，我们将这些点称为热点。同时，某些区域也具有大量的出租车流量，这些区域被称为热点区域。每个热点是最小不可分割热点区域。定义热点的一种方法如下。

定义4. 热点区域 ：对于地图上的每个全球定位系统 coordinates(x, y)，x 表示经度，y 表示纬度。如果一天内经过该点的出租车数量大于阈值 K，则称该点为热点区域，记为 HotSpot(x, y)。根据定义3，热点区域可用集合表示为
$$ (x, y)|z= count(x, y) ≥ K. $$
(4)

定义5. 热点区域 ：热点区域将相邻的热点区域聚集在一起；同时，相邻热点区域的 count(x, y)相似。选择一个热点 HotSpot(x, y)来代表该热点区域，记为HotSpotZone(x, y)。我们可以通过使用GPS数据计算出租车的行驶轨迹。因此，从GPS数据中获取出租车轨迹是准确且可行的。基于此，我们进行如下抽象：首先，根据每辆出租车的标识区分出租车轨迹，即每辆出租车都有其独立的路径，这些轨迹彼此相互独立；其次，轨迹是出租车行驶的歷史数据。如果存在一条轨迹，则表明某辆出租车在某一时刻必定经过该路线从而形成该轨迹。接下来介绍轨迹的定义，并给出相关符号说明。

定义6. 轨迹 ：出租车轨迹 Tr是指 Taxii在某一时间段内（从 tj到 tk）的行驶路径，由全球定位系统数据(gpsi,j,…,gpsi,k)表示。我们使用gpsi,j,…, gpsi,k来展示 Taxii在该时间段内的轨迹。因此，所有轨迹构成一个轨迹集合。利用轨迹表示法，频繁轨迹的形式化定义可如下方便地给出。

定义 7. 频繁轨迹 ：若一条轨迹的出现次数记为 count(Tr)，频繁轨迹是指出现次数大于指定阈值 FT的轨迹。即
$$ FrequentTrajectory|Tr: count(Tr)> FT. $$
(5)

定义8. 频繁轨迹图 ：假设我们有一组热点区域hs1,…, hsk。热点数据库用有向图 G= V, E表示。热点区域的集合 V表示所有热点区域，即 V=hs1,…, hsk。E是所有边的集合。规定从 hsi到 hsj的一条边eij表示热点区域 hsj是热点区域 hsi的后继。

B. 问题定义

总的来说，本文的寻客问题是一个局部最优轨迹检索问题，即计算在特定时间和地点成功打到出租车的等待时间。该问题的形式化定义如问题定义1所示。

1) 问题定义1 ：首辆空车到达时间(ATFC)：给定一个城市的 大规模GPS数据，找出在 时间 t，于 m分钟内，首辆 空车出租车 到达 Point(x, y) 的 等待时间 T(x, y, t, m)，其中 x 表示 经度，y 表示 纬度，m 表示 等待时间。

ATFC是指乘客在特定时间和地点成功打到出租车的等待时间。为了计算ATFC，我们需要获得打到出租车的概率（PGTR）；因此，我们定义了打到出租车的概率问题，如问题定义2所示。

2) 问题定义 2 ：PGTR：给定一个城市的出租车大规模GPS数据，求在某一时间 t，一辆出租车在 m分钟内到达特定位置 Point(x, y)的概率 P(x, y, t, m)。

为了解决这两个问题，我们给出了有效轨迹的定义。有效轨迹指的是存在如下情况的轨迹：

)

至少有一辆出租车在当前查询时间对应的过去时间段内运行。

定义9. 有效轨迹 ：假设在历史时间段内经过该点的出租车集合表示为Taxii，…，Taxij。有效轨迹是指这些出租车在[t, t+ m]的历史时间段内通过 Point(x, y)时所行驶的出租车轨迹集合，如
$$ Trvalid:{gps(u,t)→ gps(u,(t+1))→…→ gps(u,(t+m)), u ∈[i, j]}. $$
(6)

有效轨迹有一个重要特征。如果一条有效轨迹覆盖了查询时间对应的历史时间内打到出租车的地点，那么在此时刻该点的PGTR成功率会较高。我们可以通过有效轨迹的定义来给出无效轨迹的定义。在动态查询过程中，无效轨迹对查询没有意义。

定义10. ETG ：有效轨迹图（ETG）是由出租车有效轨迹组成的图，这些出租车在历史 time[t, t+m]期间曾经过 Point(x, y)。ETG G(V, E)是 FTG的子图。例如，我们可以生成一个FTG，如图1所示。

IV. 出租车推荐系统概述

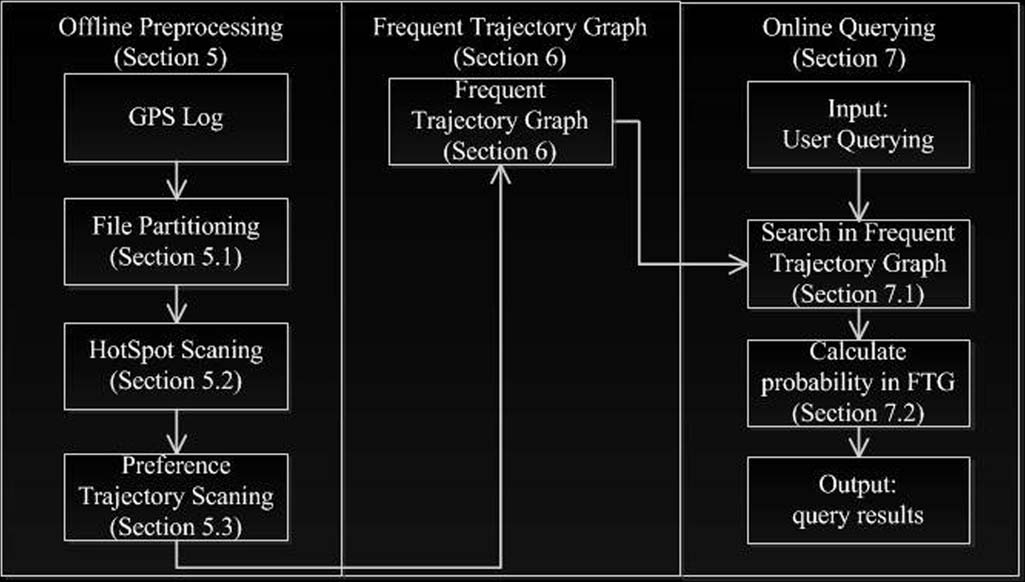
本文的核心思想是压缩和转换大规模GPS数据，以获得用于动态查询的离线模型。在每次动态查询处理中，我们使用离线模型计算等待时间和PGTR。出租车推荐系统分为三个模块：离线预处理模型、FTG模型和在线处理模型，如图2所示。

1) 离线预处理部分基于全球定位系统大数据获取离线模型训练。
2) 第二部分是获取频繁轨迹模型，用于在线查询。
3) 对于每个查询输入，搜索频繁轨迹图模型，以计算概率和等待时间。

V. 离线预处理算法

本节介绍离线预处理，包括三个阶段：文件划分、热点扫描和偏好轨迹扫描（见第五节第V-A–C节）。处理流程如下。

A. 文件分割

首先，我们读取原始的GPS数据，并将其按天划分为七个部分，因为一周有七天。考虑到出租车运行的连续性，相邻时间段之间的数据差异相较于整个时间段的所有数据而言更小。

然而，一天的数据文件过大，难以处理。我们通过以下两个步骤来解决此问题。首先，我们将一段时间内的全部 GPS数据进行存储，例如1分钟。然后，通过差异方法存储下一个时间段的数据。因此，我们认为划分文件的合适时间周期为24小时。为了计算时间 t1和 t2之间的地图差异，我们需要通过公式(7)计算一个地图特征值。假设
$$ Taxi={Taxi1,…,Taxin} $$
是由GPS数据得到的集合。为了定义地图 Mapi特征的 Ri，需要考虑两个关键特征：1）每辆出租车在时间 ti的全球定位系统位置 Point（x, y）；2）每辆出租车在ti时的速度。在给出 Ri的正式定义之前，我们先定义若干中间变量。

1) Loxi（单位：米）表示 Taxix在时间 ti的位置的经度，该值被转换为参考点的横向距离（参见第五节-B关于转换处理）。
2) Laxi（单位：米）表示Taxix在时间 ti的位置的纬度，该值被转换为参考点的纵向距离（参见第五节-B关于转换处理）。
3) Sxi表示 Taxix在时间 ti的位置与参考点之间的相对距离，定义为
$$ Sxi = \sqrt{\Delta Lo^2 xi + \Delta La^2 xi} $$
4) vxi表示 Taxix在时间 ti对应全球定位系统数据的速度（单位：米每秒）。
5) SETi 表示在时间 ti 的所有全球定位系统数据的集合。

Ri的定义由
$$ Ri = \frac{\sum_{gpsxi \in SETi} (Sxi \times vxi)}{|SETi|} $$
(7)

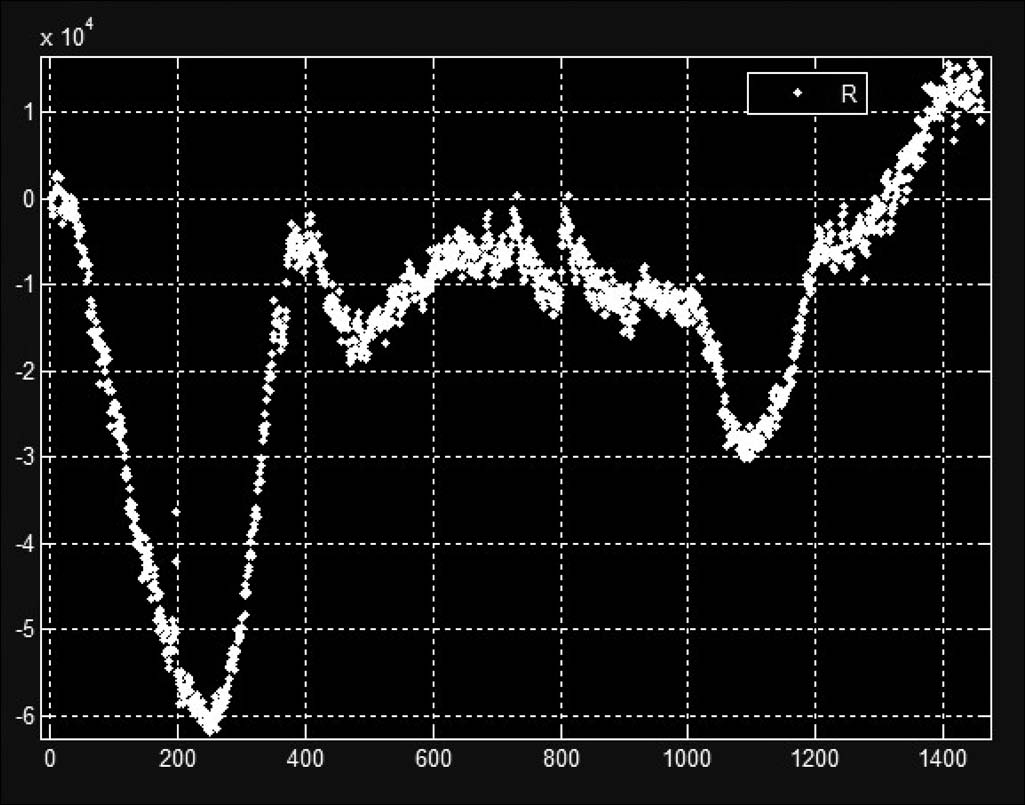
Ri可以被视为在时间 ti时行驶中的出租车位置与参考位置之间的相对距离之和。Ri可用于表示在时刻 ti城市中出租车的交通状况。图3显示了2012年11月30日每分钟的地图特征值。然后，将一天的数据文件分为四个部分。

B. 热点扫描

由于出租车轨迹可以抽象为由出租车的时间和地点拼接而成的模式字符串，因此我们可以通过选择热点区域来压缩模式字符串。有必要找出热点区域。因此，当每辆出租车的数据点映射到热点区域时，我们可以得到所有轨迹的模式字符串。

我们扫描每个文件块中的每个热点区域，以生成频繁曲面 TCM(x, y, z)，如定义3所述。因此，我们可以通过简单的哈希函数来加速访问速度。我们可以使用算法1来获取频繁曲面（如图1所示）。

算法1。生成频繁曲面。
一天中的所有GPS数据 gps1,…, gpsn
z= count(x, y) 在 TCM(x, y, z) 中。
1) 对于 i= 0 到 GPS数据数量 count[i]= 0;
2) 对于 i= 0 到 GPS数据数量
x= gps.latitude[i] × 111.7 × 1000/10
y= gps.longitude[i] × 111.7 × cos(39.5/180) × 1000/10
hash= x × 100000+ y
count[hash]= count[hash]+ 1
3) z= count;
4) 返回 z。

然后，我们会发现出现的点构成了主要道路。一些道路特别密集，而一些地方则非常稀疏。因此，形成了热点区域和热点区域存在于现实中。因此，我们提出HSS算法，通过聚合热点区域来简化计算。同时，为了确保计算精度，我们将给出阈值 k。对于曲面 z= count(x, y)= K，将地图划分为多个热点区域。类似地，我们可以通过 k= 0得到多个热点区域，即 z= 0。通常，count(x, y)= K可以保证属于 x−y平面的区域为一条闭合曲线。该闭合曲线内的所有点均为GPS数据的高频点。因此，我们已完成对热点区域和热点区域的初步筛选。

我们采用自适应划分的思想来实现热点扫描算法。我们定义一个变量 F作为阈值 K，该阈值大于(count(x, y))。

算法 2. HSS算法.
频繁曲面 TCM(x, y, z)，F=(count(x, y))，线程锁 Lock。输出：热点区域的数量，每个热点区域的代表点，每个热点区域的范围。
1) 如果(N大于 10^5)或(F等于0)则返回；
2) sub_TCM[4]=简单划分(TCM)；//4个子块按象限编号划分。
3) F= F/4；
4) 对于 i= 0到3执行 Ci= sumcount(sub_TCMi)；
5) 移除 TCM；
6) N= N −1；
7) 对于 i= 0到3，如果 Ci不远小于 F，则添加 sub_TCMi，执行hot-spot-scan(sub_TCMi, F, Lock)N= N+ 1。

HSS算法是一种递归划分过程；同时，它也包含了广度优先搜索的思想。在递归过程中，我们维护 N的值，即划分出的热点区域数量。因此，一个递归边界条件是热点区域的数量大于10^5 ，或者当前热点区域数量大于F=∑（count(x, y)）= 0（第1行）。

在递归的每一步中，当前频率曲面被均等地划分为四个部分：左上、右上、左下和右下（第2行）；同时，当前阈值 F被设为原来的1/4（第3行）。我们对每个子曲面得到(count(x,y))（第4行），并且该 SUM_count过程通过经典的数据结构——区间树进行优化。因此，我们移除了 TCM步骤以及 N减1的操作（将会有一个更小的范围 TCM来替代原来的TCM；我们在附录中证明其有效性）。然后，我们遍历四个子块，保存 TCM中不小于 F的 count(x, y)。N加1，算法进入下一层递归。同时，我们将递归计算 sub_TCM，直到所有子曲面都被划分完毕。类似地，我们可以证明HSS算法的正确性，即其递归边界的可达性。

C. 偏好轨迹扫描

经过热点扫描后，初始GPS数据的规模将大大减少，但所选数据对于最终解决方案而言仍然过大。我们注意到以下现象。

1) 出租车司机通常在几条固定的街道上找到乘客。
2) 很少有轨迹是偶然发生的。例如，乘客的目的地比较特殊，司机在返回时不得不经过这条路线。
3) 有时，出租车司机会因为某些特殊因素而经过特定的路线。

前面提到的三种情况在现实生活中非常常见且频繁发生。然而，这些情况对推荐出租车的结果有很大影响。推荐算法应基于更频繁和更普遍的轨迹。因此，我们应关注案例1中提到的轨迹，同时尽量排除案例2和案例3中提到的轨迹。在现实生活中，一些司机偏好某些路线；换句话说，路线的选择具有偏好性。出租车的行驶轨迹可视为与时间相关的序列。因此，偏好路线的轨迹必然是频繁出现的。在频繁轨迹上有大量可用出租车；因此，我们可以确保在合理时间内有可用出租车到达某个位置。为了识别偏好轨迹，我们需要在关键点识别出租车的轨迹。

由于在离线处理中使用了历史数据，我们采用 PrefixSpan算法的思想[10] 扫描全球定位系统历史数据，以找出频繁出现的子串。我们将该算法称为PTScan。

PTScan算法通过过滤不频繁的序列，从候选序列中选择频繁序列。根据我们的实验，频繁轨迹的阈值为10。

这里，我们给出PTScan算法的一些符号。符号 ω表示一个时间段内的出租车轨迹，可视为一个序列。符号 S表示 ω的一个子串。符号 S|ω表示 ω在S上的投影。特别地，如果 ω为空，则 S|ω为 S。

算法3. PTScan算法.
全球定位系统历史数据，ω。输出：频繁子串。
1) 扫描 S|ω，找到序列b满足 length(b)= 1；
2) 将序列 b添加到 ω的末尾形成新序列。
3) < b>可作为 ω的最后一个元素并构成序列。
4) 对于每个序列 b，将 b加入 ω以形成序列ω，并输出 ω。
5) 对于每个 ω，构建其投影数据库 S|ω，并调用算法 PTScan(ω, length(ω)+ 1, S|ω)。

基本上，PTScan算法的工作流程如下。首先，我们扫描出租车轨迹序列数据库，生成所有长度为1的序列。然后，进行相应的投影数据库是根据长度为1的序列形成的。因此，我们在相应的投影数据库上重复之前的步骤，直到不再生成长度为1的序列为止。最后，我们对每个不同的投影数据库重复该过程，直到不再产生新的长度为1的序列。

PTScan算法通过使用分治思想，持续将轨迹序列数据库生成多个更小的投影数据库。然后，该算法在每个投影数据库上挖掘序列模式，以获得出租车驾驶偏好轨迹。PTScan算法侧重于可用出租车的序列模式。

VI. 频繁轨迹图

本部分介绍如何设计频繁轨迹图模型以及如何构建频繁轨迹模型的存储和相关数据结构。我们根据离线预处理结果获取出租车轨迹的频繁模式子串。由于本文的关键是求解在查询点 m分钟内能够搭乘到出租车的概率，因此需要分析并构建影响最终求解概率的相关因素。

如果一辆可用的出租车在 m分钟内到达指定位置，我们必须确保以下条件。

1) 为了确保有可用的出租车能在 m分钟内到达某个位置，我们需要根据历史数据来分析速度和距离。
2) 为了确保当出租车在前往途中时不会被其他人叫走，我们需要分析历史数据中的触发条件，并计算各个方向上途中其他人的PGTR。
3) 为了确保查询位置位于首选路径上，因此我们构建了频繁轨迹图。

对于频繁轨迹图 FTG=(V, E) 中的查询时间 t0，提出了两个符号 w(V) 和 w(Ei,j)。w(Vi)= n 表示在时刻[t0 − m, t0]聚合点 Vi内可用出租车的总数。w(Ei,j)=(P,T)表示由 P 和 T组成的两个元组。P 表示出租车在 m分钟内从 Pointi行驶到 Pointj 的概率。T表示出租车从 Pointi 到 Pointj 的行驶时间。

构建FTG并不复杂。然而，FTG将包含 |V| = N ≈ 10^5个节点，并近似于一个完全图；因此， |E| ≈ |V|^2 ≈ 10^10。如果仅使用经典的邻接矩阵和邻接表来存储FTG ，将会产生过大而无法接受的空间开销。例如，邻接矩阵的空间复杂度为 O(|V|^2)，邻接表的空间复杂度为O(E)。我们在查询时引入了有效轨迹的概念，从而使新数据结构能够按时间分层。因此，我们设计了如图4所示的新数据结构，以减少空间开销。在新数据结构中，我们使用 n表示一个 10 m ×10 m热点区域的统计频率，按从最稀疏区域到最密集区域的升序排列。实际上，热点区域存在大量重复频率，因此仅有 10^5个不同的值。我们使用 t表示从0到24小时的时间，按每分钟分层，便于查询。

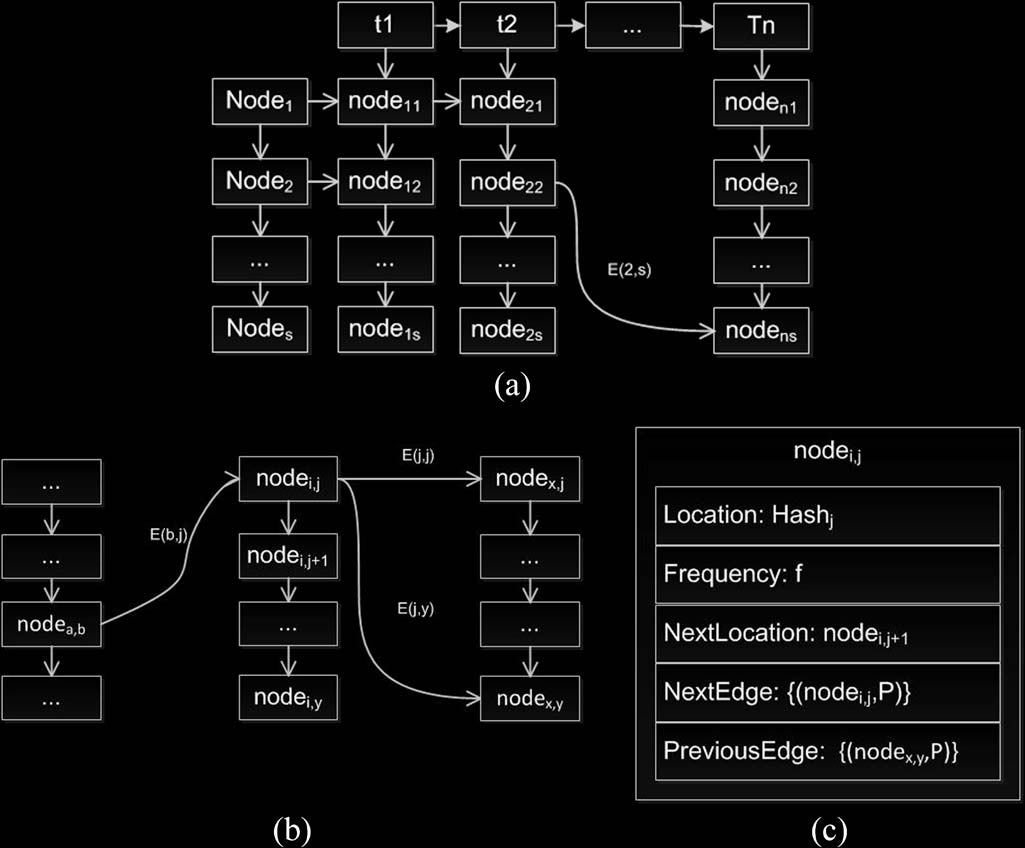时间分层多重邻接表（TMAT）。(b) nodei,j，前驱节点：nodea,b，以及后继节点：nodex。(c) 节点 nodei,j 的数据结构图)

在图4(a)中，ti指向当前时间所有划分出的热点区域的情况，并将每分钟的地图划分为约 N ≈ 10^5个热点区域。热点区域的哈希值是唯一标识的。数据结构中的每个热点区域表示为nodei,j。nodei,j表示在Hash= j的 ti时间上的热点区域。该数据结构称为时间分层多重邻接表（TMAT）。

假设nodei,j表示时间 ti下节点 Vj，nodex,y表示时间 tx下节点 Vy。如图4(b)所示，E(j, y)表示图模型中 nodei,j与nodex,y之间的边关系，w(Ej,y)表示两个元组(P, T)，且这两个值已经计算得出。此外，我们不需要单独存储 w(Ej,y).T，因为它可以通过数据结构直接计算得到（w(Ej,y).T= tx − ti）。我们只需存储 w(Ej,y).P即可。

因此，可以将其映射为由PTScan算法获得的热点轨迹字符串的多重邻接表。同时，我们更新TMAT中的边信息。例如，对于边nodei,j→ nodex,j，如果位置随着时间保持不变，则反映了出租车的停车状态。

每个节点的数据结构如图4(c)所示nodei, j。以下是对应该数据的说明nodei, j。

位置：Hash j 表示由node i, j代表的具体热点区域位置，通过之前计算的哈希值表示。
频率：f表示node i, j在时刻 ti的车辆频率。
下一位置：node i, j +1表示 node i, j在时刻 ti的下一个相邻节点 node i, j +1。
下一边：node x, y , P表示车辆node i, j在频繁模式子串中时刻 ti 之后的后续节点（图5中的关系）及其对应的权重 P。
前一时刻：node a,b, P表示车辆node i, j 在频繁模式子串中的前驱节点（边图5中的关系以及它们在 ti时刻之前的相应权重 P。

对于TMAT，我们分别计算并存储了两个文件（工作日离线模型和周末离线模型）。此外，在后续查询中，我们可以读取指定日期的对应的数据结构文件。

VII. 在线查询算法

这里，我们介绍一种基于离线模型的动态在线处理算法。首先，我们可以获得查询的以下信息： 1) 我们想要搭乘出租车的地点（x, y），由GPS坐标表示；2) 查询时间；3) 查询可接受的等待时间 m。

对于一个查询点，我们找出会影响PGTR的可疑点。同时，我们还通过训练现有的大规模数据得到了一个频繁轨迹图。这些问题可以动态求解。首先，我们根据GPS坐标在离线图模型上定位热点区域；接下来，我们在可能影响PGTR的热点区域周围寻找可疑热点。核心思想是搜索过程。在线查询部分如下。

1) 将查询位置 Point(x, y) 定位到相应的热点区域。
2) 根据时间信息 t 找出可能到达查询点 Point(x, y) 的轨迹数量（见第七节A部分）。
3) 根据 m 分钟内的轨迹数量，估计打到出租车的概率建模中的参数。计算打到出租车的概率和等待时间（见第七节B部分）。

获得离线模型后，我们通过TMAT表的索引进行快速查询。首先，将用户的查询位置 Point(x, y) 定位到离线模型中的相应热点区域；其次，根据查询时间 t，找出在 [t, t+ m]期间经过 Point(x, y)的轨迹数量。然后，在分析后该概率符合泊松分布，因此我们可以根据轨迹数量估计泊松分布的参数。最后，通过泊松分布计算PGTR分布，并根据几何分布计算等待时间。总之，在线查询速度非常快。

A. 两个问题的解决方案

这里，P表示出租车从点Pointi驶向 Pointj的 m分钟内的概率。T表示出租车从点 Pointi驶向 Pointj的时间。求解 P和 T的方法如下。

1) 求解 P的方法 。P 的影响因素包括出租车驾驶偏好和途中叫到出租车的状况。

a) 对于出租车驾驶偏好：针对所有热门字符串，我们统计V′i的出现次数 ni。V′j作为 V′i的直接后继的出现次数为 ni，如图所示
$$ Pi,j(preference)= \frac{ni}{nj}. $$
(8)

b) For the condition of getting a taxi ride during the way: The events of getting a taxi ride are independent of each other; hence, all events that the relevant taxis are being ridden are independent and identically distributed. Suppose that pk represents the PGTR on its way. pk can be calculated using
$$ Pi,j(non-get)= 1 − \prod_{k∈Ei,j}(1 − pk). $$
(9)

P 可通过以下方式计算
$$ Pi,j= Pi,j(preference) × Pi,j(non-get). $$
(10)

2) 求解 T的方法 。
假设有两个热点区域Vi和 Vj。假设S表示从 Vi到 Vj的平均行驶距离。假设 H表示从 Vi到 Vj的平均速度。那么，我们可以通过方程T= S/H计算从 Vi到 Vj的行驶时间。

B. 优化过程

所有历史数据均已映射到新数据结构，即TMAT图上；然后通过搜索该图的策略来求解问题。对于每个查询点（用位置坐标表示），我们应搜索其对应的热点区域。接着，我们沿相反方向搜索所有指向该热点区域的边。因此，在搜索图[13]–[15]的过程中可以得到一棵查询树。查询位置是该树的根，而TMAT图上相关的热点区域则是叶子的枝叶。

在搜索过程中，我们维护两个值。对于起始点，我们定义了一个剪枝优化参数 θ和一个搜索边界 μ。最初，μ= m。当进入一个新的搜索层时，μ减去 w(E).T(μ= μ − w(E).T)。同时，搜索边界将由 μ确定。（显然，边界应该是 μ= 0。我们可以认为出租车在 m分钟的时间限制内从查询位置行驶到周围位置。）另一方面，θ是在从叶节点向上合并到根节点的过程中获得的。

搜索树。对于父子关系参数θ，我们使用乘法运算。兄弟关系的参数通过以下方式计算
$$ θ= 1 − \prod_{i=0}^{m}(1 − w(E).P). $$
(11)

同时，我们使用剪枝优化参数βi对搜索优化进行剪枝。在搜索第 i层时，当前层所有概率的一侧是集合 PSi={w(E)Pi0, w(E).Pi1,…, w(E).Pim}，我们将其量级定义为 βi。然后，βi通过以下方式计算
$$ βi= \lg\left( \frac{\sum_{p∈PSi} \lg(w(E).P)}{|PSi|} \right). $$
(12)

βi的含义是第 i层的概率的平均位数。例如，如果 βi= −2，则表示当前层的平均概率水平为0.01。当搜索到第 j层时，我们会发现该层的概率是各层之间关系的乘积以及概率 p ∈[0, 1]的结果。因此，当搜索深度足够深时，该层的概率对总体概率的影响很小。尽管在搜索过程中 μ尚未达到其边界，但这种搜索已无意义，因此需要进行剪枝。在第 i层搜索时，αi将被更新
$$ αi= \sum_{i=0}^{n} βi. $$
(13)

公式(13) 表示在搜索到达当前层时当前概率的量级。显然，如果 αi βi，则应进行剪枝。如果 αi − βi< −5，由于我们在过程中取了对数，可将其视为 αi βi。

在搜索过程中，我们发现这两种搜索方法可能相似甚至相同。因此，我们记录搜索结果并采用记忆化搜索的方法，以加快搜索过程。同时，我们希望添加一个新的离线文件。给定一个查询位置，我们首先查询离线文件以检查该位置是否在之前的查询中已被查询过。如果该查询位置尚未被查询过，则不会在树上进行搜索。

算法4。用于优化的搜索与剪枝算法 [SPO算法 (μ, β)]

(1) 出租车位置 (x, y)，由全球定位系统坐标表示，并将查询转换为相应的热点区域；
(2) 查询时间 t；
(3) 查询可接受的等待时间 m
(4) 搜索过程中的剪枝优化参数 λ和剩余时间 μ；
(5) 全局参数 α和 对β。于此查询，经过查询位置的总概率和出租车总数。（在每层搜索中，我们存储每条边上的概率和耗时。）

1) 如果 μ不大于0
a) 保存(β, m− μ
b) N= N+ M × β //N：表示能够到达查询位置的出租车总数，M表示能够从查询位置搜索到的出租车总数
c) return 0
2) if β less than α −5
a) save(β, m− μ)
b) N= N+ M × β
c) return 0
3) p= 1
4) for e in adjective E
a) p= p ×(1 − SPO(μ − w(e).T, β ∗ w(e).P))
5) return 1 −p

总之，SPO算法在搜索过程中包含了剪枝优化。它通过使用记忆化搜索来提高搜索效率。

C. 两个问题的计算过程

使用SPO算法，我们可以计算从所有可能的点到达的出租车数量，这等于预期的出租车数量。对于此问题，PGTR与泊松概率分布一致。对于特定的时间和特定的位置，概率分布函数为
$$ P(x= k)= \frac{e^{−λ}·λ^k}{k!}. $$
(14)

公式(14)中的参数 λ是随机事件在单位时间（或单位面积）内发生的平均概率。因此，泊松分布适用于描述单位时间内随机事件发生次数的情况。通常，泊松分布的数学期望用 E(P(λ)) = λ表示，对于当前问题为P(λ)。我们可以得到泊松分布系数。因此，能够搭乘出租车的概率为
$$ P= P(x= 0)= \lim_{(n→∞)} \sum_{i=1}^{m} P(x= i)= 1 − e^{−λ}. $$
(15)

同时，第一辆出租车到达的时间服从几何分布；因此，我们可以通过以下过程计算该时间。

首先，对于查询点的所有相邻边，我们可以获得到达相应边的平均时间。然后，通过将平均时间 Timei 按升序排序，可以得到一系列元组(P1 , Time1) ,(P2 , Time2) …, (Pn , Timen)。（Timei 按升序排列，我们可以通过此方式获得元组序列）

早期搜索算法。）为了计算等待所用的时间，我们可以使用
$$ T= P1Time1+(1 − P1)P2Time2+(1 − P1)(1 − P2)P3Time3+ · · · + \prod_{i=1}^{n−1}(1 − Pi)PnTimen. $$
(16)

在线处理算法已完成。总之，对于特定位置(x, y)，在某一时间段 ti内，m分钟内的PGTR受到参数 λ的影响，该参数表示在 m分钟内到达的出租车数量。等待时间则受由(16)中的 P和T构成的元组影响。

VIII. 实验

这里将展示使用真实数据库进行实验评估的结果。

A. 实验数据集和实验平台

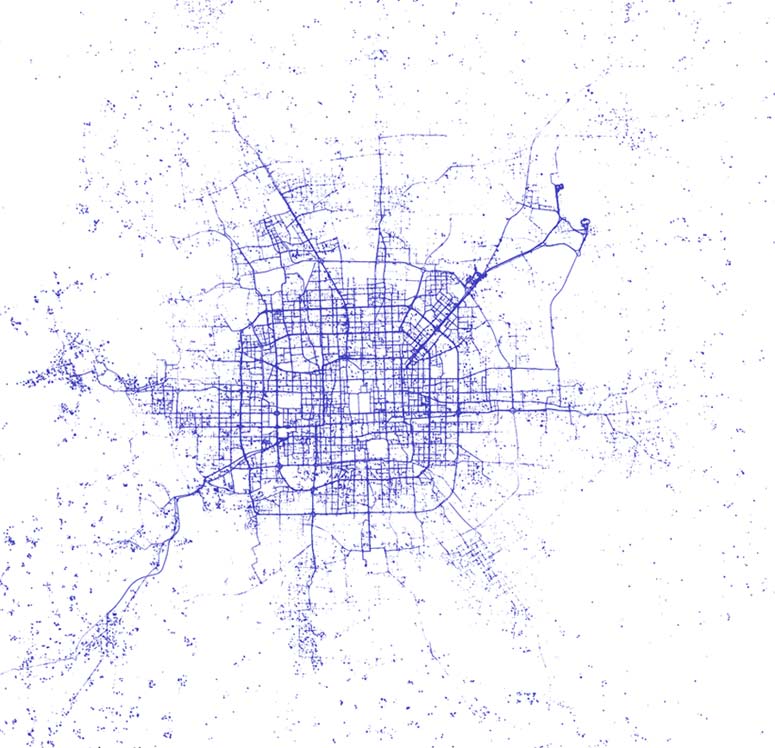
我们基于北京市12000多辆出租车一个月内产生的真实数据集构建系统。该数据集包含约11亿条全球定位系统数据，每天的数据量约为3000万条，大小为2‐G。该数据集记录了出租车的轨迹。本文的离线预处理和频繁轨迹构建在 Hadoop平台上进行。

1) 离线处理分析 ：离线处理的大部分时间消耗在信息处理方法上。离线处理总共仅耗时5小时。由于对于给定的数据，采用了一种递归操作（10^9）O(n)，离线处理的最大复杂度为 O(nlog n)。其他算法为 O(εn)。对于离线处理，我们进行了良好的优化。

2) 在线处理分析 ：构建一天内的频繁轨迹需要花费20分钟。在线处理使用包含热点轨迹信息和频繁统计的频繁轨迹图（FTG）。这种存储方法相比通用图模型（如邻接表）可以节省更多空间。尽管离线结果的最终存储空间需要5.5 GB，但这是为确保准确性所不可避免的。

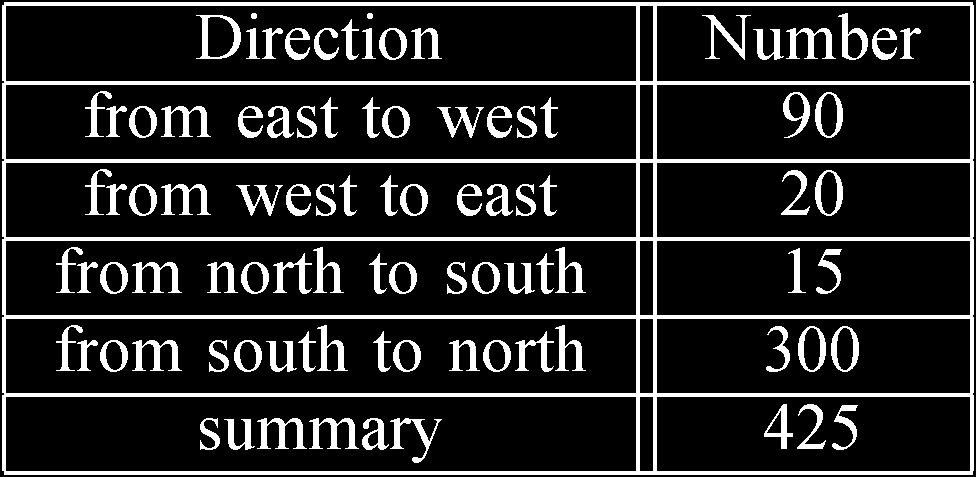
3) 模型耗时分析 每次在线查询可在约0.5秒内完成，因为相关数据已被压缩存储。这得益于算法1中搜索优化剪枝（SPO算法）和原始哈希处理的过程。经过上述处理后，搜索深度较小。在成功计算PGTR时搜索深度为3，在计算等待时间时为15。当概率小于0.001 （p< 0.001）时，我们会对查询点的搜索树进行剪枝。因此，平均搜索深度为5。结合记忆化技术（动态规划），时间复杂度接近于线性计算。每个方向的测试次数统计见表I。

表I 每个方向的统计测试点数量

方向	测试点数量
从东到西	108
从西到东	105
从北到南	107
从南到北	105

B. 实验结果

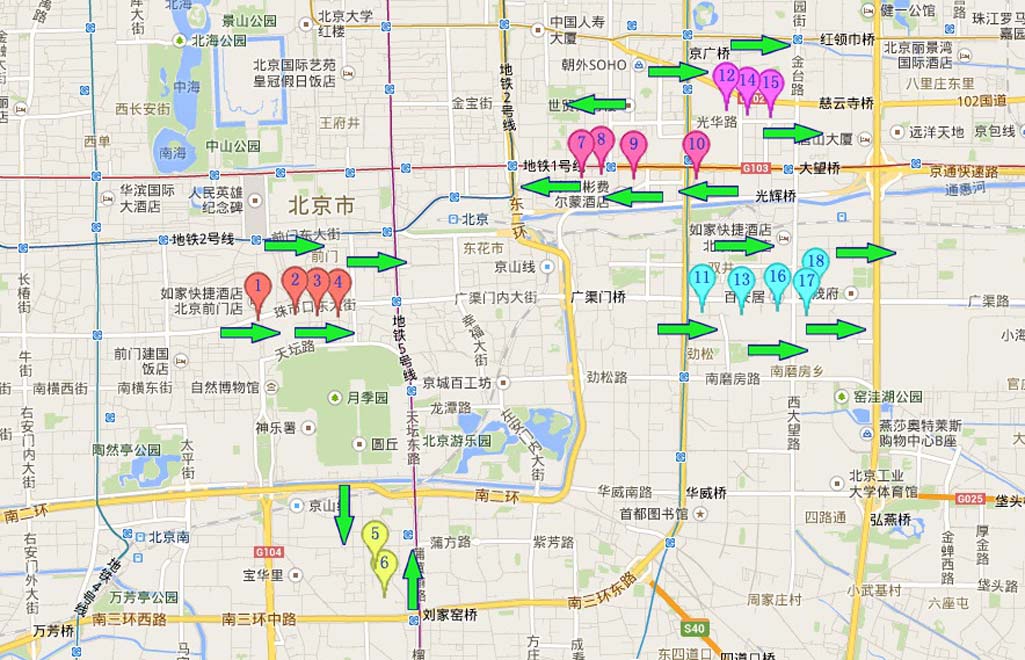
我们使用某些特定时间内的18个位置作为测试数据。每个位置都进行了测试从5到35次进行评估，共有425条测试数据。每个位置的平均测试次数约为23次。测试时间分布在2013年9月9日至2013年9月15日之间。每个测试位置仅在一个方向上进行测试。每个测试位置的方向从以下四个方向中选择其一：从东到西、从西到东、从北到南或从南到北。图5显示了这些位置的分布情况。

图6（从 a1到 d6）展示了 R和 cof不同参数下的不同结果。为了使概率更加明显，放大泊松分布的期望（λ） 是一个好方法。这可以保持概率之间的差异，并提供更好的用户体验。然后，我们定义参数 cof来表示 λ的放大倍数。

在这些图表中，x‐轴表示纬度，y‐轴表示经度，z‐轴表示分钟从当天00:00起经过的时间。每个圆圈代表一个样本数据，圆圈的位置表示该样本的地理位置、时间以及真实位置（圆圈在平面 z= 0上的投影；符号为+）。圆圈的颜色从红色到黄色变化，表示样本数据中打到出租车的概率。颜色越接近黄色，概率越高。圆圈的大小表示样本的等待时间，圆圈越大，等待时间越长。可以明显看出，较大的圆圈颜色更偏黄色；这有效证明了概率与等待时间之间存在反比关系。

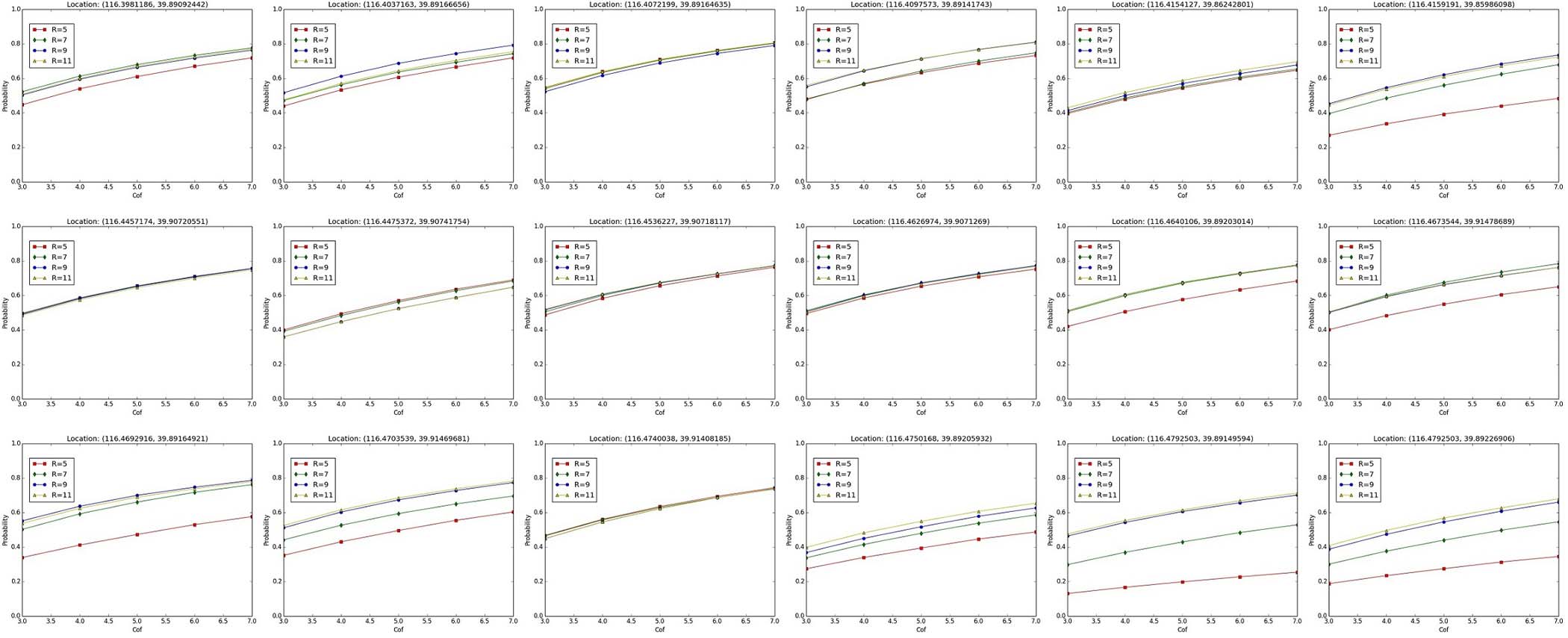
图7（从 a1到 c6）显示了在特定位置参数 R和 cof变化时的概率分布。在图7中，参数 R和 cof任一增加都会使概率上升。可以解释为 R是搜索范围的半径。当搜索范围扩大时，将包含更多的热点区域用于计算概率，且值概率会更高（由于样本数据并非在同一时间选取，某些图表可能显示 R较高但概率较低）。类似地，参数 cof是泊松分布中 λ的系数；概率与 cof成正比。有一个有趣的现象：如果某些位置具有相似的概率分布，则它们在现实中应当彼此靠近，且交通状况也相似。

在图8中，我们将我们的算法与朴素算法进行了比较。在朴素算法中，我们通过一个月内打到出租车的平均等待时间来计算等待时间，并通过一个月内打到空驶出租车的平均概率来计算PGTR。

IX. 结论

我们的贡献如下。根据出租车GPS历史数据，本文提出了一种在大数据环境下的出租车寻客数据处理系统，即出租车推荐系统（Taxi‐RS）。Taxi‐RS包含两个阶段：离线处理和快速在线处理。第一阶段包括离线数据预处理和离线图模型构建器。首先，我们计算了GPS数据中影像数据之间的特征值，并根据特征值的差异程度将大数据文件划分为七个部分。然后，我们在压缩数据上扫描热点以识别偏好轨迹。根据这些偏好轨迹，我们可以构建离线轨迹图模型。在进行在线查询时，可根据查询输入时间和位置，利用概率模型在轨迹图中快速搜索并计算查询结果。最后，输出查询结果。

进一步扩展当前工作有几个方面需要考虑。在现实生活中，城市出租车系统是一个随着时间推移而逐渐变化的动态系统。此外，该系统并非封闭，会受到外部因素（如道路施工、交通管制等）的显著影响。因此，仅凭一个月的GPS数据不足以支持持续的输出。经过较长时间后，旧的GPS数据将无法匹配实时出租车系统；因此，有必要根据最新的GPS数据及时更新模型。针对这一问题，我们提出以下建议。

1) 我们可以检查数据集的时间有效性，并剔除已过过期日期的无效数据。因此，我们需要用最新数据来覆盖离线模型。这种方法相对简单，但可能会舍弃一些仍有价值的旧数据，从而导致一定的误差。

2) 在此基础上，我们可以更渐进地替换旧数据。例如，我们可以通过 data in the model= the latest data× 0.8+the old data×0 对旧数据进行迭代更新。其优点是在丢弃时仍能保留旧数据的参考价值。

然而，如果我们使用上述两种方法，每次更新离线模型时都会花费很长时间。我们可以通过使用动态图或动态规划算法来优化更新时间，从而能够构建离线模型以更新新数据。