Laplace Equation
Contents[hide] |
Laplace Equation[edit]
The Laplace equation is a basic PDE that arises in the heat and diffusion equations. The Laplace equation is defined as:

Solution to Case with 1 Non-homogeneous Boundary Condition[edit]
In a condensed notation in (x,y,z) rectangular coordinates, the Laplace equation in two dimensions reduces to:
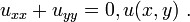
The solution to the case with 1 non-homogeneous boundary condition is the most basic solution type. For the purposes of this example, we consider that the following boundary conditions hold true for this equation:
Step 1: Separate Variables[edit]
To solve this equation, we assume that the function  is comprised of two functions
is comprised of two functions  and
and 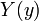 such that
such that 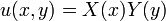 . Hence,
. Hence,  and
and  Making the substitutions into the Laplace equation, we get:
Making the substitutions into the Laplace equation, we get:

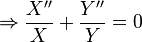
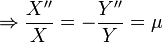
The 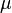 is called a separation constant because the solution to the equation must yield a constant. Because of the separation constant, it yields two linear ODEs:
is called a separation constant because the solution to the equation must yield a constant. Because of the separation constant, it yields two linear ODEs:
Step 2: Translate Boundary Conditions[edit]
Translating the boundary conditions allows us to divide the boundary conditions among the variables. This division yields:
Step 3: Solve the Sturm-Liouville Problem[edit]
The last two boundary conditions are homogeneous boundary conditions for the function  . Using the solution to the Sturm-Liouville problems (SLP), we can easily get a function for
. Using the solution to the Sturm-Liouville problems (SLP), we can easily get a function for  . The following is a fairly simple SLP:
. The following is a fairly simple SLP:

The solution to the SLP yields the following information:
The solution we obtained is a family of solutions dependent on the value for n.
Step 4: Solve Remaining ODE[edit]
The remaining ODE that we have doesn't have a SLP solution to it because we only know one boundary condition for it. We have to use what we obtained from the SLP solution to help us solve this ODE. We obtained the following information from steps 1 and 2:

From analyzing the second order ODE, we obtain the characteristic equation  Out of the solution set that results from the exponentials, the only viable solution that arises is:
Out of the solution set that results from the exponentials, the only viable solution that arises is:
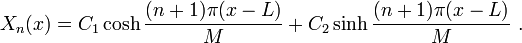
The substitution of (x-L) instead of x in the equation results only in a shift in the eigenspace, so it is valid and it helps us apply the boundary condition. Since 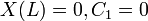 . For convenience, we choose
. For convenience, we choose  The resulting equation is:
The resulting equation is:

Step 5: Combine Solutions[edit]
We obtained equations for our separate variable functions and now we can substitute into our assumption in step 1. The substitution yields:

This function only satisfies the 3 homogeneous boundary conditions, however. To solve for the solution to the non-homogeneous boundary condition, we must consider that the complete solution consists of the following infinite series of terms:

At the non-homogeneous boundary condition:

This is an orthogonal expansion of 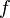 relative to the orthogonal basis of the sine function. The term
relative to the orthogonal basis of the sine function. The term  is a Fourier coefficient which is defined as the inner product:
is a Fourier coefficient which is defined as the inner product:

Thus, the coefficient of the infinite series solution 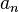 is:
is:
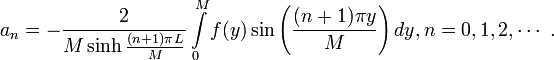
So, the entire general solution to the Laplace equation is:
![u(x,y)=\sum_{n=0}^\infty \left [ -\frac{2}{M\sinh\frac{(n+1)\pi L}{M}}\int\limits_{0}^{M} f(y)\sin\left(\frac{(n+1)\pi y}{M}\right) dy \right ] \sinh \frac{(n+1)\pi(x-L)}{M} \sin \frac{(n+1)\pi y}{M}~.](http://upload.wikimedia.org/wikiversity/en/math/f/b/4/fb481abb20992abd2b30b767ec368fce.png)
This is the general solution for the specific set of boundary conditions we assumed at the beginning. Other boundary conditions will yield a different solution. You can see the solution graphically by entering in a partial sum (e.g. n starts at 0 and ends at 10) into a numerical solver like Mathematica or Maple.
Solution to Case with 4 Non-homogeneous Boundary Conditions[edit]
Because  is a linear operator, any solutions to the equation
is a linear operator, any solutions to the equation  can be added together and the result will also be a solution to the equation. This is the superposition principle.
can be added together and the result will also be a solution to the equation. This is the superposition principle.
Because of superposition, we can solve the case where all four boundary conditions are non-homogeneous. To illustrate how this will work, let's take the boundary conditions:
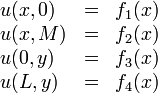
We divide this problem into 4 sub-problems, each one containing one of the non-homogeneous boundary conditions and each one subject to the Laplace equation condition,  We get the following boundary conditions for the 4 sub-problems:
We get the following boundary conditions for the 4 sub-problems:
In this case, we used all Dirichlet type boundary conditions, meaning that the boundary condition depends on the function value (e.g.  ). If you are using any combination of Dirichlet, Neumann (e.g.
). If you are using any combination of Dirichlet, Neumann (e.g.  ), Robin (e.g.
), Robin (e.g. 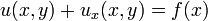 ) types of boundary conditions, the types of the boundary conditions should be preserved in every sub-problem (e.g. if
) types of boundary conditions, the types of the boundary conditions should be preserved in every sub-problem (e.g. if  , then the boundary condition is
, then the boundary condition is  when the boundary condition is made homogeneous and
when the boundary condition is made homogeneous and  when it is the non-homogeneous boundary condition in a sub-problem).
when it is the non-homogeneous boundary condition in a sub-problem).
Using the superposition principle, the complete solution to the 4 non-homogeneous boundary condition case is constructed by adding up all the solutions from the 4 sub-problems. In equation form, 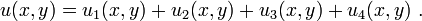 Each sub-problem can be solved using the method for the case with 1 non-homogeneous boundary condition as shown above.
Each sub-problem can be solved using the method for the case with 1 non-homogeneous boundary condition as shown above.








 本文详细介绍了拉普拉斯方程的基本概念及其在不同边界条件下的求解方法,包括单一非齐次边界条件和四个非齐次边界条件的情况,并通过分离变量法等步骤给出具体解的形式。
本文详细介绍了拉普拉斯方程的基本概念及其在不同边界条件下的求解方法,包括单一非齐次边界条件和四个非齐次边界条件的情况,并通过分离变量法等步骤给出具体解的形式。
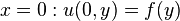
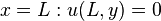






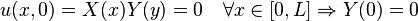
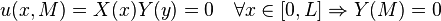
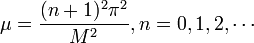

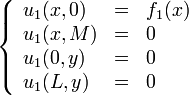



















 1268
1268

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








