七天学完十大机器学习经典算法-08.K均值聚类：无监督学习的万能分箱术-优快云博客

接上一篇《七天学完十大机器学习经典算法-07.朴素贝叶斯：概率思维的智慧》

想象你是一家超市的经理，面对堆积如山的顾客数据：年龄、消费频率、平均客单价...如何从中发现规律？你需要一种能自动将相似顾客分组的技术——这就是K均值聚类的魔力！作为无监督学习的代表算法，它能在没有预设标签的情况下，揭示数据的内在结构。

一、初识K均值：数据世界的自动分箱术

K均值聚类（K-Means Clustering） 是机器学习中最经典、应用最广泛的无监督学习算法之一。它的核心任务很简单：将给定的数据集划分为K个互斥的簇（Cluster），使得同一簇内的数据点尽可能相似，不同簇间的数据点尽可能不同。

核心概念解析

聚类 vs 分类：
- 分类：监督学习，已知类别标签（如"猫"/"狗"），预测新样本类别
- 聚类：无监督学习，没有预设标签，算法自行发现数据分组模式
- 类比：分类是按标签整理图书馆书籍；聚类是按内容相似性自动归类未贴标签的书
K值：预设的簇数量，是算法最关键的超参数
- 如将顾客分为3类（K=3）：高价值、中价值、低价值客户
质心（Centroid）：每个簇的"中心点"，是该簇所有点的平均位置
- 质心不一定是真实存在的数据点
距离度量：通常使用欧氏距离（直线距离）计算数据点间的相似度
- 公式：distance(A, B) = √(Σ(Ai - Bi)²)

# K均值伪代码
def k_means(data, K, max_iters=100):
    # 1. 随机初始化质心
    centroids = random_select(data, K)
    
    for _ in range(max_iters):
        clusters = [[] for _ in range(K)]
        
        # 2. 分配点到最近质心
        for point in data:
            distances = [distance(point, centroid) for centroid in centroids]
            cluster_idx = argmin(distances)
            clusters[cluster_idx].append(point)
        
        old_centroids = centroids.copy()
        
        # 3. 重新计算质心
        for i in range(K):
            if clusters[i]:  # 避免空簇
                centroids[i] = mean(clusters[i])
        
        # 4. 检查收敛
        if distance(old_centroids, centroids) < threshold:
            break
    
    return clusters, centroids

三、关键挑战与解决方案

挑战1：如何确定最佳K值？

肘部法则（Elbow Method）

计算不同K值对应的惯性（Inertia）：各点到其质心距离的平方和
公式：$J = \sum_{i=1}^{n} \min_{\mu_j \in C} ||x_i - \mu_j||^2$
绘制K-Inertia曲线，选择"肘点"（惯性下降变缓的转折点）

# 肘部法则Python实现
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

inertias = []
k_values = range(1, 10)

for k in k_values:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(data)
    inertias.append(kmeans.inertia_)

plt.plot(k_values, inertias, 'bo-')
plt.xlabel('K值')
plt.ylabel('惯性(Inertia)')
plt.title('肘部法则选择最佳K值')
plt.axvline(x=3, color='r', linestyle='--')  # 假设肘点在K=3
plt.show()

轮廓系数（Silhouette Score）

衡量簇内紧密度和簇间分离度的综合指标
取值范围[-1,1]，值越大表示聚类效果越好
公式：$s(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))}$
- $a(i)$：点i与同簇其他点的平均距离
- $b(i)$：点i到最近其他簇所有点的平均距离

# 轮廓系数评估
from sklearn.metrics import silhouette_score

best_k = 0
best_score = -1

for k in range(2, 10):
    kmeans = KMeans(n_clusters=k, random_state=42)
    labels = kmeans.fit_predict(data)
    score = silhouette_score(data, labels)
    
    if score > best_score:
        best_score = score
        best_k = k

print(f"最佳K值: {best_k}, 轮廓系数: {best_score:.4f}")

挑战2：随机初始化的不稳定性

K均值++算法

优化质心初始化过程：
1. 随机选择第一个质心
2. 计算所有点到最近质心的距离$D(x)$
3. 按概率$P(x) \propto D(x)^2$选择下一个质心
4. 重复直到选出K个质心
显著减少迭代次数，提高结果稳定性

# 使用K均值++初始化
kmeans = KMeans(n_clusters=3, init='k-means++', random_state=42)

挑战3：处理不同尺度特征

特征标准化

K均值基于距离度量，不同量纲特征会扭曲聚类结果
解决方案：使用StandardScaler或MinMaxScaler标准化特征

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)
kmeans.fit(data_scaled)

四、实战应用：从理论到实践

案例1：顾客细分（市场营销）

场景：某电商平台有10,000名顾客的年度消费数据：

年消费频率
平均客单价
最近购买时间（周数）

目标：将顾客分为3类制定精准营销策略

import pandas as pd
import seaborn as sns
from sklearn.cluster import KMeans

# 加载数据
customers = pd.read_csv('customer_data.csv')

# 特征选择
X = customers[['frequency', 'avg_spent', 'recency']]

# 特征标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# K均值聚类
kmeans = KMeans(n_clusters=3, init='k-means++', n_init=10, random_state=42)
customers['segment'] = kmeans.fit_predict(X_scaled)

# 分析聚类结果
segment_profile = customers.groupby('segment').agg({
    'frequency': 'mean',
    'avg_spent': 'mean',
    'recency': 'mean',
    'customer_id': 'count'
}).rename(columns={'customer_id': 'count'})

print(segment_profile)

# 可视化
sns.pairplot(customers, hue='segment', palette='viridis')
plt.suptitle('顾客分群可视化', y=1.02)
plt.show()

聚类解读：

高价值客户（红色）：高频次、高客单、近期活跃 → 专属VIP服务
流失风险客户（绿色）：低频次、低客单、久未购买 → 激活促销
潜力客户（蓝色）：中等消费，近期活跃 → 交叉销售推荐

案例2：图像压缩（计算机视觉）

原理：将图片中所有像素点的RGB值聚类，用K种颜色替代原始图像的颜色

from sklearn.utils import shuffle
import numpy as np
from PIL import Image

# 加载图像
image = Image.open('landscape.jpg')
image = np.array(image) / 255.0  # 归一化

# 获取像素数据
h, w, d = image.shape
pixels = image.reshape(-1, 3)  # 转换为N×3矩阵

# 随机采样加速计算
sample_size = 1000
pixel_sample = shuffle(pixels, random_state=42)[:sample_size]

# 寻找最佳K值（颜色数）
inertias = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(pixel_sample)
    inertias.append(kmeans.inertia_)

# 根据肘部法则选择K=8
k = 8

# 全像素聚类
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(pixels)

# 重建压缩图像
compressed_pixels = kmeans.cluster_centers_[kmeans.labels_]
compressed_image = compressed_pixels.reshape(h, w, d)

# 保存结果
Image.fromarray((compressed_image * 255).astype(np.uint8)).save('compressed.jpg')

print(f"原始图像存储: {h*w*24} bits")
print(f"压缩后存储: {h*w*np.log2(k) + k*24} bits")  # 存储标签+颜色表

效果对比：

原始图像：1600万色 → 3.8MB
K=8压缩：8种颜色 → 0.2MB（压缩率95%）
应用场景：网页优化、医学图像存储、卫星图像传输

案例3：文档主题聚类（自然语言处理）

场景：对10,000篇新闻文章自动分组

from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# 加载文本数据
documents = load_news_corpus()  # 假设返回文本列表

# 文本向量化
vectorizer = TfidfVectorizer(max_features=2000, stop_words='english')
X = vectorizer.fit_transform(documents)

# 降维可视化
pca = PCA(n_components=2)
X_2d = pca.fit_transform(X.toarray())

# 聚类（假设K=6）
kmeans = KMeans(n_clusters=6, random_state=42)
clusters = kmeans.fit_predict(X)

# 可视化聚类结果
plt.figure(figsize=(10, 8))
scatter = plt.scatter(X_2d[:, 0], X_2d[:, 1], c=clusters, cmap='viridis', alpha=0.6)
plt.title('新闻文档聚类可视化')
plt.xlabel('PCA 1')
plt.ylabel('PCA 2')
plt.colorbar(scatter, label='Cluster')
plt.show()

# 查看每个簇的主题词
feature_names = vectorizer.get_feature_names_out()
order_centroids = kmeans.cluster_centers_.argsort()[:, ::-1]

for i in range(6):
    print(f"\nCluster #{i} 主题词:")
    for ind in order_centroids[i, :10]:
        print(f" {feature_names[ind]}", end='')

五、K均值的优缺点与适用场景

优点：

简单高效：算法直观，时间复杂度O(n×K×I×d)，适用于大数据
可扩展性强：有分布式实现（如Spark MLlib）
结果可解释：质心代表簇的"平均特征"
广泛适用：数值型数据均可应用

缺点：

需要预设K值：确定最佳K值需要额外技术
对初始质心敏感：不同初始化可能产生不同结果
对异常值敏感：离群点会显著影响质心位置
只适合凸形簇：难以处理复杂形状的簇（如环形）
需要特征缩放：未标准化的特征会扭曲距离计算

改进算法：

算法名称	解决的核心问题	适用场景
K-Medoids	对异常值敏感	噪声数据，分类特征
DBSCAN	非凸形状聚类	空间数据，异常检测
GMM	软聚类（概率分配）	重叠簇，密度估计
BIRCH	超大规模数据效率问题	流式数据，内存受限环境

六、最佳实践指南

数据预处理流程：

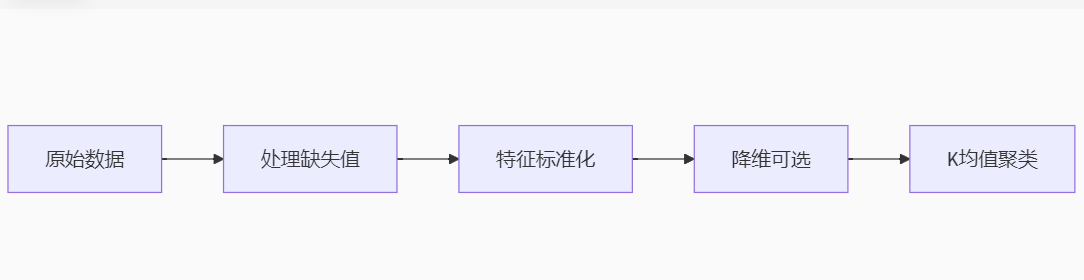
参数调优技巧：
- 始终使用n_init>1（推荐10-25次）减少随机性影响
- 结合肘部法则和轮廓系数确定K值
- 对文本数据先用TF-IDF向量化
- 对高维数据先用PCA降维
结果评估方法：
- 内部评估：轮廓系数、Davies-Bouldin指数
- 外部评估（如果有标签）：调整兰德指数(ARI)、标准化互信息(NMI)
- 业务验证：聚类结果是否具有实际意义
实用小贴士：
- 对时间序列数据，使用动态时间规整(DTW)替代欧氏距离
- 处理分类特征时，使用K-Prototypes算法
- 可视化时，优先选择t-SNE而非PCA（保留局部结构更好）