常数e

常数e

高等数学中的e全称为自然常数e。

1.e的由来

自然一词是指自然界的现象，是客观存在的或者说是本有的属性。比如自然数。ｅ是人们在利息的计算中发现的一个极限的数字，因为是本身就存在。只是被人类发现了，故称之为自然常数。

2.e的计算

（1）e的精确值是没办法计算出的，因为e是无理数，是一个无限不循环小数，因此我们只能计算出他的近似值。

（2）根据高等数学中的极限公式，可以求出：当n->∞时，

所以求e的近似值，可让n取100，1000，10000，100000等，然后利用计算机来计算。如：

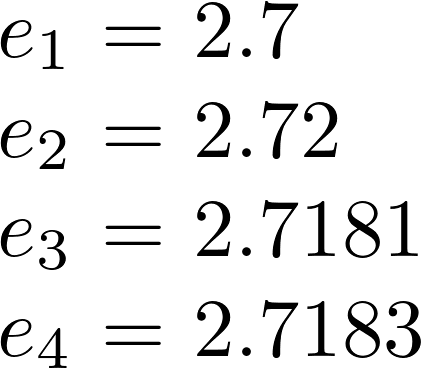
3.例子

假设本金为１元，年利率为100%，
如果一年发一次利息，即一共发一次利息，那么一年后账户余额为1+1=２元。
如果半年发一次利息，即一共发两次利息，发完利息你立刻将利息存入，一年后账户余额为１+ 1/2 + (1+1/2)/2=2.25元。
现在假设每年发ｎ次利息，则最后账户余额为：1+1/n+(1+1/n)/n+(1+1/n+(1+1/n)/n)/n+……………
如果ｎ趋于正无穷，那么最后的结果就是ｅ。

 

知识补充：

极限lim

极限是微积分中的基础概念，它指的是变量在一定的变化过程中，从总的来说逐渐稳定的这样一种变化趋势以及所趋向的值（极限值）。

在高等数学中，极限是一个重要的概念。

极限可分为数列极限和函数极限

1.数列极限

设 {Xn} 为实数列，a 为定数．若对任给的正数 ε，总存在正整数N，使得当 n>N 时有∣Xn-a∣<ε 则称数列{Xn} 收敛于a，定数 a 称为数列 {Xn} 的极限，Xn→a（n→∞）或

ε越小，表示接近得越近；而正数ε可以任意地变小，说明Xn与常数a可以接近到任何不断地靠近的程度。

2.函数极限

设函数 在点 的某一去心邻域内有定义，如果存在常数A，对于任意给定的正数  （无论它多么小），总存在正数 ，使得当x满足不等式  时，对应的函数值  都满足不等式：

|f(x)-A|<ε，则称函数f当x趋于+∞时以A为极限，记作

lim f(x) = A 或 f(x)->A(x->+∞)

转载于:https://www.cnblogs.com/oneself/p/11435234.html