关于Numpy矩阵乘法报错以及广播机制的说明

a = np.random.randn(4, 3) # a.shape = (4, 3)
b = np.random.randn(3, 2) # b.shape = (3, 2)
c = a * b

报错

经过查阅资料，发现Numpy中矩阵乘法需要使用.dot()或者.matmul()

import numpy as np
a = np.random.randn(4, 3) # a.shape = (4, 3)
b = np.random.randn(3, 2) # b.shape = (3, 2)
c = np.matmul(a,b)
#c=np.dot(a,b)
print(c)

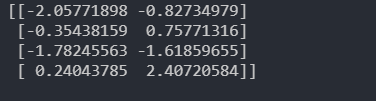
若是点乘的话需要维度一致才可以

import numpy as np
a = np.random.randn(4, 3) 
b = np.random.randn(4, 3)
c = a*b
print(c)

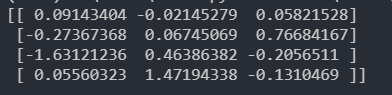
此外Numpy还有广播机制

import numpy as np
a = np.random.randn(3, 3)
b = np.random.randn(3, 1)
c = a * b
print(c)

虽然a,b的维度不一致，但是由于b后缘维度是1，可以广播，广播沿轴长度为1 的轴进行，即b的列向量会复制3次
计算结果如下