Batch Normalization
对一个batch内的数据计算均值和方差,将数据归一化为均值为0、方差为1的正态分布数据,最后用对数据进行缩放和偏移来还原数据本身的分布:

BN测试和训练时的差异
核心区别在于统计量(均值和方差)的来源与计算方式,训练时计算Batch内数据的均值 (μbatchμ_{batch}μbatch) 和方差 (σbatch2σ²_{batch}σbatch2),测试时使用全局训练数据的滑动平均计算均值和方差。
目的:保证输出的确定性、一致性和处理任意大小输入的能力。
以下是主要差异的详细对比:
| 特征 | 训练阶段 (Training) | 测试阶段 (Inference/Evaluation) |
|---|---|---|
| 统计量来源 | 当前 Mini-Batch 的样本 | 固定的全局统计量 (训练阶段估计的) |
| 均值 (μ) 计算 | μbatch=1m∑i=1mxi\mu_{\text{batch}} = \frac{1}{m} \sum_{i=1}^{m} x_iμbatch=m1∑i=1mxi | 使用训练阶段估计的 E[x]E[x]E[x] (滑动平均) |
| 方差 (σ²) 计算 | σbatch2=1m∑i=1m(xi−μbatch)2\sigma^2_{\text{batch}} = \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu_{\text{batch}})^2σbatch2=m1∑i=1m(xi−μbatch)2 | 使用训练阶段估计的 Var[x]\text{Var}[x]Var[x] (滑动平均) |
| 归一化公式 | x^i=xi−μbatchσbatch2+ε\hat{x}_i = \frac{x_i - \mu_{\text{batch}}}{\sqrt{\sigma^2_{\text{batch}} + \varepsilon}}x^i=σbatch2+εxi−μbatch | x^i=xi−E[x]Var[x]+ε\hat{x}_i = \frac{x_i - E[x]}{\sqrt{\text{Var}[x] + \varepsilon}}x^i=Var[x]+εxi−E[x] |
| 可学习参数 (γ, β) | 更新 (通过反向传播) | 固定 (使用训练好的值) |
| 目的 | 1. 加速收敛 2. 缓解内部协变量偏移 3. 提供正则化效果 | 提供稳定的、确定性的输出 |
| 依赖 Batch Size | 是 (统计量依赖当前Batch) | 否 (使用固定统计量,单样本也可运行) |
| 随机性 | 有 (不同Batch统计量不同) | 无 (输出是确定的) |
-
训练阶段:
- 动态统计量: 对于每个输入 Mini-Batch,BN层计算 该Batch内数据 的均值 (μbatchμ_{batch}μbatch) 和方差 (σbatch2σ²_{batch}σbatch2)。
- 归一化: 使用μbatchμ_{batch}μbatch 和 σbatch2σ²_{batch}σbatch2对 Batch 内的每个样本进行归一化:μbatch=1m∗∑i=1mxiμ_{batch} = \frac{1}{m} * \sum_{i=1}^{m}x_iμbatch=m1∗∑i=1mxi(其中
ε是一个很小的数,防止除以零)。 - 缩放与偏移: 应用可学习的缩放因子
γ和偏移因子 β:yi=γ∗x^i+ββ:y_i = γ * x̂_i + ββ:yi=γ∗x^i+β。这赋予了网络在必要时恢复原始表示的能力。 - 更新全局统计量: 训练过程中会持续估计整个训练数据集的均值和方差的指数移动平均 (Exponential Moving Average - EMA) 或简单平均:
- E[x]=momentum∗E[x]+(1−momentum)∗μbatchE[x] = momentum * E[x] + (1 - momentum) * μ_{batch}E[x]=momentum∗E[x]+(1−momentum)∗μbatch
- Var[x]=momentum∗Var[x]+(1−momentum)∗σbatch2Var[x] = momentum * Var[x] + (1 - momentum) * σ²_{batch}Var[x]=momentum∗Var[x]+(1−momentum)∗σbatch2
- 这里的 momentummomentummomentum 通常接近 1,例如 0.9, 0.99,表示更依赖历史估计值)。这个
E[x]和Var[x]就是最终用于测试阶段的固定统计量。
-
测试阶段:
- 固定统计量: 不再使用当前输入数据计算均值和方差 而是使用在整个训练过程结束后确定下来的固定值
E[x]和Var[x](即训练阶段通过EMA计算得到的全局估计值)。 - 归一化: 使用固定的
E[x]和Var[x]对每个测试样本进行归一化: x^i=(xi−E[x])Var[x]+εx̂_i =\frac{(x_i - E[x])}{\sqrt{Var[x] + ε}}x^i=Var[x]+ε(xi−E[x])。 - 缩放与偏移: 使用训练好的、固定的参数
γ和β: yi=γ∗x^i+βy_i = γ * x̂_i + βyi=γ∗x^i+β。 - 目的: 确保网络在处理单个样本或任意大小的 Batch (甚至 Batch Size=1) 时,其行为是确定性的和一致的。输出不依赖于测试时其他样本的统计量。
- 固定统计量: 不再使用当前输入数据计算均值和方差 而是使用在整个训练过程结束后确定下来的固定值
为什么测试阶段不能使用 Batch 统计量?
- 一致性要求: 训练好的模型在部署时,对于相同的输入,应该总是产生相同的输出。如果在测试时使用当前 Batch 的统计量,那么:
- 同一个样本在不同 Batch 中(例如和不同的其他样本组合在一起)会得到不同的归一化结果,导致模型输出不同。这是不可接受的。
- 无法处理 Batch Size=1 的情况(因为无法计算有意义的均值和方差)。
- 全局最优估计: 训练阶段积累的
E[x]和Var[x]是对整个训练数据集统计特性的最优估计,比单个测试 Batch 的统计量更能代表数据的真实分布。使用它们能得到更稳定、更泛化的结果。
在代码中如何体现?
现代深度学习框架 (PyTorch, TensorFlow/Keras) 通过 train() 和 eval() 模式自动处理这种差异:
model.train(): 将模型置于训练模式。BN 层使用当前 Batch 的统计量计算μ_batch和σ²_batch,并更新其内部的running_mean(E[x]) 和running_var(Var[x])。model.eval(): 将模型置于评估/测试模式。BN 层停止更新running_mean和running_var,并直接使用它们存储的固定值E[x]和Var[x]进行归一化计算。
# PyTorch 示例
model.train() # 训练模式
# 进行训练迭代... BN层会更新running_mean/running_var
model.eval() # 评估/测试模式
with torch.no_grad(): # 通常同时禁用梯度计算
# 进行测试或推理... BN层使用固定的running_mean/running_var
Batch Norm 1d
用于 2D 输入(如全连接层的输出或时序数据),输入形状为b*c, 即在特征维度c上进行归一化:
import torch
import torch.nn as nn
class MyBatchNorm1d:
def __init__(self, num_features, eps=1e-5, momentum=0.1, affine=True):
self.num_features = num_features
self.eps = eps
self.momentum = momentum
self.affine = affine
# 可学习参数
if self.affine:
self.gamma = torch.ones(num_features)
self.beta = torch.zeros(num_features)
else:
self.gamma = None
self.beta = None
# 运行时统计量
self.running_mean = torch.zeros(num_features)
self.running_var = torch.ones(num_features)
# 训练模式标志
self.training = True
def forward(self, x):
if self.training:
# 计算当前批次的均值和方差
batch_mean = x.mean(dim=0)
batch_var = x.var(dim=0, unbiased=False) # 使用有偏估计
# 更新全局统计量
self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * batch_mean
self.running_var = (1 - self.momentum) * self.running_var + self.momentum * batch_var
else:
# 推理时使用保存的统计量
batch_mean = self.running_mean
batch_var = self.running_var
# 归一化
x_hat = (x - batch_mean) / torch.sqrt(batch_var + self.eps)
# 缩放和偏移(如果启用)
if self.affine:
x_hat = self.gamma * x_hat + self.beta
return x_hat
# 测试代码
if __name__ == "__main__":
# 模拟输入 (batch_size=3, num_features=5)
x = torch.randn(3, 5)
bn_custom = MyBatchNorm1d(5, affine=True)
bn_custom.gamma = bn_native.weight.clone().detach()
bn_custom.beta = bn_native.bias.clone().detach()
bn_custom.running_mean = bn_native.running_mean.clone()
bn_custom.running_var = bn_native.running_var.clone()
output_custom = bn_custom.forward(x)
Batch Norm 2d
用于 4D 输入(如卷积层的输出)输入形状为b*c*h*w,即在每个通道上进行normalization,求b*h*w内的像素求均值和方差。
class MyBatchNorm2d:
def __init__(self, num_features, eps=1e-5, momentum=0.1, affine=True):
self.num_features = num_features
self.eps = eps
self.momentum = momentum
self.affine = affine
# 可学习参数
if self.affine:
self.gamma = torch.ones(num_features)
self.beta = torch.zeros(num_features)
else:
self.gamma = None
self.beta = None
# 运行时统计量
self.running_mean = torch.zeros(num_features)
self.running_var = torch.ones(num_features)
# 训练模式标志
self.training = True
def forward(self, x):
# 输入形状: (B, C, H, W)
if self.training:
# 计算当前批次的均值和方差(沿 B, H, W 维度)
batch_mean = x.mean(dim=(0, 2, 3)) # 形状变为 [C]
batch_var = x.var(dim=(0, 2, 3), unbiased=False) # 有偏估计
# 更新全局统计量
self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * batch_mean
self.running_var = (1 - self.momentum) * self.running_var + self.momentum * batch_var
else:
batch_mean = self.running_mean
batch_var = self.running_var
# 归一化(需要保持维度对齐)
x_hat = (x - batch_mean[None, :, None, None]) / torch.sqrt(batch_var[None, :, None, None] + self.eps)
# 缩放和偏移(如果启用)
if self.affine:
x_hat = self.gamma[None, :, None, None] * x_hat + self.beta[None, :, None, None]
return x_hat
# 测试代码
if __name__ == "__main__":
# 模拟输入 (batch_size=2, channels=3, height=4, width=4)
x = torch.randn(2, 3, 4, 4)
# 手动实现
bn_custom = MyBatchNorm2d(3, affine=True)
bn_custom.gamma = bn_native.weight.clone().detach()
bn_custom.beta = bn_native.bias.clone().detach()
bn_custom.running_mean = bn_native.running_mean.clone()
bn_custom.running_var = bn_native.running_var.clone()
output_custom = bn_custom.forward(x)
作用
a、防止过拟合
b、加速网络的收敛,internal covariate shift导致上层网络需要不断适应底层网络带来的分布变化
c、缓解梯度爆炸和梯度消失
局限 依赖于batch size,适用于batch size较大的情况
Layer normalization
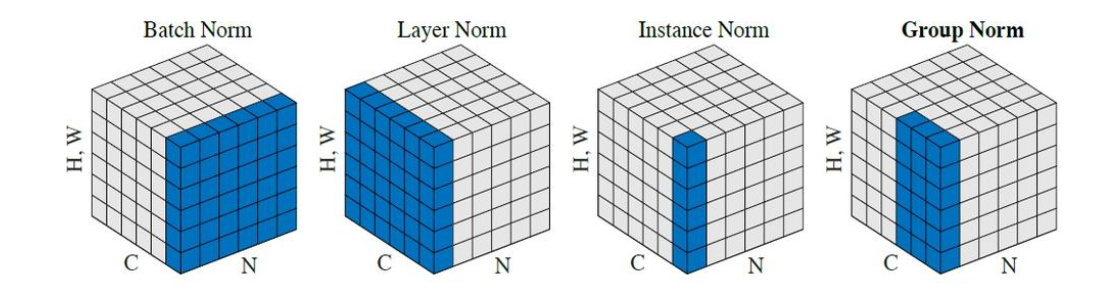
与Batch Normalization不同,Layer Normalization在每个样本上独立进行,而不是在每个批次上进行。对每个样本的所有特征进行归一化,如N*C*H*W,对每个C*H*W进行归一化,得到N个均值和方差。
对于一个给定的输入张量 XXX(假设是二维的,即 X∈Rn×dX \in \mathbb{R}^{n \times d}X∈Rn×d),其中 nnn 是样本数量,ddd 是特征维度(即C*H*W),Layer Normalization的步骤如下:
-
计算均值:对于每个样本 xix_ixi(其中 xi∈Rdx_i \in \mathbb{R}^dxi∈Rd),计算其均值 μi\mu_iμi:
μi=1d∑j=1dxij \mu_i = \frac{1}{d} \sum_{j=1}^d x_{ij} μi=d1j=1∑dxij -
计算方差:对于每个样本 xix_ixi,计算其方差 σi2\sigma_i^2σi2:
σi2=1d∑j=1d(xij−μi)2 \sigma_i^2 = \frac{1}{d} \sum_{j=1}^d (x_{ij} - \mu_i)^2 σi2=d1j=1∑d(xij−μi)2 -
归一化:对于每个样本 xix_ixi,使用其均值和方差进行归一化:
x^ij=xij−μiσi2+ϵ \hat{x}_{ij} = \frac{x_{ij} - \mu_i}{\sqrt{\sigma_i^2 + \epsilon}} x^ij=σi2+ϵxij−μi
其中 ϵ\epsilonϵ 是一个很小的常数,用于避免除以零。 -
仿射变换:对于归一化后的样本 x^i\hat{x}_ix^i,使用可学习的参数 γ\gammaγ 和 β\betaβ 进行缩放和偏移:
yi=γx^i+β y_i = \gamma \hat{x}_i + \beta yi=γx^i+β
其中 γ\gammaγ 和 β\betaβ 是 ddd维向量。
代码实现:
import torch
import torch.nn as nn
class LayerNorm(nn.Module):
def __init__(self, features, eps=1e-5):
super().__init__()
self.gamma = nn.Parameter(torch.ones(features)) # 缩放参数
self.beta = nn.Parameter(torch.zeros(features)) # 平移参数
self.eps = eps # 数值稳定项
def forward(self, x):
# 在最后一个维度计算均值和方差
mean = x.mean(dim=-1, keepdim=True)
var = x.var(dim=-1, keepdim=True, unbiased=False)
# 归一化
x_normalized = (x - mean) / torch.sqrt(var + self.eps)
# 仿射变换
return self.gamma * x_normalized + self.beta
Instance normalization
Instance normalization对每个样本的每个通道特征进行归一化,输入张量维度为(N,C,H,W)(N, C, H, W)(N,C,H,W):NNN:批大小,CCC:通道数,HHH:高度,WWW:宽度。Instance normalization对每个H*W进行归一化,得到N*C个均值和方差。
均值与方差计算
对每个样本nnn和通道ccc单独计算: μnc=1HW∑h=1H∑w=1Wxnchw \mu_{nc} = \frac{1}{HW}\sum_{h=1}^{H}\sum_{w=1}^{W}x_{nchw} μnc=HW1h=1∑Hw=1∑Wxnchw σnc2=1HW∑h=1H∑w=1W(xnchw−μnc)2 \sigma_{nc}^2 = \frac{1}{HW}\sum_{h=1}^{H}\sum_{w=1}^{W}(x_{nchw}-\mu_{nc})^2 σnc2=HW1h=1∑Hw=1∑W(xnchw−μnc)2
归一化
x^nchw=xnchw−μncσnc2+ϵ \hat{x}_{nchw} = \frac{x_{nchw} - \mu_{nc}}{\sqrt{\sigma_{nc}^2 + \epsilon}} x^nchw=σnc2+ϵxnchw−μnc
仿射变换
ynchw=γcx^nchw+βc y_{nchw} = \gamma_c \hat{x}_{nchw} + \beta_c ynchw=γcx^nchw+βc 其中γc\gamma_cγc和βc\beta_cβc为可学习参数,ϵ\epsilonϵ为极小常数防止除零
import torch
import torch.nn as nn
class InstanceNorm(nn.Module):
def __init__(self, num_features, eps=1e-5):
super().__init__()
self.eps = eps
self.gamma = nn.Parameter(torch.ones(1, num_features, 1, 1))
self.beta = nn.Parameter(torch.zeros(1, num_features, 1, 1))
def forward(self, x):
# 输入x形状: (N, C, H, W)
mean = torch.mean(x, dim=[2,3], keepdim=True) # 计算均值
var = torch.var(x, dim=[2,3], keepdim=True, unbiased=False) # 计算方差
# 归一化
x_normalized = (x - mean) / torch.sqrt(var + self.eps)
# 缩放平移
return self.gamma * x_normalized + self.beta
Group normalization
输入特征张量:设输入特征张量为X∈RN×C×H×WX \in \mathbb{R}^{N \times C \times H \times W}X∈RN×C×H×W,其中:NNN: 批量大小;CCC: 通道数;H,WH,WH,W: 空间维度
分组处理:每个样本按通道分组进行归一化,将通道分为GGG组,每组含C/GC/GC/G个通道,定义组索引g∈[1,...,G]g \in [1,...,G]g∈[1,...,G],则每个组的特征张量为Xn,g∈R1×(C/G)×H×WX_{n,g} \in \mathbb{R}^{1 \times (C/G) \times H \times W}Xn,g∈R1×(C/G)×H×W
μng=1(C/G)HW∑c=(g−1)(C/G)g(C/G)−1∑h=1H∑w=1WXnchw \mu_{ng} = \frac{1}{(C/G)HW} \sum_{c=(g-1)(C/G)}^{g(C/G)-1} \sum_{h=1}^{H} \sum_{w=1}^{W} X_{nchw} μng=(C/G)HW1c=(g−1)(C/G)∑g(C/G)−1h=1∑Hw=1∑WXnchw
σng2=1(C/G)HW∑c=(g−1)(C/G)g(C/G)−1∑h=1H∑w=1W(Xnchw−μng)2 \sigma_{ng}^2 = \frac{1}{(C/G)HW} \sum_{c=(g-1)(C/G)}^{g(C/G)-1} \sum_{h=1}^{H} \sum_{w=1}^{W} (X_{nchw} - \mu_{ng})^2 σng2=(C/G)HW1c=(g−1)(C/G)∑g(C/G)−1h=1∑Hw=1∑W(Xnchw−μng)2
标准化处理
对原始值进行标准化:
X^nchw=Xnchw−μngσng2+ϵ \hat{X}{nchw} = \frac{X{nchw} - \mu_{ng}}{\sqrt{\sigma_{ng}^2 + \epsilon}} X^nchw=σng2+ϵXnchw−μng
仿射变换
加入可学习参数γc\gamma_cγc和βc\beta_cβc:
Ynchw=γcX^nchw+βc Y_{nchw} = \gamma_c \hat{X}_{nchw} + \beta_c Ynchw=γcX^nchw+βc






















 705
705

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








