#LeetCode——39.数组总和

难度：medium

一、题目介绍

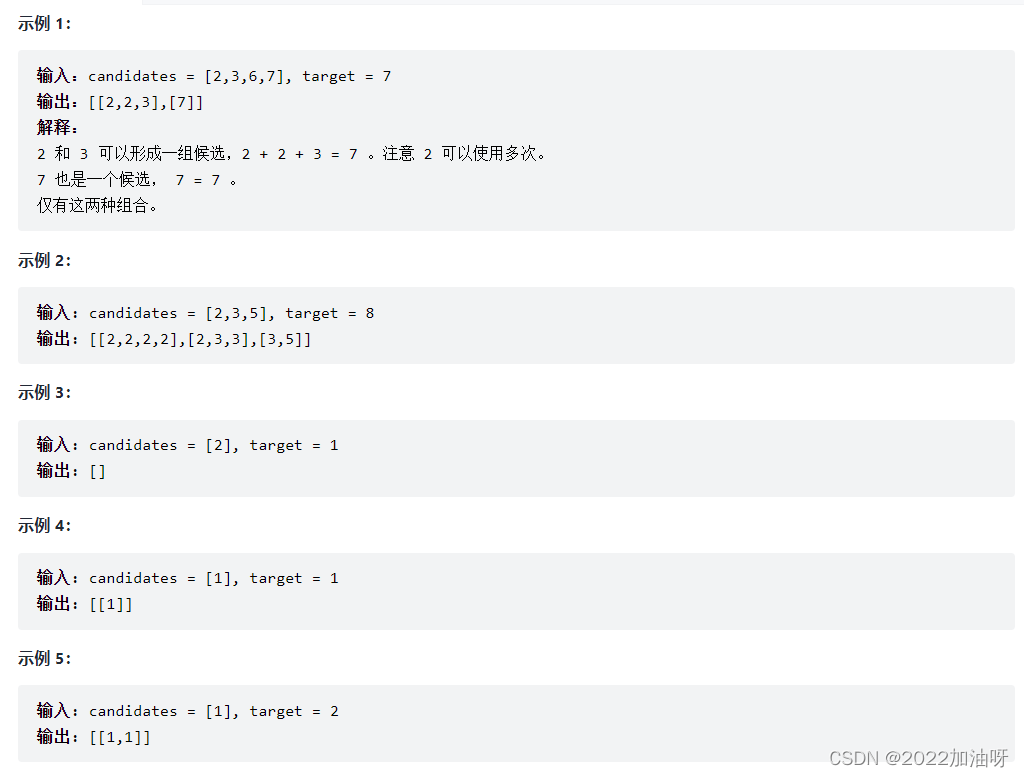
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。 

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

 

二、思路分析 

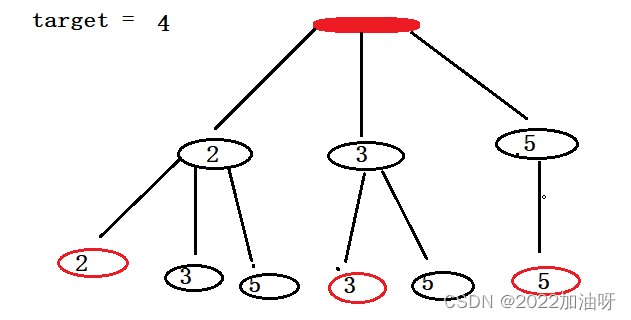
 这道题与组合的区别就是：需要多一个变量来保存每个结点的和，在进行回溯操作时，不仅将 com【保存每种解法】删除操作，还要将 target 减去相应结点的值。

回溯算法的要素：

参数及返回值：返回值一般都是void 。参数有 candidates[] , int target ,List com【保存每种解法】，int sum【保存结点的和】，int start【每次递归开始搜索的位置】

终止条件：1、当 sum == target 时，将com加入结果集result中  2、当sum > target时，没必要在进行递归了，直接return

收集结果：将结点增加到 com 中，并且要更新  sum 的值。

递归操作：递归时需注意一点，题目中表示每种解法中可以有重复的元素。所以递归的出发结点都是从自身开始

回溯操作：不仅要将 com 集合中的元素删除一个，还要将 target 减去删除元素的值

代码：

public class LeetCode_39_backtrack {
    //保存最终结果集
    List<List<Integer>> result = new ArrayList<>();

    public static void main(String[] args) {
        int[] candidates = {2, 3, 5};
        int target = 8;

        LeetCode_39_backtrack l = new LeetCode_39_backtrack();
        List<List<Integer>> result = l.combinationSum(candidates, target);
        System.out.println(result);
    }

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<Integer> com = new ArrayList<>();
        backtrack(candidates, com, target,0,0);
        return result;
    }

    private void backtrack(int[] candidates, List<Integer> com, int target, int sum, int start) {
        /*
            俩个终止条件：
            
                当sum大于target，就没有必要再去递归了
                当sum等于target,说明符合条件，有一种解
         */
        if (sum > target) {
            return;
        }
        if (sum == target) {
            result.add(new ArrayList<>(com));
        }
        for (int i = start; i < candidates.length; i++) {
            com.add(candidates[i]);
            //求和
            sum += candidates[i];
            //由于每种解法中允许有重复的元素。
            backtrack(candidates,com,target,sum,i);
            //回溯操作
            sum -= candidates[i];
            com.remove(com.size()-1);
        }
    }
}