2023合肥市信息学科普日小学组市赛题解_[2023合肥市小学组] 存钱(saving)-优快云博客

1.存钱（saving）

[问题描述]

了解到山区贫困学生的生活状况后，小可可决定从下周一开始每天都从自己的零用钱

中节省一部分存起来，等存到一定数额后，捐给贫困山区的学生。假设小可可周一到周五

每天能节省 a 元，周六和周日每天节省 b 元，那么他将在第几天实现存款数额超过或正

好等于 c 元呢？

[输入格式]

输入数据共 1 行由空格分隔的 3 个正整数，分别表示 a 、b 和 c。

[输出格式]

共 1 行一个正整数，表示满足条件的天数。

[样例输入输出]

样例输入 10 15 85

样例输出 8

#include<bits/stdc++.h>
using namespace std;
int n,s1,s2,s3;
int main()
{
	int a,b,c,s=0,tian=0;
	cin>>a>>b>>c;
	while(s<c)
	{
		if(tian%7>=1&&tian%7<=5)
		{
			s=s+a;
		}
		else
		{
			s=s+b;
		}
		tian++;
	} 
	cout<<tian;
	return 0;
}

样例解释： 5 * 10 + 15 + 15 + 10 = 90 > 85,第 8 天能存到 90 元。

[数据范围]

1≤a 、b 、c≤10 15

2. 逆波兰式计算（rpn）

[问题描述]

逆波兰表达式又叫做后缀表达式，是波兰逻辑学家 J.卢卡西维兹于 1929 年首先提出的一

种表达式的表示方法，它把运算数写在前面，把运算符写在后面，逆波兰式中只有运算符和

运算数。如 a + b 的逆波兰式为 ab+ ，a + b - c 的逆波兰式为 ab+c- ，a+（ b – c）

的逆波兰式为 abc-+ 。现在小可可有一个已知的逆波兰式，请帮他计算这个逆波兰式的

值吧。一种计算逆波兰式值的方法是从左向右扫描逆波兰式，遇到运算符就计算，为简化

计算，假设这个逆波兰式中只有+ 、- 两种运算符。

[输入格式]

共 2 行。第一行 1 一个正整数 n，表示逆波兰式中数值的个数（包括运算符和运算数），

第二行为逆波兰式，其中每个数值 p 由空格分隔。保证每个逆波兰式都是正确可计算的。

[输出格式]

共 1 行 1 个整数，表示逆波兰式的值。

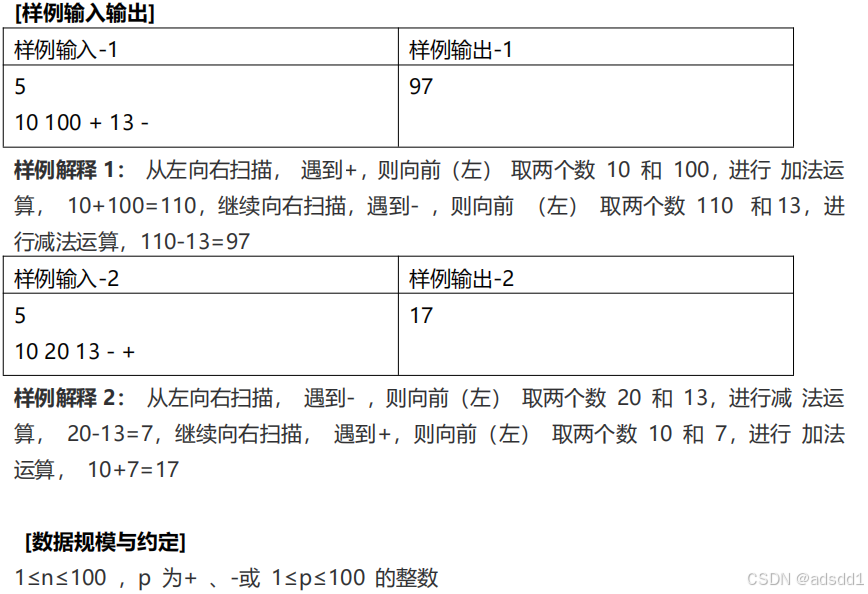
题解：这题就是典型的模拟算法题，在此之前需要大家看看关于C++STL模板库中栈的运用，还有就是逆波兰公式的用法。

#include<bits/stdc++.h>
using namespace std;
stack<int> st;//定义栈
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		string s;
		cin>>s;
		if(s=="+"||s=="-")//判断输入的是否是符号
		{
			if(s=="+")
			{
				int a=st.top();//保存第一个栈顶元素
				st.pop();//弹出栈顶元素
				int b=st.top();//保存第二个栈顶元素
				st.pop();
				st.push(a+b);
			}
			else
			{
				int a=st.top();
				st.pop();
				int b=st.top();
				st.pop();
				st.push(b-a);
			}	
		}
		else
		{
			st.push(atoi(s.c_str()));//把字符转变成数字然后压入栈
		}
	}
	cout<<st.top();//输出栈顶元素，也就是最终结果
	return 0;
}

3. 自动驾驶（autopilot）

[问题描述]

作为人工智能的重要应用领域，自动驾驶有望重塑现有的交通模式。小可可团队正在

研发一种自动驾驶算法模型，模型约定汽车在单位时间内行驶状态只有下列四种：

前进，用大写字母“F”表示。

后退，用大写字母“B”表示。

左转，用大写字母“L”表示。

右转，用大写字母“R”表示。

算法运行一段时间后，汽车的行驶过程可以描述为一条长度为 n，且仅包含大写字

母“F”、“B”、“L”和“R”的字符串 S。小可可关注的是 S 串中由 k 个连续字符

组成的子串，其中有些子串在 S 串中反复出现。现在，小可可请你统计出所有重复出

现的长度为 k 的子串数量，这对预测汽车行驶状态的研究有重要意义。

[输入格式]

共 2 行，第一行输入 2 个正整数 n, k，分别表示字符串 S 的长度和子串的长度。

第二行：长度为 n，由大写字母“F”、“B”、“L”和“R”组成的字符串 S。

[输出格式]

共 1 行一个整数，表示表示字符串 S 中出现次数大于 1 的长度为 k 的子串数量。

题解：这题也是模拟算法，需要对字符串进行截取，枚举从第i个字符串开始每次截取k个，然后映射到map容器中进行计数，这里需要大家去看看关于STL模板库map容器的知识。

#include<bits/stdc++.h>
using namespace std;
map<string,int>mp;//定义map容器
int n,k,cnt;
string s;
int main()
{
	string s;
	cin>>n>>k>>s;
	for(int i=0;i<n-k+1;i++)
	{
		string s1=s.substr(i,k);//从第i个元素开始截取k个字符
		mp[s1]++;//截取到的字符映射到map容器并且将对应的value值加一
		if(mp[s1]>=2)//比较是否超过或者等于2
		{
			cnt++;
		}
	}
	cout<<cnt;
	return 0;
}

4. K 阶恒星系（kgalaxy）

[问题描述]

半人马座 A 是个巨大的椭圆星系，具有 n 个恒星。和太阳系一样，每个恒星周围都有许多行星。小可可团队通过太空望远镜，观测出每个恒星系里行星的数量，其中第 i 个恒星系里有 pi（1 ≤ i ≤ n）个行星。若第 i 个恒星系为小可可定义的 K 阶恒星系，则在正整数序列 p1,p2, … pn 中， pi 的左边和右边都至少有 k 个元素的值小于 pi （如图 1 所示）。（这个图有些错误，前面的p1,p1,p1应该是p1,p2,p3）

现在，小可可请你统计出半人马座 A 中 K 阶恒星系的数量。

[输入格式]

输入数据有 2 行，第一行输入 2 个正整数 n, k，分别表示恒星的数量和满足定义的

k 值。第二行：由 n 个正整数构成的序列 p1,p2,… pn。

[输出格式]

一行一个正整数，表示半人马座 A 中 K 阶恒星系的数量。

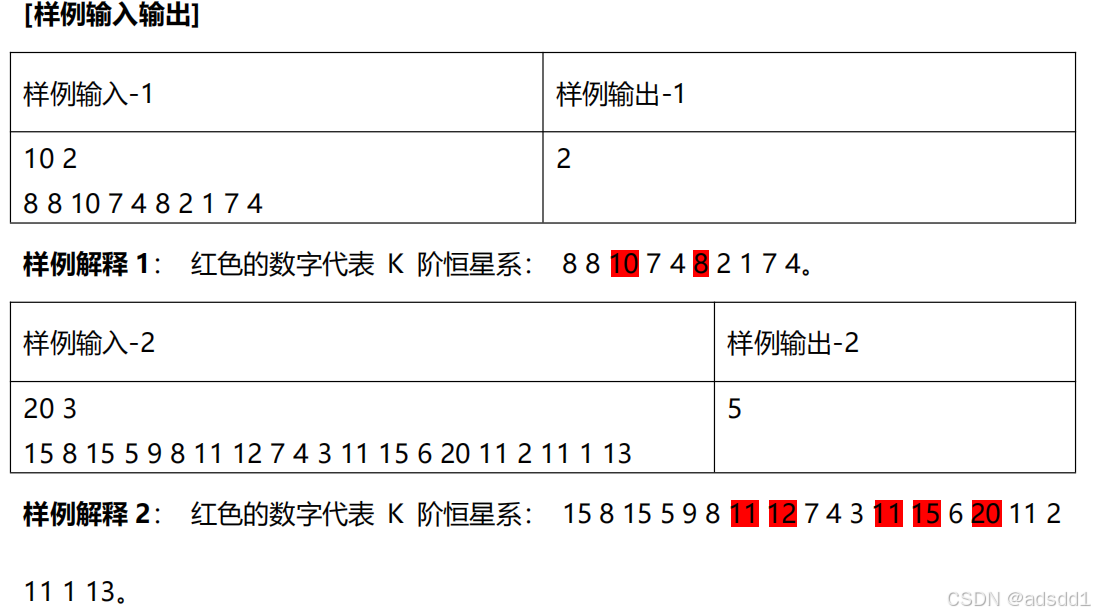
题解：这题有两种解法，第一种直接枚举，把每个i左边和右边的数据都搜索一遍这种写法肯定超时大概能拿个10-20分，第二种解法需要用树状数组大家可以先去看一下树状数组有关知识然后再看代码。（树状数组稍微有点难，如果有不理解的同学可以私信我讲解）

枚举法：

#include<bits/stdc++.h>
using namespace std;
const int N=1000005;
int a[N],n,k,cnt;
int main()
{
	cin>>n>>k;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	for(int i=1;i<=n;i++)
	{
		int zuo=0,you=0;
		for(int j=1;j<=i-1;j++)
		{
			if(a[i]>a[j])
			{
				zuo++;
			}
		}
		for(int j=i+1;j<=n;j++)
		{
			if(a[i]>a[j])
			{
				you++;
			}
		}
		if(zuo>=k&&you>=k)
		{
			cnt++;
		}
	}
	cout<<cnt;
	return 0;
}

树状数组法：

#include<bits/stdc++.h>
using namespace std;
const int N=1000005;
int a[N],n,p,k;//a是原数组
int c[N],l[N],r[N],cnt=0;//c是树状数组用来记录阶段小于a[i]的和
void updata(int x)//树状数组点更新
{
	for(int i=x;i<=n;i+=i&(-i))
	{
		c[i]++;
	}
}
int qiuhe(int x)//求前缀和
{
	int s=0;
	for(int i=1;i<=x;i+=i&(-i))
	{
		s=s+c[i];
	}
	return s;
}
int main()
{
	cin>>n>>k;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	for(int i=1;i<=n;i++)
	{
		updata(a[i]);
		l[i]=qiuhe(a[i]-1);//求第i个恒星的左边有几个小于a[i]的元素个数
	}
	memset(c,0,sizeof(c));
	for(int i=n;i>=1;i--)//求第i个恒星的右边有几个小于a[i]的元素个数
	{
		updata(a[i]);
		r[i]=qiuhe(a[i]-1);
		if(l[i]>k&&r[i]>k)
		{
			cnt++;
		}
	}
	cout<<cnt;
	return 0;
}