行为型模式:③解释器模式(Interpreter Pattern)
核心思想
定义一种语言的文法规则,并构建一个解释器来解释该语言中的句子。核心是将复杂的语法拆解为 “终结符表达式”(不可再分的基本单位,如数字)和 “非终结符表达式”(由多个表达式组合而成,如加减运算),通过组合这些简单表达式形成抽象语法树(AST),最终由解释器递归遍历语法树,执行解释逻辑。
核心本质
语法拆解 + 递归解释,将复杂问题(如表达式计算、简单脚本解析)分解为可重复的简单子问题,通过组合子问题的解得到最终结果。
典型场景
简单数学表达式计算(如 3+5-2、a*b+c);
配置文件解析(如简单的键值对语法、规则配置);
自定义小型脚本语言(如游戏中的简单指令、规则引擎);
正则表达式解析(正则本身就是一种文法,正则引擎是解释器)。
C语言编写
场景示例
简单数学表达式解释(仅支持整数加减运算):
文法规则:表达式 → 数字 | 表达式 + 数字 | 表达式 - 数字;
角色划分:
1.抽象表达式(AbstractExpression):定义解释接口;
2.终结符表达式(TerminalExpression):数字表达式(不可再分);
3.非终结符表达式(NonterminalExpression):加法表达式、减法表达式(由两个子表达式组合);
4.上下文(Context):存储待解释的表达式字符串、解析位置、中间结果;
5.客户端:构建语法树,触发解释。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h>
// -------------------------- 1. 上下文(Context):存储解释所需状态 --------------------------
typedef struct Context {
char expr[64]; // 待解释的表达式字符串
int pos; // 当前解析位置(指针)
int result; // 解释结果
} Context;
// 初始化上下文
void context_init(Context* ctx, const char* expr) {
strncpy(ctx->expr, expr, sizeof(ctx->expr)-1);
ctx->pos = 0;
ctx->result = 0;
}
// 跳过空格(辅助解析)
void skip_whitespace(Context* ctx) {
while (ctx->expr[ctx->pos] != '\0' && isspace(ctx->expr[ctx->pos])) {
ctx->pos++;
}
}
// 解析数字(从当前位置提取整数,更新pos)
int parse_number(Context* ctx) {
skip_whitespace(ctx);
int num = 0;
while (ctx->expr[ctx->pos] != '\0' && isdigit(ctx->expr[ctx->pos])) {
num = num * 10 + (ctx->expr[ctx->pos] - '0');
ctx->pos++;
}
skip_whitespace(ctx);
return num;
}
// -------------------------- 2. 抽象表达式(AbstractExpression):解释接口 --------------------------
typedef struct Expression {
// 解释方法:接收上下文,返回解释结果
int (*interpret)(struct Expression* self, Context* ctx);
// 销毁表达式
void (*destroy)(struct Expression* self);
} Expression;
// -------------------------- 3. 终结符表达式(TerminalExpression):数字表达式 --------------------------
typedef struct NumberExpression {
Expression base;
int number; // 存储数字值(终结符,不可再分)
} NumberExpression;
// 数字表达式的解释:直接返回数字值
int number_interpret(Expression* self, Context* ctx) {
NumberExpression* num_expr = (NumberExpression*)self;
return num_expr->number;
}
// 销毁数字表达式
void number_destroy(Expression* self) {
free(self);
}
// 创建数字表达式(客户端或解析器调用)
Expression* create_number_expression(int number) {
NumberExpression* num_expr = (NumberExpression*)malloc(sizeof(NumberExpression));
num_expr->base.interpret = number_interpret;
num_expr->base.destroy = number_destroy;
num_expr->number = number;
return (Expression*)num_expr;
}
// -------------------------- 4. 非终结符表达式(NonterminalExpression):加减运算表达式 --------------------------
// 加法表达式(左表达式 + 右表达式)
typedef struct AddExpression {
Expression base;
Expression* left; // 左子表达式(可是数字或其他非终结符)
Expression* right; // 右子表达式
} AddExpression;
// 加法表达式的解释:递归解释左右子表达式,结果相加
int add_interpret(Expression* self, Context* ctx) {
AddExpression* add_expr = (AddExpression*)self;
int left_val = add_expr->left->interpret(add_expr->left, ctx);
int right_val = add_expr->right->interpret(add_expr->right, ctx);
return left_val + right_val;
}
// 销毁加法表达式(递归销毁子表达式)
void add_destroy(Expression* self) {
AddExpression* add_expr = (AddExpression*)self;
if (add_expr->left != NULL) {
add_expr->left->destroy(add_expr->left);
}
if (add_expr->right != NULL) {
add_expr->right->destroy(add_expr->right);
}
free(self);
}
// 创建加法表达式
Expression* create_add_expression(Expression* left, Expression* right) {
AddExpression* add_expr = (AddExpression*)malloc(sizeof(AddExpression));
add_expr->base.interpret = add_interpret;
add_expr->base.destroy = add_destroy;
add_expr->left = left;
add_expr->right = right;
return (Expression*)add_expr;
}
// 减法表达式(左表达式 - 右表达式)
typedef struct SubExpression {
Expression base;
Expression* left;
Expression* right;
} SubExpression;
// 减法表达式的解释:递归解释左右子表达式,结果相减
int sub_interpret(Expression* self, Context* ctx) {
SubExpression* sub_expr = (SubExpression*)self;
int left_val = sub_expr->left->interpret(sub_expr->left, ctx);
int right_val = sub_expr->right->interpret(sub_expr->right, ctx);
return left_val - right_val;
}
// 销毁减法表达式(递归销毁子表达式)
void sub_destroy(Expression* self) {
SubExpression* sub_expr = (SubExpression*)self;
if (sub_expr->left != NULL) {
sub_expr->left->destroy(sub_expr->left);
}
if (sub_expr->right != NULL) {
sub_expr->right->destroy(sub_expr->right);
}
free(self);
}
// 创建减法表达式
Expression* create_sub_expression(Expression* left, Expression* right) {
SubExpression* sub_expr = (SubExpression*)malloc(sizeof(SubExpression));
sub_expr->base.interpret = sub_interpret;
sub_expr->base.destroy = sub_destroy;
sub_expr->left = left;
sub_expr->right = right;
return (Expression*)sub_expr;
}
// -------------------------- 5. 解析器(Parser):构建抽象语法树(AST) --------------------------
// 递归解析表达式(根据文法规则构建语法树)
// 文法:expr → number | expr '+' number | expr '-' number
Expression* parse_expression(Context* ctx) {
// 第一步:解析第一个数字(终结符),作为左表达式的初始值
int num = parse_number(ctx);
Expression* left = create_number_expression(num);
// 循环解析后续的运算符和数字(非终结符组合)
while (ctx->expr[ctx->pos] != '\0') {
char op = ctx->expr[ctx->pos];
if (op != '+' && op != '-') {
break; // 非加减运算符,解析结束
}
ctx->pos++; // 跳过运算符
// 解析运算符后的数字(右表达式)
int right_num = parse_number(ctx);
Expression* right = create_number_expression(right_num);
// 根据运算符创建对应的非终结符表达式,更新左表达式为新的组合表达式
if (op == '+') {
left = create_add_expression(left, right);
} else if (op == '-') {
left = create_sub_expression(left, right);
}
}
return left; // 返回构建好的语法树根节点
}
// -------------------------- 测试代码(客户端) --------------------------
int main() {
// 待解释的表达式(简单加减运算)
const char* expr1 = "3 + 5 - 2";
const char* expr2 = "10 - 3 + 4 - 1";
// 解析并解释第一个表达式
Context ctx1;
context_init(&ctx1, expr1);
Expression* ast1 = parse_expression(&ctx1);
int result1 = ast1->interpret(ast1, &ctx1);
printf("表达式:%s → 结果:%d\n", expr1, result1);
ast1->destroy(ast1);
// 解析并解释第二个表达式
Context ctx2;
context_init(&ctx2, expr2);
Expression* ast2 = parse_expression(&ctx2);
int result2 = ast2->interpret(ast2, &ctx2);
printf("表达式:%s → 结果:%d\n", expr2, result2);
ast2->destroy(ast2);
return 0;
}
实现关键要点
1.文法拆解核心:将复杂表达式(如 3+5-2)拆解为 “终结符”(数字 3、5、2)和 “非终结符”(+、- 运算),非终结符通过组合子表达式形成语法树。
2.抽象表达式接口:Expression 结构体用 interpret 函数指针定义统一解释接口,终结符和非终结符表达式都实现该接口,确保递归调用一致性。
3.递归解释逻辑:非终结符表达式(如 AddExpression)的 interpret 方法递归调用左、右子表达式的解释方法,将子结果组合为当前结果,符合 “分而治之” 思想。
4.上下文作用:Context 存储待解析的字符串、当前解析位置,避免解释过程中重复传递参数,同时可缓存中间结果(如示例中的 result 字段,可扩展用于复杂场景)。
5.解析器构建语法树:parse_expression 函数根据文法规则递归构建抽象语法树(AST),客户端无需关心语法树细节,仅需调用解析器和解释方法。
6.内存管理:非终结符表达式销毁时需递归销毁子表达式,避免内存泄漏(如 add_destroy 递归销毁 left 和 right 子表达式)。
7.扩展性限制:C 语言中新增运算符(如乘法 *)需新增 MulExpression 结构体和对应的 interpret/destroy 函数,修改解析器逻辑,符合开闭原则,但代码修改成本略高。
C++语言实现(类 + 继承 + 多态 + 递归)
通过 “抽象基类 + 子类继承” 定义表达式接口,利用多态实现递归解释,STL 简化字符串处理,智能指针自动管理内存,语法树构建更清晰。
场景示例
同 C 语言:简单数学表达式解释(加减运算),角色划分一致,用类和继承替代结构体 + 函数指针。
#include <iostream>
#include <string>
#include <memory> // 智能指针
#include <cctype>
// -------------------------- 1. 上下文(Context):存储解析和解释状态 --------------------------
class Context {
public:
explicit Context(std::string expr) : expr_(std::move(expr)), pos_(0) {}
// 跳过空格
void SkipWhitespace() {
while (pos_ < expr_.size() && std::isspace(expr_[pos_])) {
pos_++;
}
}
// 解析数字(更新pos_)
int ParseNumber() {
SkipWhitespace();
int num = 0;
while (pos_ < expr_.size() && std::isdigit(expr_[pos_])) {
num = num * 10 + (expr_[pos_] - '0');
pos_++;
}
SkipWhitespace();
return num;
}
// 获取当前位置的字符
char CurrentChar() const {
return pos_ < expr_.size() ? expr_[pos_] : '\0';
}
// 移动解析指针
void MoveNext() { pos_++; }
private:
std::string expr_; // 待解释的表达式
size_t pos_; // 当前解析位置
};
// -------------------------- 2. 抽象表达式(AbstractExpression):基类接口 --------------------------
class Expression {
public:
virtual ~Expression() = default; // 虚析构:确保子类析构被调用
// 纯虚函数:解释方法,返回计算结果
virtual int Interpret(Context& ctx) const = 0;
};
// -------------------------- 3. 终结符表达式(TerminalExpression):数字表达式 --------------------------
class NumberExpression : public Expression {
public:
explicit NumberExpression(int number) : number_(number) {}
int Interpret(Context& ctx) const override {
return number_; // 终结符直接返回自身值
}
private:
int number_;
};
// -------------------------- 4. 非终结符表达式(NonterminalExpression):加减运算表达式 --------------------------
// 加法表达式
class AddExpression : public Expression {
public:
AddExpression(std::shared_ptr<Expression> left, std::shared_ptr<Expression> right)
: left_(std::move(left)), right_(std::move(right)) {}
int Interpret(Context& ctx) const override {
// 递归解释左右子表达式,结果相加
return left_->Interpret(ctx) + right_->Interpret(ctx);
}
private:
std::shared_ptr<Expression> left_; // 左子表达式(智能指针自动管理内存)
std::shared_ptr<Expression> right_; // 右子表达式
};
// 减法表达式
class SubExpression : public Expression {
public:
SubExpression(std::shared_ptr<Expression> left, std::shared_ptr<Expression> right)
: left_(std::move(left)), right_(std::move(right)) {}
int Interpret(Context& ctx) const override {
// 递归解释左右子表达式,结果相减
return left_->Interpret(ctx) - right_->Interpret(ctx);
}
private:
std::shared_ptr<Expression> left_;
std::shared_ptr<Expression> right_;
};
// -------------------------- 5. 解析器(Parser):构建抽象语法树 --------------------------
class Parser {
public:
// 递归解析表达式,返回语法树根节点
std::shared_ptr<Expression> Parse(Context& ctx) {
// 解析第一个数字(终结符)
int num = ctx.ParseNumber();
std::shared_ptr<Expression> left = std::make_shared<NumberExpression>(num);
// 循环解析后续运算符和数字
while (ctx.CurrentChar() != '\0') {
char op = ctx.CurrentChar();
if (op != '+' && op != '-') {
break; // 非加减运算符,解析结束
}
ctx.MoveNext(); // 跳过运算符
// 解析右侧数字
int right_num = ctx.ParseNumber();
std::shared_ptr<Expression> right = std::make_shared<NumberExpression>(right_num);
// 构建非终结符表达式,更新左表达式
if (op == '+') {
left = std::make_shared<AddExpression>(left, right);
} else if (op == '-') {
left = std::make_shared<SubExpression>(left, right);
}
}
return left;
}
};
// -------------------------- 测试代码(客户端) --------------------------
int main() {
// 待解释的表达式
std::string expr1 = "3 + 5 - 2";
std::string expr2 = "10 - 3 + 4 - 1";
// 解析器
Parser parser;
// 解释第一个表达式
Context ctx1(expr1);
auto ast1 = parser.Parse(ctx1);
int result1 = ast1->Interpret(ctx1);
std::cout << "表达式:" << expr1 << " → 结果:" << result1 << std::endl;
// 解释第二个表达式
Context ctx2(expr2);
auto ast2 = parser.Parse(ctx2);
int result2 = ast2->Interpret(ctx2);
std::cout << "表达式:" << expr2 << " → 结果:" << result2 << std::endl;
return 0; // 智能指针自动销毁语法树,无需手动释放
}
实现关键要点
1.抽象基类定义接口:Expression 基类用纯虚函数 Interpret 定义统一解释接口,所有具体表达式(数字、加减)继承并实现该接口,多态确保递归调用的一致性。
2.智能指针管理内存:非终结符表达式用 std::shared_ptr 持有子表达式,自动管理内存,避免手动递归销毁,虚析构函数确保子类析构被正确调用。
3.上下文封装更完善:Context 类封装了解析所需的所有状态(表达式字符串、解析位置)和辅助方法(SkipWhitespace、ParseNumber),代码更整洁,复用性强。
4.解析器职责单一:Parser 类专注于构建抽象语法树(AST),客户端仅需创建上下文、调用解析器和解释方法,无需关心语法树的构建细节。
5.扩展性更强:新增运算符(如乘法 *)时,仅需新增 MulExpression 类继承 Expression,实现 Interpret 方法,修改解析器的运算符判断逻辑,完全符合开闭原则。
6.类型安全:C++ 的编译期类型检查和多态机制,避免 C 语言中函数指针绑定错误或类型转换风险,代码更可靠。
7.递归逻辑清晰:非终结符表达式的 Interpret 方法通过多态调用子表达式的 Interpret,递归层次分明,符合文法的递归定义。
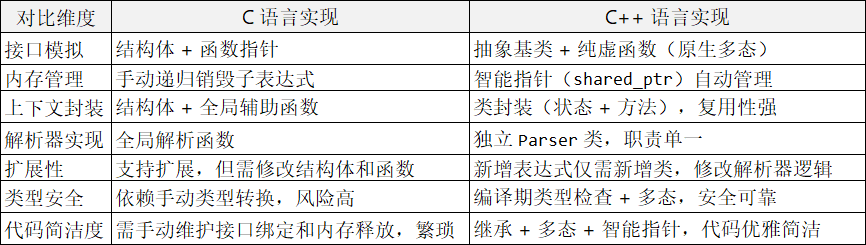
解释器模式核心总结(C vs C++)
设计原则
开闭原则:新增文法规则(如运算符)时,仅需新增表达式类,无需修改现有代码;
单一职责原则:每个表达式仅负责自身的解释逻辑,解析器负责构建语法树,上下文负责存储状态;
组合原则:非终结符表达式通过组合子表达式形成复杂结构,本质是组合模式的应用。





















 566
566

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








