本文深入探讨了链表这一数据结构的原理与特性，包括单向链表与双向链表的区别，链表的存储结构，以及创建、插入、删除、输出等基本操作的实现。通过代码示例，详细解释了链表的插入、删除操作，并分析了链表的性能特点，如查找、插入和删除的时间复杂度。此外，还讨论了链表在实际应用中的优势和局限，以及如何在特定场景下高效使用链表。
链表
什么是链表
链表与数据结构有些不同。栈和队列都是申请一段连续的空间，然后按顺序存储数据；链表是一种物理上非连续、非顺序的存储结构，数据元素之间的顺序是通过每个元素的指针关联的。
链表由一系列节点组成，每个节点一般至少会包含两部分信息：一部分是元素数据本身，另一部分是指向下一个元素地址的指针。这样的存储结构让链表相比其他线性的数据结构来说，操作会复杂一些。
与数组相比，链表具有其优势：链表克服了数组需要提前设置长度的缺点，在运行时可以根据需要随意添加元素；计算机的存储空间并不总是连续可用的，而链表可以灵活地使用存储空间，还能更好地对计算机的内存进行动态管理。
链表分为两种类型：单向链表和双向链表。我们平时说道的链表指的是单向链表。双向链表的每个节点除存储元素数据本身为，还额外存储两个指针，分别指向上一个节点和下一个节点的地址。
当然，除了这些普通的链表，链表由于其特点还衍生了很多特殊的情况。
链表的存储结构
对于链表来说，我们只需要关心链表之间的关系，不需要关心链表实际存储的位置，以在表示一个链表关系时，一般使用箭头来关联两个连续的元素节点。
链表的存储结构如图2-13所示。
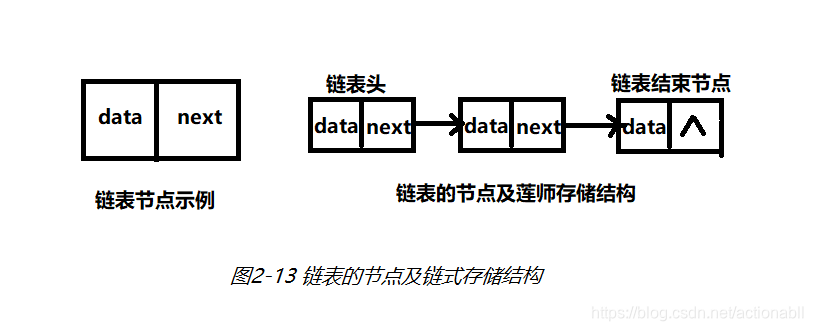
从链表的存储结构可知，链表的每个节点包含两个部分，分别是数据（叫做data）和指向下个节点地址的指针（叫做next）。在存储了一个链表之后怎么找到它？这里需要一个头结点，这个头结点是一个链表的第1个节点，它的指针指向下一个节点的地址，以此类推，直到指针指向为空时，便表示没有下一个元素了。
链表的操作
链表的操作有：创建、插入、删除、输出。
这里提到的插入、删除操作，其位置并不一定是开头或者结尾。由于链表特殊的存储结构，在链表中间进行数据元素的插入与删除也是很容易实现的。
创建操作就是空间的分配，把头、尾指针及链表节点数等信息初始化，这里就不详细介绍了。
在看实现代码之前，我们先通过存储结构看看链表的插入、删除是如何操作的。
1.插入操作
插入操作分为三种情况，分别是头插入、尾插入、中间插入。
头插入的操作，实际上是增加一个新的节点，然后把新增加的节点的指针指向原来头指针指向的元素，再把头指针指向新增的节点，如图2-14所示（途中的虚线表示被移除的指向）。
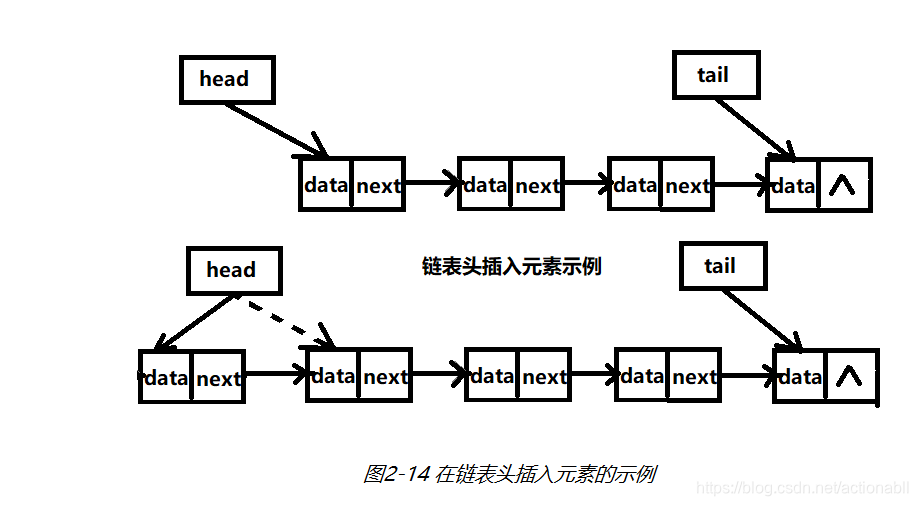
尾插入的操作，也是增加一个指针为空的节点，然后把原尾指针指向节点的指针指向新增加的节点，最后把尾指针指向新增加的节点即可，如图2-15所示。
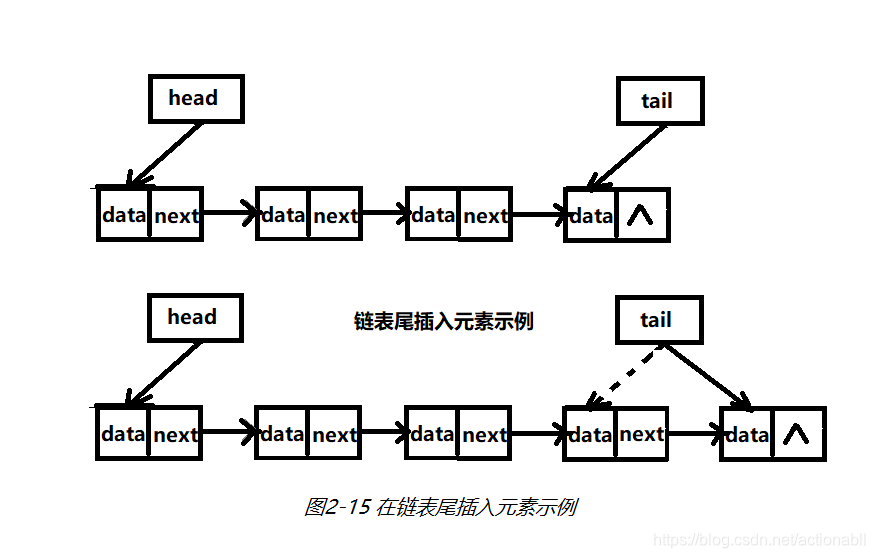
中间插入元素的操作会稍微复杂一些。首先怎加一个节点，然后把新增加的节点的指针指向插入位置的后一个位置的节点，把插入位置的前一个节点的指针指向新增加的节点即可，如图2-16所示。
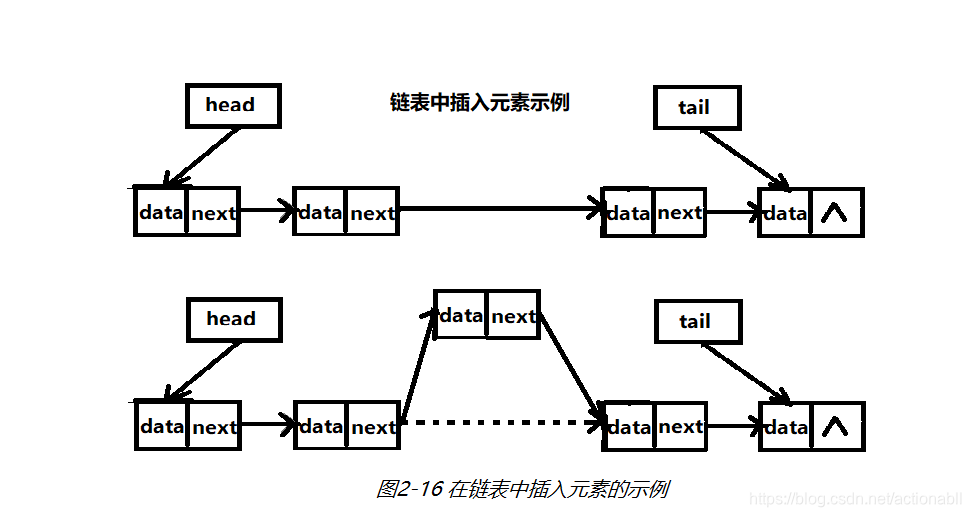
2.删除操作
删除头元素时，先把头指针指向下一个节点，然后把原头结点的指针置空，示意如图2-17所示。
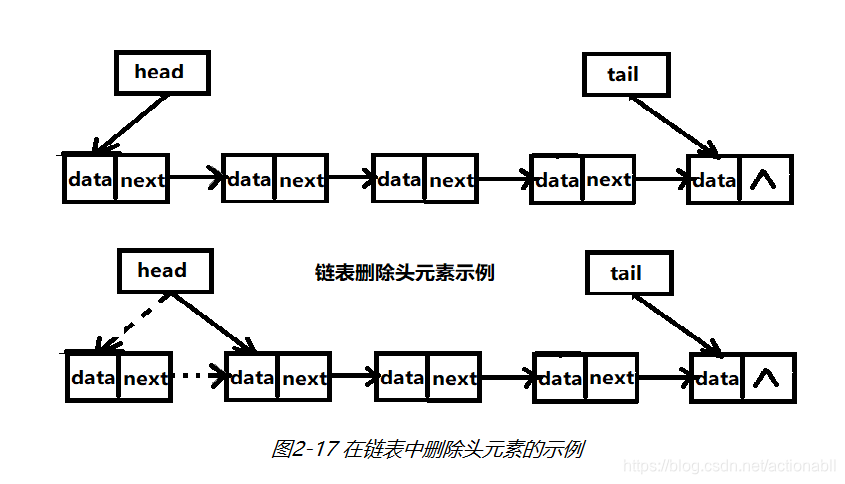
删除尾元素时，首先找到链表中倒数第2个元素，然后把尾指针指向这个元素，接着把原倒数第2个元素的尾指针置空，如图2-18所示。
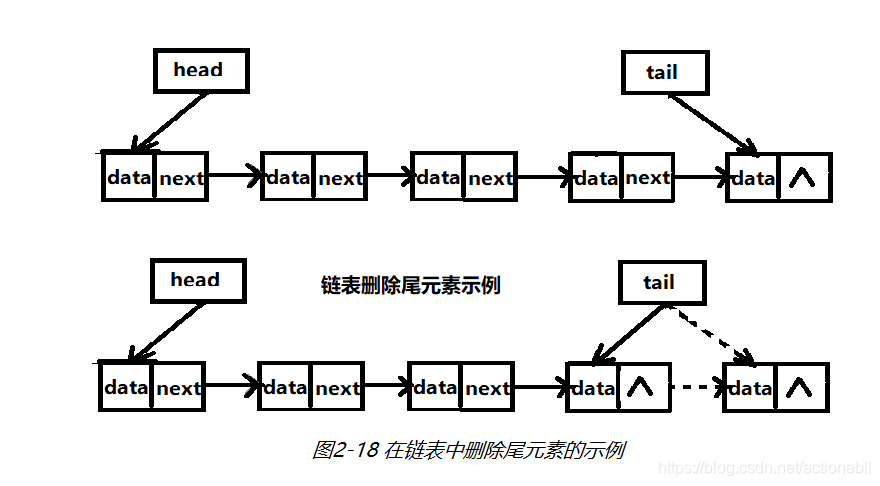
删除中间元素时会相对复杂一些，首先把要删除的节点的之前一个节点的指针指向要删除的节点的下一个节点，接着要把删除节点的指针置空，如图2-19所示。
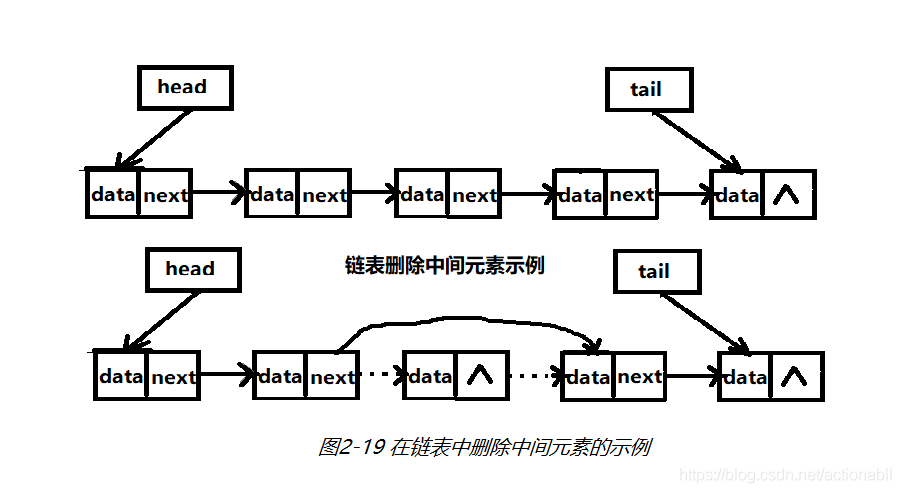
程序代码如下。链表需要两个部分的实现：节点和链表。
首先是节点部分的代码。
package Node;
public class Node {
private int data;
private Node next;
public int getDate() {
return data;
}
public void setData(int data) {
this.data=data;
}
public Node getNext() {
return next;
}
public void setNext(Node next) {
this.next = next;
}
}
节点的代码实现了两个部分，一个是数据，一个是指向下一个节点的属性（这里用了这个类本身作为下一个元素的类型，这应该很好理解）。
下面是链表的代码实现
package Node;
public class Link {
private int size = 0;
private Node first;
private Node last;
/*链表的初始化*/
public Link() {
}
/*链表后部插入
* @param data*/
public void addLast(int data) {
if(size == 0) {
//为空初始化前后元素
fillStart(data);
}else {
Node node = new Node();
node.setData(data);
last.setNext(node);
last = node;//把最后插入的元素设置为链表尾的元素
}
size++;
}
/*链表头部插入
* @param data*/
public void addFirst(int data) {
if(size == 0) {
fillStart(data);
}else {
Node node = new Node();
node.setData(data);
node.setNext(first);//把元素的下一个位置的指针指向头元素
first = node;//把刚插入的元素设置为链表头元素
}
size ++;
}
/*在链表指定的位置后面插入
* @param data 需要插入的数据
* @param index 下标从0开始*/
public void add(int data,int index) {
if(size>index) {
if(size == 0) {
//为空初始化前后元素
fillStart(data);
size++;
}else if(index == 0) {
addFirst(data);
}else if(size == index+1) {
//最后直接调用addLast
addLast(data);
}else {
Node temp = get(index);
Node node = new Node();
node.setData(data);
node.setNext(temp.getNext());
temp.setNext(node);
size++;
}
}else {
throw new IndexOutOfBoundsException("链表没有那么长");
}
}
/*删除链表头元素*/
public void removeFirst() {
if(size == 0) {
throw new IndexOutOfBoundsException("链表没有元素");
}else if(size == 1) {
//只需一个时需要清楚first和last
clear();
}else {
Node temp =first;
first = temp.getNext();
temp = null;//帮组空间回收
size--;
}
}
/*删除链表尾部元素*/
public void removeLast() {
if(size == 0) {
throw new IndexOutOfBoundsException("链表没有元素");
}else if(size == 1) {
//只需一个时需要清楚first和last
clear();
}else {
Node temp = get(size-2);//获取最后元素之前的一个元素
temp.setNext(null);//帮组空间回收
size --;
}
}
/*删除链表中间的元素
* @param index*/
public void removeMiddle(int index){
if(size == 0) {
throw new IndexOutOfBoundsException("链表没有元素");
}else if(size == 1) {
//只剩一个时需要清楚first和last
clear();
}else {
if(index == 0) {
removeFirst();
}else if(size == index -1) {
removeLast();
}else {
Node temp = get(index -1 );//获取要删除的元素之前的一个元素
Node next = temp.getNext();
temp.setNext(next.getNext());
next = null;//帮组空间回收
size--;
}
}
}
/*获取指定下标元素
* @param index
* @return*/
public Node get(int index) {
Node temp = first;
for (int i = 0; i < index; i++) {
temp = temp.getNext();
}
return temp;
}
/*打印所有元素的数据*/
public void printAll() {
//当然也可以用do...while实现
Node temp = first;
System.out.println(temp.getDate());
for (int i = 0; i < size-1; i++) {
temp = temp.getNext();
System.out.println(temp.getDate());
}
}
public int size() {
return size;
}
/*在链表头插入第一个元素时，头、尾元素都是一个元素
* @param data*/
private void fillStart(int data) {
first = new Node();
first.setData(data);
last = first;
}
/*在元素只有一个时清楚first和last元素*/
private void clear() {
first = null;
last = null;
size =0;
}
}
下面是测试代码
package Node;
public class LinkTest {
public static void main(String[] args) {
Link link = new Link();
link.addFirst(2);
link.addFirst(1);
link.addLast(4);
link.addLast(5);
link.add(3, 1);//在下标为1的元素之后插入元素
printAllElements(link);//1,2,3,4,5
link.printAll();//这样打印效率会更高
link.removeFirst();
link.removeLast();
link.removeMiddle(1);
printAllElements(link);//移除了头尾之后，剩下3个元素，移除下标为1的元素，只剩下两个元素2和4
link.removeFirst();
link.removeFirst();
System.out.println(link.size());//从头部全部移出
}
private static void printAllElements(Link link) {
for (int i = 0; i < link.size(); i++) {
System.out.println(link.get(i).getDate());
}
}
}
链表的实现逻辑有点复杂。在程序中可以看到有抛出异常的情况，在中间插入和删除也考虑到index为头和尾的情况，这样避免调用方法失误而导致程序出错。
链表的特点
链表由于本身存储结构的原因，有以下几个特点。
（1）物理空间不连续，空间开销更大。
链表最大的一个特点是在物理空间上可以不连续。这样的优点是可以利用操作系统的动态内存管理，缺点是需要更多的存储空间去存储指针信息。
（2）在运行时可以动态添加。
由于数组需要在初始化时设定长度，所以在使用数组时往往会出现长度不够的情况，这时只能再声明一个更长的数组，然后把旧数组的数据复制进去，在前面栈的事项中已经看到了这一点。
但是若使用链表，则一般不会出现空间不够用的情况。
（3）查找元素需要顺序查找。
通过上面的代码可以看出，查找元素时，需要逐个遍历往后查找元素。其实在测试代码中采用循环队列元素的方法的效率并不高，尤其是当链表很长时，所查找的元素的位置越靠后，效率越低。
在执行删除操作时，也会遇到类似的问题。
（4）操作稍显复杂。
在增加和删除元素时，不但需要处理数据，还需要处理指针。从代码来看，删除最后一个元素时，获取最后一个元素很方便，但是由于操作需要实现倒数第2个元素的next指向设置为空，所以只能从头遍历并获取倒数第2个元素之后再进行删除操作。
链表的适用场景
现在，计算机的空间越来越大，物理空间的开销已经不是我们要关心的问题了，运行效率才是我们在开发中主要考虑的问题。
我们在前面提到，链表除了单向链表，还有双向链表。一般我们会优先使用双向链表，因为多使用的那个指针所占用的空间对于现在的计算机资源来说并不重要。双向链表相对于单向链表的一个优势就是，不管是从头找还是从尾找，操作是一样的。因此对尾元素进行操作时就不用逐个从头遍历了，可以直接从尾向前查找元素。
链表可以在运行时动态添加元素，这对于不确定长度的顺序存储来说很重要。前面介绍的集合（列表）采用数组实现，在空间不够时需要换个更大的数组，然后进行数据复制操作。这时如果采用链表就非常方便了。
链表有什么劣势？劣势就是在查找中间元素时需要遍历。一般而言，链表也经常配合其他结构一同使用，例如散列表、栈、队列等。
一般的程序里可能会使用一个简单的队列进行消息缓冲，而队列的操作只能从头、尾进行，所以此时使用链表（双向链表）去实现就非常方便。
链表的性能分析
一般我们在分析性能时都是以单向链表作为分析对象的。
链表的插入分为三种：头插、尾插和中间插。头、尾插是能够直接插入的，其时间复杂度为O(1)；而中间插需要遍历链表，所以时间复杂度为O(L)，L为插入下标。
链表的删除同样也分为三种：头删、尾删和中间删。头删的时间复杂度为O(1)；中间删同样是O(L)；尾删的时间复杂度则达到了O(N)，N为链表长度。
对于查询来说，时间复杂度是O(L)，L一样是查询下标。
所以对于链表来说，我们可以发现，链表的头插和头删都是O(1)的时间复杂度，这和栈很像，所以栈可以直接使用单向链表实现。
面试举例：如何反转链表
怎么反转链表呢？这个是面试中经常出现的一道题。一般在数据结构或者算法的面试题中，尽量不使用额外的空间去实现，尽管现在的计算机空间很充足，但是面试考察的是对于整体性能的考虑。
方法其实有很多，我们可以一次遍历链表，然后依次使用头插入的方法来达到目的。
下面就是通过反转指针来实现反转链表的代码。
/*反转链表*/
public void reverse() {
Node temp = first;
last = temp;
Node next = first.getNext();
for (int i = 0; i < size-1; i++) {
Node nextNext = next.getNext();//下下个
next.setNext(temp);
temp = next;
next = nextNext;
}
last.setNext(null);
first = temp;
}
这部分代码应该在Link类里，通过反转指针实现链表反转。
接下来我们看看测试代码。
package Node;
public class LinkReverseTest {
public static void main(String[] args) {
Link link = new Link();
link.addLast(1);
link.addLast(2);
link.addLast(3);
link.addLast(4);
printAllElements(link);
link.reverse();
printAllElements(link);
}
private static void printAllElements(Link link) {
for (int i = 0; i < link.size(); i++) {
System.out.println(link.get(i).getDate());
}
}
}
这样可以轻松地完成链表反转。
扫一扫
6万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
