cf1354C，两个几何题

最新推荐文章于 2024-11-12 23:16:35 发布

原创最新推荐文章于 2024-11-12 23:16:35 发布 · 166 阅读

CC 4.0 BY-SA版权

本文探讨了CF1354C系列题目，分别针对偶数和奇数情况下的正多边形，讨论如何计算能放入的最大正方形边长。提供了详细的解题思路与代码实现。

cf1354C1
1400的题
题目大意是给你一个数n且n为偶数，对于边数为2n的正多边形，且每条边的长度都为1，求一个正方形的边长最少为多少才能放进这个正多边形。
注意这里的是n为偶数，下一题为n为奇数，难度直接提升到2000.
cf1354C2
这个题目是n为奇数，其他和前一题都一样
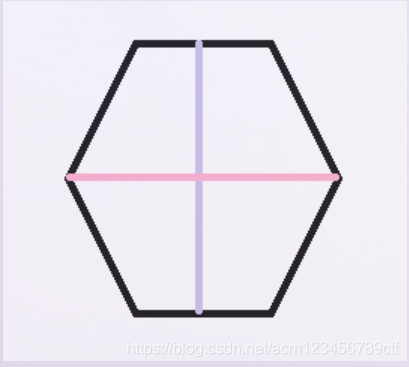
先说当n为奇数时，这个正多边形是一个对称图形，应该说对于每个正多边形都是对称图形，但注意到这里的对称轴是可以对称的边之间的连线也可以说是这个正多边形的高吧，也就是说正方形的边长等于这个高就行了
这两条高即是正方形最短的边长
先放C1的代码吧

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <stack>
#include <cmath>
#include <map>
using namespace std;
typedef long long ll;
#define rep(i, a, n) for(int i = a; i < n; i++)
#define per(i, a, n) for(int i = n-1; i >= a; i--)
#define INF 1ll<<60
const int maxn = 2e5+10;
char s[maxn];
#define PI acos(-1)		//这个就是π
int main(){
    int t;
    scanf("%d", &t);
    while(t--){
        int n;
        scanf("%d", &n);
        //printf("%.10lf\n", PI);
        double r = double(PI/2/n);	//r为一条边对应的中心角度的一半
        double s = tan(r);
        double m = 1.0/s;		//m即为对称轴的长度，也就是高
        printf("%.10lf\n", m);
    }
    return 0;
}

当n为奇数时，这两个对称轴的长度不一样，显然不能直接取更长的那一个对称轴，即要把正方形进行旋转，之后得到的正方形的边长才是最短的。
这两个对称轴长度不一
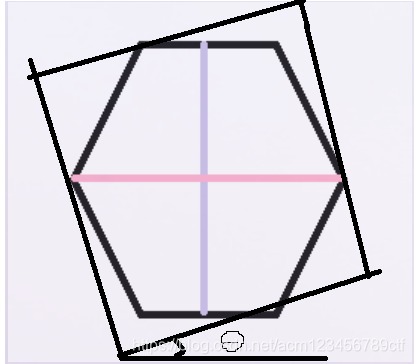
旋转之后的正方形是这样的，差不多那个意思，图有点差，θ角即为正方形旋转的角度，通过一系列的数学运算。。。得到最后的结果θ=(2π-π/2-r*n/2)/2-π/2，乍一看很复杂，~~其实就是很复杂~~ ，但最后能得到的结论是θ=1/4的边对应的中心角，惊不惊喜，意不意外。。。。第一个实现的过程看图即可
在这里插入图片描述
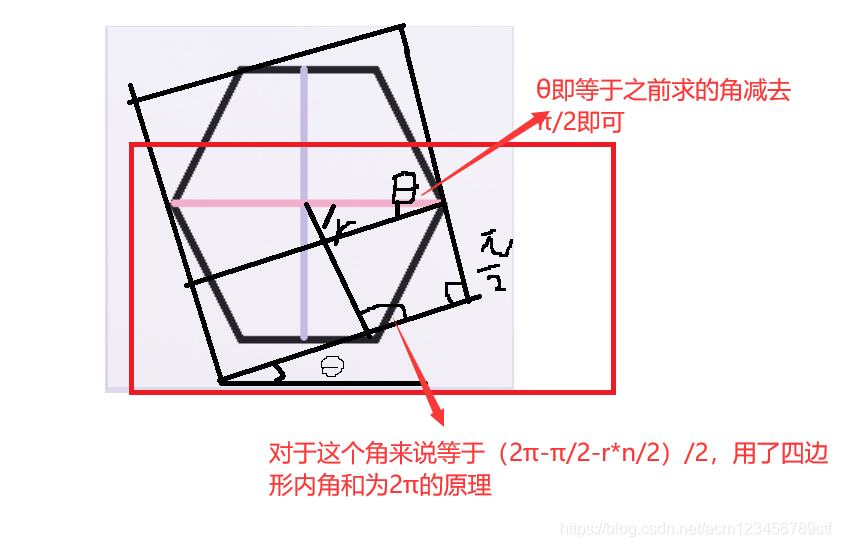
画图有点辣鸡
最后的代码也就显而易见了

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <stack>
#include <cmath>
#include <map>
using namespace std;
typedef long long ll;
#define rep(i, a, n) for(int i = a; i < n; i++)
#define per(i, a, n) for(int i = n-1; i >= a; i--)
#define INF 1ll<<60
const int maxn = 2e5+10;
char s[maxn];
#define PI acos(-1)
int main(){
    int t;
    scanf("%d", &t);
    while(t--){
        int n;
        scanf("%d", &n);
        double r = double(PI/n);	//一条边对应的中心角
        double r1 = r/2.0;			//中心角的一半
        double l = 1.0/sin(r1);		//其中更长的一个对称轴
        double x = l*cos(r1/2.0);	//中心角的1/4
        printf("%.10lf\n", x);
    }
    return 0;
}