本文详细介绍了深度优先搜索（DFS）和广度优先搜索（BFS）算法，包括它们在二叉树中的应用及递归与栈、队列的实现方式。DFS是一种沿树深度遍历的搜索策略，而BFS则采用宽度优先的方式搜索。两种算法都有各自的适用场景和优缺点，并在图形搜索问题中发挥重要作用。
一、深度优先搜索算法
（英语：Depth-First-Search，DFS）
是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。
因发明“深度优先搜索算法”，约翰·霍普克洛夫特与罗伯特·塔扬在1986年共同获得计算机领域的最高奖：图灵奖。
表可以方便的解决很多相关的图论问题，如最大路径问题等等。
实现方法
①、首先将根节点放入队列中。
②、从队列中取出第一个节点，并检验它是否为目标。
如果找到目标，则结束搜寻并回传结果。
否则将它某一个尚未检验过的直接子节点加入队列中。
③、重复步骤2。
④、如果不存在未检测过的直接子节点。
将上一级节点加入队列中。
重复步骤2。
⑤、重复步骤4。
⑥、若队列为空，表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。
1、二叉树的深度优先搜索（递归实现）：
public static void treeDFS(TreeNode root) {
//当前节点为空直接返回
if (root == null)
return;
//打印当前节点的值
System.out.println(root.val);
//然后递归遍历左右子节点
treeDFS(root.left);
treeDFS(root.right);
}
作者：sdwwld
链接：https://leetcode-cn.com/problems/binary-tree-paths/solution/257-er-cha-shu-de-suo-you-lu-jing-tu-wen-jie-xi-by/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
2、实例（递归实现）：
LeetCode 257——二叉树的所有路径
给定一个二叉树，返回所有从根节点到叶子节点的路径。
class Solution{
public List<String> binaryTreePaths(TreeNode root){
List<String> paths = new ArrayList<String>();
constructPaths(root, "", paths);
return paths;
}
public void constructPaths(TreeNode root, String path, List<String> paths){
if(root != null){
StringBuffer pathSB = new StringBuffer(path);
pathSB.append(Integer.toString(root.val));
if(root.left == null && root.right == null){
paths.add(pathSB.toString());
}else{
pathSB.append("->");
constructPaths(root.left, pathSB.toString(), paths);
constructPaths(root.right, pathSB.toString(), paths);
}
}
}
}
但是，如果不是使用StringBuffer，而是使用“+”：
class Solution{
public List<String> binaryTreePaths(TreeNode root){
List<String> paths = new ArrayList<String>();
constructPaths(root, "", paths);
return paths;
}
public void constructPaths(TreeNode root, String path, List<String> paths){
if(root != null){
// StringBuffer pathSB = new StringBuffer(path);
// pathSB.append(Integer.toString(root.val));
path = path + root.val;
if(root.left == null && root.right == null){
paths.add(path);
}else{
path = path + "->";
constructPaths(root.left, path, paths);
constructPaths(root.right, path, paths);
}
}
}
}
相比new StringBuffer()，耗时多了，但是空间少了，即时间复杂度增加了，但是空间复杂度降低了。
3、二叉树的深度优先搜索（栈实现）：
public static void treeDFS(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
stack.add(root);
while (!stack.empty()) {
TreeNode node = stack.pop();
System.out.println(node.val);
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
}
作者：sdwwld
链接：https://leetcode-cn.com/problems/binary-tree-paths/solution/257-er-cha-shu-de-suo-you-lu-jing-tu-wen-jie-xi-by/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
4、实例（栈实现）：
public List<String> binaryTreePaths(TreeNode root) {
List<String> res = new ArrayList<>();
if (root == null)
return res;
//栈中节点和路径都是成对出现的，路径表示的是从根节点到当前
//节点的路径，如果到达根节点，说明找到了一条完整的路径
Stack<Object> stack = new Stack<>();
//当前节点和路径同时入栈
stack.push(root);
stack.push(root.val + "");
while (!stack.isEmpty()) {
//节点和路径同时出栈
String path = (String) stack.pop();
TreeNode node = (TreeNode) stack.pop();
//如果是根节点，说明找到了一条完整路径，把它加入到集合中
if (node.left == null && node.right == null) {
res.add(path);
}
//右子节点不为空就把右子节点和路径压栈
if (node.right != null) {
stack.push(node.right);
stack.push(path + "->" + node.right.val);
}
//左子节点不为空就把左子节点和路径压栈
if (node.left != null) {
stack.push(node.left);
stack.push(path + "->" + node.left.val);
}
}
return res;
}
作者：sdwwld
链接：https://leetcode-cn.com/problems/binary-tree-paths/solution/257-er-cha-shu-de-suo-you-lu-jing-tu-wen-jie-xi-by/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
二、广度优先搜索算法
（英语：Breadth-First-Search，缩写为BFS）
又译作宽度优先搜索，或横向优先搜索，是一种图形搜索算法。简单的说，BFS是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。广度优先搜索的实现一般采用open-closed表。
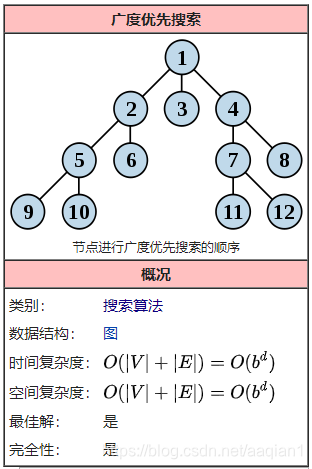
BFS是一种盲目搜索法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能地址，彻底地搜索整张图，直到找到结果为止。BFS并不使用经验法则算法。
从算法的观点，所有因为展开节点而得到的子节点都会被加进一个先进先出的队列中。一般的实现里，其邻居节点尚未被检验过的节点会被放置在一个被称为 open 的容器中（例如队列或是链表），而被检验过的节点则被放置在被称为 closed 的容器中。（open-closed表）
实现方法
①、首先将根节点放入队列中。
②、从队列中取出第一个节点，并检验它是否为目标。
如果找到目标，则结束搜索并回传结果。
否则将它所有尚未检验过的直接子节点加入队列中。
③、若队列为空，表示整张图都检查过了——亦即图中没有欲搜索的目标。结束搜索并回传“找不到目标”。
④、重复步骤2。
1、二叉树的广度优先搜索（队列实现）：
public static void levelOrder(TreeNode tree) {
if (tree == null)
return;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(tree);//相当于把数据加入到队列尾部
while (!queue.isEmpty()) {
//poll方法相当于移除队列头部的元素
TreeNode node = queue.poll();
System.out.println(node.val);
if (node.left != null)
queue.add(node.left);
if (node.right != null)
queue.add(node.right);
}
}
作者：sdwwld
链接：https://leetcode-cn.com/problems/binary-tree-paths/solution/257-er-cha-shu-de-suo-you-lu-jing-tu-wen-jie-xi-by/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
2、广度优先搜索实例
public List<String> binaryTreePaths(TreeNode root) {
List<String> res = new ArrayList<>();
if (root == null)
return res;
//队列，节点和路径成对出现，路径就是从根节点到当前节点的路径
Queue<Object> queue = new LinkedList<>();
queue.add(root);
queue.add(root.val + "");
while (!queue.isEmpty()) {
TreeNode node = (TreeNode) queue.poll();
String path = (String) queue.poll();
//如果到叶子节点，说明找到了一条完整路径
if (node.left == null && node.right == null) {
res.add(path);
}
//右子节点不为空就把右子节点和路径存放到队列中
if (node.right != null) {
queue.add(node.right);
queue.add(path + "->" + node.right.val);
}
//左子节点不为空就把左子节点和路径存放到队列中
if (node.left != null) {
queue.add(node.left);
queue.add(path + "->" + node.left.val);
}
}
return res;
}
作者：sdwwld
链接：https://leetcode-cn.com/problems/binary-tree-paths/solution/257-er-cha-shu-de-suo-you-lu-jing-tu-wen-jie-xi-by/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
扫一扫
2163
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
