C语言 数据在内存中的存储详解

---

前言

这一章主要讲一下整数、浮点数在内存中的存储以及大小端字节序。
1步带你搞懂大小端

---

一、整数在内存中的存储

整数的2进制表示方法有三种：原码、反码、补码
原码：直接将正负数翻译成二进制就是原码
反码：原码取反
补码：反码加1
对于整形来说，数据在内存中的存储其实是补码。

二、大小端字节序和字节序判断

int a =0x11223344;
11是高位字节，44是低位字节
在内存中从左向右地址是由低到高。
小端存储：低位字节放在低地址处。a（小端）44332211
大端存储：低位字节放在高地址处。a（大端）11223344

浮点数在内存中的存储

浮点类型有：float、double、long double
根据国际标准IEEE（电⽓和电⼦⼯程协会） 754，任意⼀个⼆进制浮点数V可以表⽰成下⾯的形式：
V = (−1)^S ∗ M ∗ 2^E
•-(1)^S 表⽰符号位，当S=0，V为正数；当S=1，V为负数
•M 表⽰有效数字，M是⼤于等于1，⼩于2的
• 2^E 表⽰指数位
例：
十进制的5.0，写写成二进制是101.0，相当于1.01*2²。
S=0,M=1.01,E=2
float类型：

double类型：

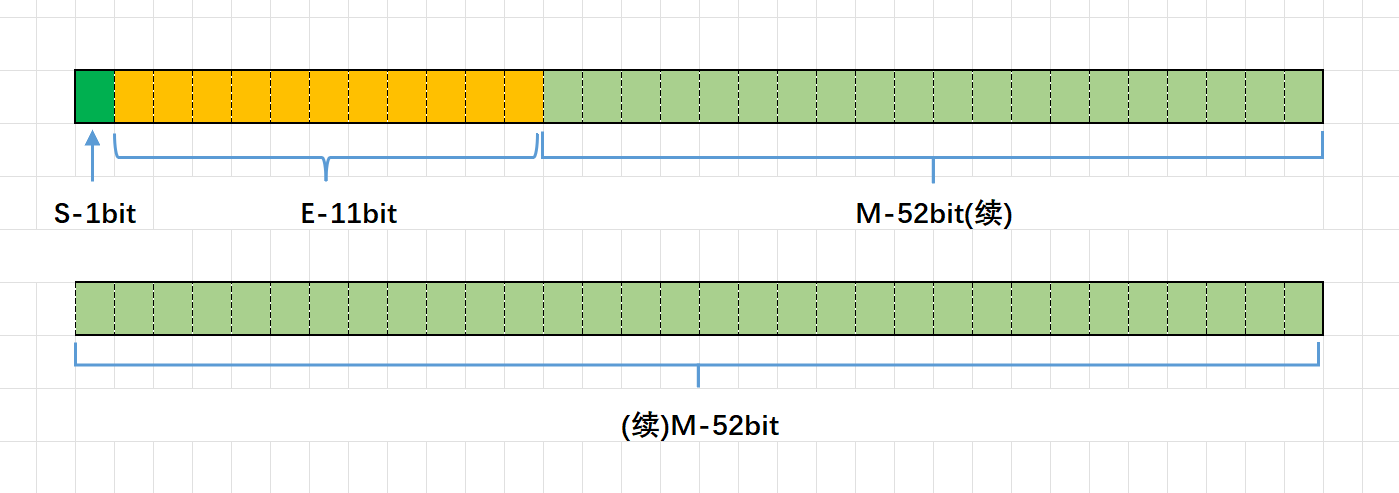
浮点数存储中的M

前面说过1<=M<2，在存储时会把前面的1舍去，只存储后面的小数部分，读取时把1加上去，因为这样会省去一个位置

浮点数存储中的E

首先E是一个无符号整数（unsigned int ）
因为科学计数法的E有负数，所以规定E的真实值必须再加上一个中间数
E为8位时（0~255）+127
E为16位时（0~2047）+1023

1. E为全0时
   E=真实值加127 2^-127无限接近于0
   0 00000000 00100000000000000000000

2. E为全1时
   E=真实值加127
   0 11111111 00010000000000000000000
   真实值无限接近于正无穷

3. E不为全0也不为全1（常规情况）

---

总结

如果有什么不懂的可以私信我或者评论区留言