力学流体simple

问题

顶盖驱动流动

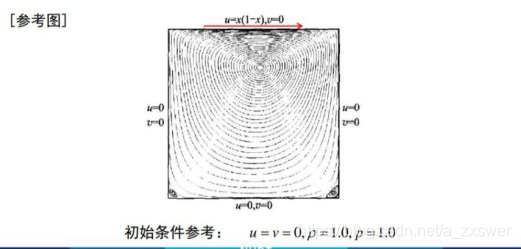
问题描述

假设 的方腔内充满粘性不可压缩流体，左、右、下壁固定，上壁以 运动， 方腔内初始时刻压力和密度为它周围壁面（左右壁面和底面）固定不动，上壁面以量纲为一的速度沿着上壁面方向自左向右运动。方腔如图1所示。

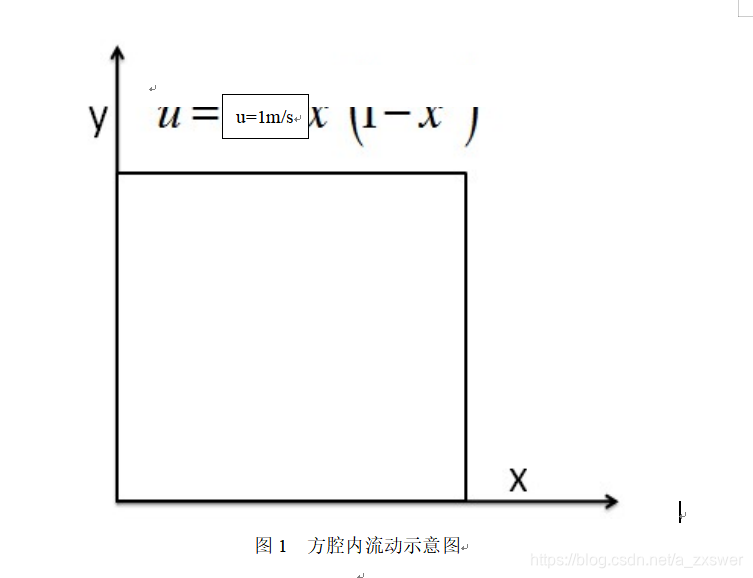
图1 方腔内流动示意图

基本方程组、初始条件和边界条件
设流体是黏性流体。二维方腔流动问题的动量方程为：

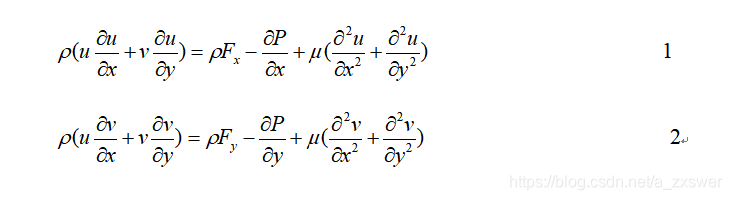
连续方程为：

                                        （3）

其中为水平方向的流速，为方向的流速，为黏度
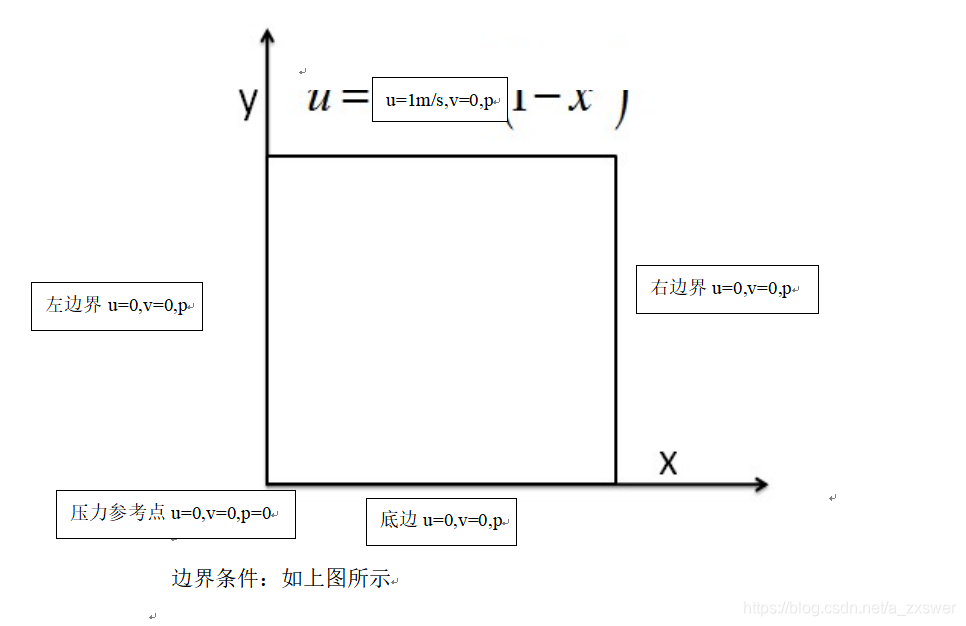
初始条件：方腔上壁面以量纲为一的速度沿着上壁面方向自左向右运动。

离散动量方程

 本算例采用求解不可压缩流动的经典算法，即SIMPLE算法，求解方腔内粘性不可压缩流体运动的定常解。

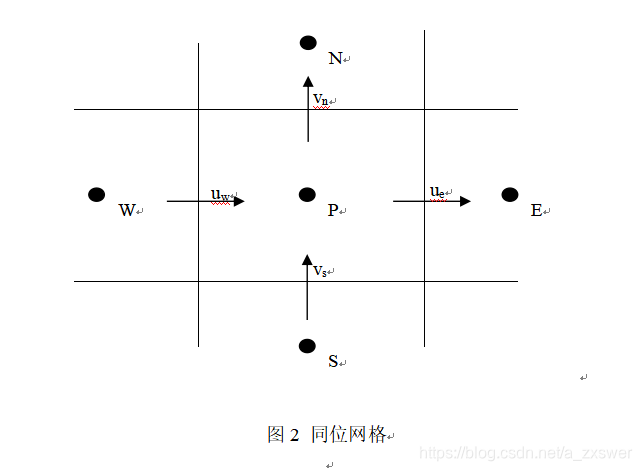
同位网格如图2所示，

图2 同位网格

在同位网格上，将u动量方程 对控制容积P作积分，可得到：

对于对流项，采用三阶迎风型离散格式进行分析，当时，通过、和三个节点值拟合曲线来计算主控制单元左侧界面参数。通过节点、和三个节点值拟合曲线来计算主控制单元右侧界面参数。当，则分别通过节点、、和、、三个节点值计算主控制单元左、右两侧界面参数和。根据上述计算原则，可以得到界面参数计算公式如下：

以上是动量方程的离散。

SIMPLE算法基本思想

SIMPLE算法是一种解决压力-速度耦合问题的“半隐式”算法。首先给定n时刻猜测的速度场，用于计算离散动量方程中的系数和常数项。给定n时刻猜测的压力场估计值，迭代求解离散动量方程，得到n+1时刻速度场的估计值，速度场的估计值满足如下离散方程。

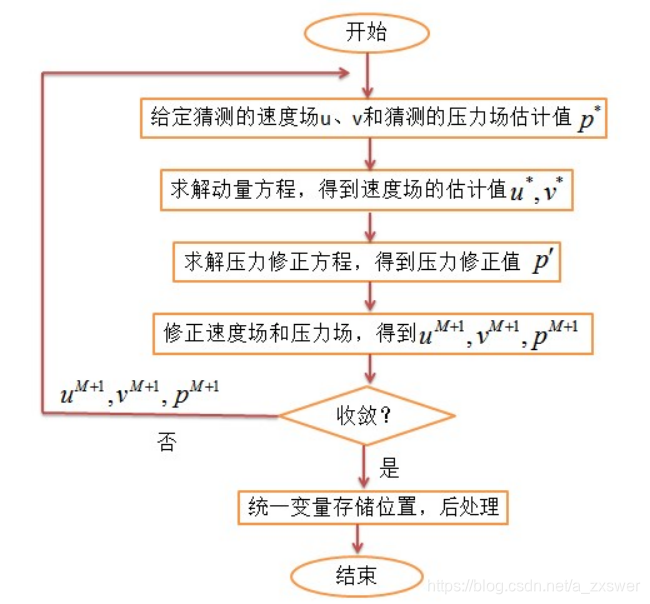
Simple算法的流程图：

源码链接：

https://download.youkuaiyun.com/download/a_zxswer/20011730.