GIGNet: A Graph-in-Graph Neural Network for Automatic Modulation Recognition

GIGNet: A Graph-in-Graph Neural Network for Automatic Modulation Recognition

https://ieeexplore.ieee.org/abstract/document/10896841

由于本文篇幅较短，缺少细节部分，有些内容是根据自己的理解进行补充，可能存在误解，细节部分见PPT附件

一.概述

1. GIGNet 流程简述

1. 单样本内部的图表示

   • 对每条信号（单个样本），先将其采样点映射为图（采样点 → 节点），并通过多级 Graph-level GNN 提取局部与全局特征。
   • 最终会得到一个对整条信号的图级表示向量，记作 $({\mathbf{f}}_i)$。如果我们一次性处理了 $(N)$ 条信号，则会得到一个矩阵

   $ F_{\mathrm{in}} = \begin{bmatrix} \mathbf{f}_1 \ \mathbf{f}_2 \ \vdots \ \mathbf{f}_N \end{bmatrix} \in \mathbb{R}^{N\times d_f},$

   其中第 $(i)$ 行对应第 $(i)$ 条信号的特征表示。

2. 样本之间的图构造（Graph Construction Operation）

   • 这一步为了利用“批量样本之间”的关联信息，把每条信号视为一个节点，构造“样本-样本”图。
   • 具体做法：对 $(F_{\mathrm{in}})$ 里的每对信号 $((i,j))$ 计算它们的 L1 距离，得到距离矩阵 $(D)$，再转化为相似度矩阵并稀疏化、归一化，最终得到邻接矩阵 $(\tilde{A})$。

3. 节点级 GNN（Node-level GNN）

   • 在这个阶段，$(N)$ 条信号就是 $(N)$ 个节点，邻接矩阵 $(\tilde{A})$ 表示它们之间的相似度边权。
   • 将 $(F_{\mathrm{in}})$ 作为初始节点特征输入图卷积（GraphConv），得到一个新的特征矩阵

   $F=\text{NodeGNN}(\tilde{A},F_{\mathrm{in}}).$

   在这里，每个节点（即每条信号）可从最相似的其他节点处获取信息，进一步丰富其特征表示。

4. 分类模块

   • 最终得到的 $(F\in {\mathbb{R}}^{N\times d^{\prime }})$ 就是所有样本在“样本-样本”图上的最后表示。
   • 通常会加一个或多个全连接层（MLP）进行分类：对第 $(i)$ 个样本对应的特征 $(F_i)$ 进行预测，得到其调制类型。

---

2. 样本之间的邻接矩阵如何确定

1. 基于内部特征距离

   • 先对每条信号的内部图表示向量（$({\mathbf{f}}_i\in {\mathbb{R}}^{d_f})$）进行距离计算：

     $D_{ij}=\Vert {\mathbf{f}}_i-{\mathbf{f}}_j{\Vert }_{L1}={\sum }_{l=1}^{d_f}|f_i^l-f_j^l|.$

   • 这样得到 $(D\in {\mathbb{R}}^{N\times N})$，表示任意两条信号之间的差异。

2. 转化为相似度并稀疏化

   • 将距离矩阵 $(D)$ 转化为相似度矩阵 $(A)$:

     $Aij=1\hspace{0.17em}1+Dij.A_{ij}=\frac{1}{1+D_{ij}}.$

   • 选取每行 Top-$(M)$ 的邻居并归一化，得到最终稀疏邻接矩阵 $(\tilde{A})$。

---

3. 多个样本在一个 GNN 中如何分类

1. 多个样本 → 一个图
   • 在 Node-level GNN 阶段，我们把批量中的 $(N)$ 个样本当作图中的 $(N)$ 个节点；邻接矩阵 $(\tilde{A})$ 则是 $(N\times N)$。
   • 每个节点都会通过图卷积，与它的邻居进行特征交换，得到新的表示。
2. 最后的特征矩阵 $(F)$
   • 形状为 $({\mathbb{R}}^{N\times d^{\prime }})$，其中第 $(i)$ 行 $(F_i)$ 就是第 $(i)$ 个样本更新后的特征。
   • 这个特征融合了“内部图”学到的信息 + “样本间相似度”带来的补充信息。
3. 分类内容
   • 通常在 $(F)$ 的基础上加一个或多个全连接层（MLP），对每个样本做调制类型预测。
   • 在训练时，通过比较预测标签与真实标签来计算损失并反向传播，端到端地更新所有网络参数。

---

结论：

• 样本之间的邻接矩阵是根据它们在内部特征空间中的 L1 距离构造的。
• 多个样本共同放到一个 Node-level GNN 中时，最终输出 $(F)$ 中的每行依然对应每个样本的特征，随后可用常规分类层来做最终的调制识别。

---

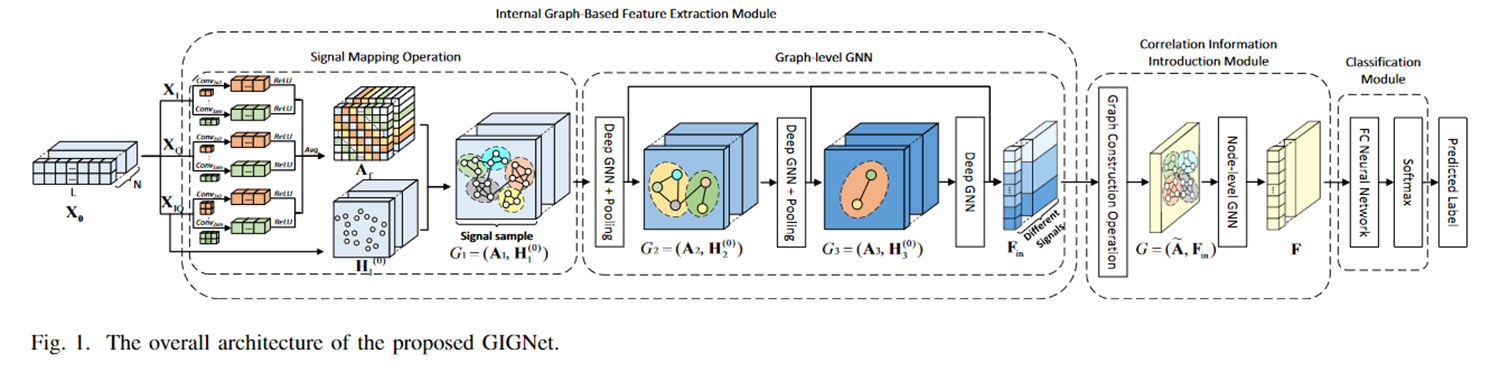
二. 细节

GIGNet 的整体流程可以分为三大模块：

1. 内部图特征提取模块（Internal Graph-Based Feature Extraction Module）
   • 信号映射操作 (Signal Mapping Operation)
   • 图级 GNN (Graph-level GNN)
2. 相关性信息引入模块（Correlation Information Introduction Module）
   • 图构造操作 (Graph Construction Operation)
   • 节点级 GNN (Node-level GNN)
3. 分类模块 (Classification Module)

在这三个模块中，模型先对单个信号进行图表示提取，再在批量样本之间构造新的“样本-样本”图，从而实现多级关联信息的提取，最终进行调制类型分类。

---

2. 内部图特征提取模块

2.1 信号映射操作 (Signal Mapping Operation)

• 输入：原始 IQ 信号 $({\mathbf{X}}^I,{\mathbf{X}}^Q,{\mathbf{X}}^{IQ}$)
• 过程：
  1. 从实部、虚部、以及 IQ 联合通道中提取「相关性序列 $({\varphi }_s^I,{\varphi }_s^Q,{\varphi }_s^{IQ}$ )。
  2. 将这些序列映射成邻接矩阵 $(A^I,A^Q,A^{IQ}$)，再融合为 $(A_f$ )。
  3. 将每个信号的采样点视为图的节点，初始节点特征（例如实部+虚部）用来构造节点特征矩阵。
• 输出：
  • 融合邻接矩阵 $(A_f\in {\mathbb{R}}^{N\times L\times L}$ )（若批大小为 $(N$)，每个信号长度为 $(L$)）
  • 初始节点特征矩阵（如 $(H_1^{(0)}$ )）

目的：将单个信号的采样点关系转化为图结构，以提取局部与全局特征。

2.2 图级 GNN (Graph-level GNN)

• 输入：
  • 融合邻接矩阵 $(A_f$)
  • 初始节点特征矩阵 $(H_1^{(0)}$)
• 过程：
  1. 三个并行的深度 GNN（每个有 $(K$) 个残差 GNN Block）对图进行特征提取；
  2. 每个并行分支在不同尺度上学习图结构信息；
  3. DIFFPool 等图池化操作可进一步压缩节点数，获得分层次表示。
• 输出：
  • 多尺度图特征 ( { H p ( K ) } (\{H_p^{(K)}\} ({Hp(K)​})（$(p=1,2,3$)）
  • 最后通过 Readout(·) 和 Concat(·) 得到多尺度内部图特征矩阵 $(F_{\mathrm{in}}\in {\mathbb{R}}^{N\times d_f}$)

目的：对「单个信号」的图表示进行深度特征提取，最终得到一个高维向量来描述每条信号。

---

3. 相关性信息引入模块

3.1 Graph Construction Operation

• 输入：
  • 上一步得到的 $(F_{\mathrm{in}}\in {\mathbb{R}}^{N\times d_f}$)
    • 这里，每行对应一个信号在内部图级 GNN 提取后的最终表示。
• 操作内容：
  1. 节点与节点之间的内容：此时每个“节点”代表一条“信号”（不是采样点），因此是“样本-样本”之间的图。
  2. 计算距离矩阵 $(D\in {\mathbb{R}}^{N\times N}$)：
     $[D_{ij}={\sum }_{l=1}^{d_f}|v_l^i-v_l^j|(\text{L1 距离})]$
     这是样本间特征向量的距离矩阵，表示第 $(i$) 条信号与第 $(j$) 条信号在特征空间中的差异。
  3. 将距离矩阵 $(D$) 转换为相似性矩阵 $(A$)：
     $[A_{ij}=\frac{1}{1+D_{ij}},]$
     并选取 Top-M 相似的邻居，最终归一化得到 $(\tilde{A}$)。
• 输出：
  • 邻接矩阵 $(\tilde{A}\in {\mathbb{R}}^{N\times N}$)，每个信号视为一个节点，权重表示两个信号间的关联度。

目的：根据不同信号在内部特征空间的距离，构造一张新的“信号-信号”图，便于后续聚合相关信息。

3.2 节点级 GNN (Node-level GNN)

• 输入：
  • $(\tilde{A}\in {\mathbb{R}}^{N\times N}$ )：表征信号间相似度的邻接矩阵
  • 初始节点特征 $(H^{(0)}$)（这里即 $(F_{\mathrm{in}}$)），每个信号是一个节点
• 过程：
  1. 多层图卷积（GraphConv），逐层将相似信号的特征进行加权聚合；
  2. 使得每条信号都能从最相关的其他信号中汲取额外信息。
• 输出：
  • 最终特征矩阵 $(F\in {\mathbb{R}}^{N\times d(3)}$)，包含了信号间相关性的信息。

目的：进一步利用“批量信号间”的关联，强化每条信号在特征空间的可分性，提高分类精度。

---

4. 分类模块 (Classification Module)

• 输入：节点级 GNN 的最终输出 $(F\in {\mathbb{R}}^{N\times d(3)}$)
• 过程：
  • 常规做法是接一个或多个全连接层（MLP），并加上激活函数 Softmax 等，进行多类别调制类型预测。
• 输出：预测的调制类型（或概率分布）

目的：完成具体的分类任务，输出最终调制识别结果。

---

5. 关键问题解答

5.1 节点的特征向量会变化吗？如何优化？

• 节点特征是否会变化：会的。
  • 在图神经网络的每一层，节点特征都会通过邻接矩阵的加权聚合以及可学习的参数进行更新。例如：
    $[H^{(k)}=\text{GraphConv}(A,H^{(k-1)}),]$
    其中 $(H^{(k)}$) 表示第 $(k$) 层输出的节点特征矩阵。
• 如何优化：
  • 这是一个端到端可训练的模型。整体网络（包括图卷积层、全连接层等）会在训练阶段通过反向传播（BP）进行参数更新。通常以交叉熵损失等分类损失作为目标函数，利用梯度下降（如 Adam 优化器）来优化所有可学习参数。

5.2 $(F_{in}$) 是什么内容？针对整个样本还是针对一个节点？

• $(F_{in}$ )：多尺度内部图特征矩阵，形状一般是 $({\mathbb{R}}^{N\times d_f}$)。
  • 行 (N)：对应批量中的每条“信号样本”；
  • 列 ($d_f$)：对应图级 GNN 提取出的特征维度。
• 因此，$(F_{in}$ ) 并不是针对单个节点（采样点），而是针对整条信号（每条信号得到一个向量），在批次维度上堆叠形成 $(N$) 行。

5.3 Graph Construction Operation 操作的是什么？节点与节点之间，还是样本与样本之间？

• 在这个模块，每条信号就是一个节点。因此它实际上是“样本-样本”的图。
• 不同于最初的“信号映射操作”，后者是在一条信号的内部采样点之间构建图；而“Graph Construction Operation”是把整个批次的信号当作节点，计算它们之间的相似度。

5.4 计算的距离矩阵是什么矩阵？是谁的距离？

• 距离矩阵 $(D$) 用来衡量不同信号之间的差异：
  • 行/列索引分别对应第 $(i$)、第 $(j$) 条信号；
  • 值 $(D_{ij}$) 表示第 $(i$) 条信号与第 $(j$) 条信号在特征向量上的 L1 距离。
• 这与最初单个信号的采样点之间的距离矩阵不同——这里是专门针对批量信号做的距离计算。

---

6. 如何进行整体优化？

• 端到端训练：
  1. 将原始信号输入网络，通过“内部图特征提取模块”得到 $(F_{in}$)。
  2. “相关性信息引入模块”再构造样本-样本图，并做节点级 GNN 聚合。
  3. 输出到分类器得到预测标签，与真实标签比对计算损失 (如交叉熵)。
  4. 对整个网络参数（包括图卷积、全连接、甚至图构造中可学习部分）进行反向传播更新。
• 目标：最小化分类损失、最大化识别准确率。

---

7. 总结

1. 每一步的输入输出

   • 信号映射操作：输入 IQ 信号，输出图 (采样点-采样点)；
   • 图级 GNN：输入融合邻接矩阵和节点特征，输出多尺度内部图特征 $(F_{in}$)；
   • Graph Construction Operation：输入 $(F_{in})(N\times d_f)$，计算出样本间的距离矩阵 $(D$)，再得到相似度矩阵 $(\tilde{A}$)；
   • 节点级 GNN：输入 $(\tilde{A}$) 和 $(F_{in}$)，输出进一步融合相关性后的特征 $(F$)；
   • 分类模块：输入 $(F$)，输出预测标签。

2. 节点特征会变化吗？

   • 是的，每经过一层 GNN，节点特征都会更新。

3. $(F_{in}$ ) 的含义

   • 对应整个批量样本（N 条信号）的高维特征，形状 $(N\times d_f$)，不是单个节点的特征。

4. Graph Construction Operation 是什么？

   • 针对批量中的“信号-信号”关系构图，而非单条信号内部的“采样点-采样点”关系。

5. 距离矩阵计算的对象

   • 计算的是不同信号（样本）之间的特征距离，用 L1 距离衡量它们的差异。

三. 补充

1. 为什么可以在最后使用样本与样本之间的图进行优化？

1.1 动机：利用样本间的“潜在关联信息”

• 传统做法：大部分分类模型将每个样本（信号）独立地输入网络，彼此之间没有信息交互。
• GIGNet 的做法：在模型的后期阶段（或者说在“第二级”图神经网络模块）里，把“每条信号”当作“图中的一个节点”，通过它们在特征空间的相似度构造“样本-样本”图，然后再用 GNN 做特征聚合。
• 好处：
  1. 信息共享：如果某些信号在特征空间里接近（可能具备相同或相似的调制模式），那么对它们做“图卷积”式的邻居特征聚合，可以让模型“互相佐证”，使本来就相似的样本在表征上更趋于一致，从而在分类边界上更容易区分不同类别。
  2. 对抗噪声：无线信道环境中会有噪声与干扰。个别信号可能因为噪声导致特征不稳定，但如果同一批次其他相似信号的特征足够“清晰”，通过图聚合就能帮助纠正该噪声样本的表示。

简而言之，这一步相当于在特征空间里做了一次“基于距离的关联强化”，让模型在同类样本之间传递判别性信息、在不同类样本之间保留差异。

1.2 理解原理：这类似于“Transductive Learning”或“Batch-level Graph”思路

• 在机器学习中，有一种方法论叫“基于图的半监督/推断”或“跨样本传递（Transductive Learning）”，其核心观点是：

  如果在同一批数据中，某些样本之间在特征空间足够接近，那么它们很可能共享某些标签或有相似的分类边界。

• GIGNet 并不是只用单一信号来判别，它还利用了“该信号在一组信号中的位置关系”。从图学习角度来说，这能带来更好的判别能力——相当于在同一个批次/数据集层面上进行了结构化的特征校正。

---

2. 测试时如何做？为什么也可以这样做？

很多人会疑惑：“训练时可以这么干，那测试（推断）时只拿到单条信号怎么办？” 或者 “我们在真实场景中也是一个一个信号进来，怎么做‘样本-样本’图？”

推测，论文或实际实现通常有以下两种思路（具体以论文作者实现为准，这里给出常见做法）：

1. 批量推断（Batch Inference）
   • 在实际推理时，将一批待测试的信号同时输入网络（就像训练时一样），对这批信号之间的相似度进行计算，并构造“测试样本-测试样本”的图，再用节点级 GNN 去更新特征，最终输出预测结果。
   • 这种方法要求在推断阶段也能“攒”一批待识别的信号放在一起。如果真实场景允许“批处理”，就可以直接复用训练阶段的流程。
2. 在线推断 + “缓冲区”构图
   • 如果真实场景必须实时到达就处理，也可以在模型内部维护一个“滑动窗口”或“缓冲区”来收集一定数量的最近到达的信号，构造当前批次的图，然后进行一次推理。这样，每条新信号在被识别的同时也能和窗口内其他信号做图关联。
   • 当然，这种方法在严格实时性要求下会带来延迟，需要在“识别性能提升”和“实时性”之间平衡。

小结：不管是哪种方法，核心点在于：

1. 测试阶段依旧可以构造一个“批”，在那个批里做相似度计算；
2. 只要保证测试阶段的图构造方式（邻居选择、相似度度量等）与训练时是一致的，就能让模型在推断时同样获得“样本-样本”关联带来的好处。

---

3. 为什么可以从周围“关联比较密切”的样本进行优化？

3.1 特征空间的邻居就是潜在“同类”

• 在 GIGNet 的节点级 GNN 里，你会先算出一个距离矩阵 DD（或者相似度矩阵 AA），选择 Top-M 邻居并归一化得到最终的邻接矩阵 A~\tilde{A}。
• 这意味着，如果某个信号与另一个信号在特征空间的距离很小（即它们特征极其相似），就会被判定为邻居，继而在图卷积层里进行信息交互。
• 假设前提：同一调制类别的信号，在高维特征空间中应当彼此接近。这样，图卷积能让它们“互相强化”正确的判别信息；如果有某些信号是其他类别，则在图结构中可能与之关联度低（或没有边），不会把错误信息传递过来。

3.2 提高鲁棒性与一致性

• 当一个样本的神经网络特征受噪声或难例影响而不够稳定时，其在距离度量中往往还会与某些真实同类样本有较强的联系。这些同类样本在多层 GNN 的聚合过程中，可以帮助校正或补足该有噪声的样本，从而在最终判别时更具稳健性。
• 换句话说，这是让网络在训练和推理时都充分利用“批内”或“群体内”的相关性，从而获得更好的泛化性能。

---

4. 总结

1. 在最后进行“样本-样本”图优化
   • 这一步相当于一次“跨样本的特征校正”和“结构化信息传播”，让相似样本之间互相加强表征，从而提升分类效果。
2. 推理时如何进行
   • 通常也会用同样的方法构造一批测试信号间的图，然后做 GNN 聚合；或通过维护一个滑动窗口/小批次缓冲来模拟批量推理。
   • 只要能在测试阶段也形成“小批量”的信号集合，就可以像训练一样利用样本间的邻接关系。
3. 为什么可以从“相似邻居”中受益
   • 因为在特征空间里相似度高的往往是同类或相似的样本，彼此的特征在 GNN 聚合后会更具判别力；对于噪声样本，这也是一个校正机制。

从算法视角来看，这是对样本间潜在关联的充分挖掘，也是图学习、度量学习等思路应用在调制识别领域的一种体现。只要你能够在测试或推断时也批量地（或者成组地）组织信号，就可以将它们之间的关联纳入到推断过程中，实现比“单样本独立分类”更高的识别精度。