SDOI2017 数字表格

最新推荐文章于 2025-12-15 13:40:30 发布

转载最新推荐文章于 2025-12-15 13:40:30 发布 · 79 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/LiGuanlin1124/p/10049858.html

文章标签：

#数据结构与算法

本文介绍了一种使用反演算法求解斐波那契数列的高效方法，通过预先计算并存储关键数值，实现了对大量询问的快速响应。适用于处理大规模数据集，特别是当n和m值较大时，能够有效降低计算复杂度。

题目描述：

f为斐波那契数列。

T组询问，每次给出表格的n、m。表中(i,j)为gcd(i,j)，求表中所有数之积mod 1e9+7的值。

T<=1e5,n,m<=1e9

题解：

反演。

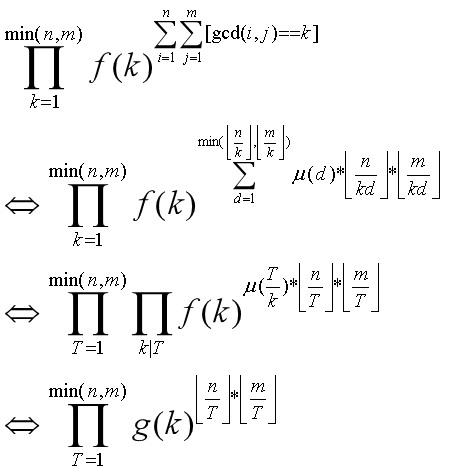
代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 1000500
#define MOD 1000000007
#define ll long long
int t,n,m;
int pri[N],cnt,mu[N];
bool vis[N];
ll f[N][2],g[N],G[N][2];
ll fastpow(ll x,ll y)
{
    ll ret = 1ll;
    while(y)
    {
        if(y&1)ret=ret*x%MOD;
        x=x*x%MOD;
        y>>=1;
    }
    return ret;
}
ll inv(ll x)
{
    return fastpow(x,MOD-2);
}
void init()
{
    mu[1]=1;
    f[1][0]=f[1][1]=1;
    g[1]=1;
    for(int i=2;i<=1000000;i++)
    {
        f[i][1]=(f[i-1][1]+f[i-2][1])%MOD;
        f[i][0]=inv(f[i][1]);
        if(!vis[i])
        {
            pri[++cnt]=i;
            mu[i]=-1;
        }
        for(int j=1;j<=cnt&&i*pri[j]<=1000000;j++)
        {
            vis[i*pri[j]]=1;
            if(i%pri[j])mu[i*pri[j]]=-mu[i];
            else break;
        }
        g[i]=1;
    }
    G[0][1]=G[0][0]=1;
    for(int i=1;i<=1000000;i++)
    {
        if(!mu[i])continue;
        for(int j=1;i*j<=1000000;j++)
        {
            (g[i*j]*=f[j][mu[i]>0?1:0])%=MOD;
        }
    }
    for(int i=1;i<=1000000;i++)
    {
        G[i][1]=G[i-1][1]*g[i]%MOD;
        G[i][0]=inv(G[i][1]);
    }
}
int main()
{
    init();
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&m);
        if(n>m)swap(n,m);
        ll ans = 1ll;
        for(int i=1,nxt;i<=n;i=nxt+1)
        {
            nxt = min(n/(n/i),m/(m/i));
            ll tmp = G[nxt][1]*G[i-1][0]%MOD;
            ans=ans*fastpow(tmp,1ll*(n/i)*(m/i)%(MOD-1))%MOD;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

转载于:https://www.cnblogs.com/LiGuanlin1124/p/10049858.html