降维 之 流形学习 降维法

之前总觉得流形是一个很奇特的东西。想不明白是啥，没有具体的概念，到现在才稍微有一些明白。

这里分享一些自己的见解。

 

概念上，流形是 在局部上与欧氏空间同胚的空间。

这句话我的理解是，在局部里，计算两样本之间的距离，高维和低维是一样能用欧式距离来计算的。

 

这就给降维带来 了启发： 当低维流形嵌入到高维空间时，虽然高维空间异常复杂，但是在局部还是有欧氏空间的性质，因此 ，可以在局部建立起高维空间和 低维空间 之间的映射，然后推广到全局。这就完成了降维操作。

 

• 这次介绍两种利用刚才描述的性质进行降维的方法：
• 1.等度量嵌入 （Isomap）
• 2.局部线性嵌入 （LLE）

 

由于高维空间中的直线距离在低维流形嵌入中是不可达的，（在高维空间直接计算直线距离是有问题的）

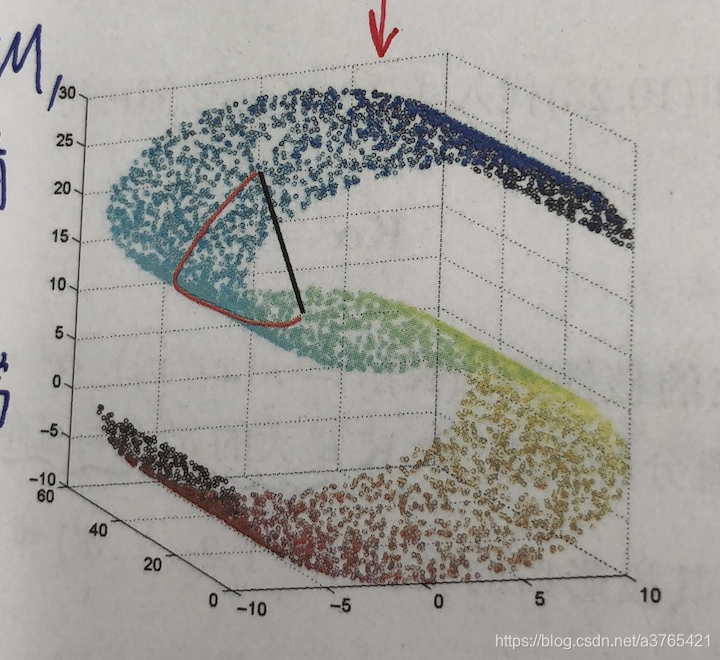
这里我们把流形映射到三维空间的 某S形曲面上，

黑色的直线就是我们在此空间中的企图：直接计算直线距离，这是不对的。

正确的距离计算应是是遵循着红线（称测底线）。

 

因此，我们用近邻距离来近似：

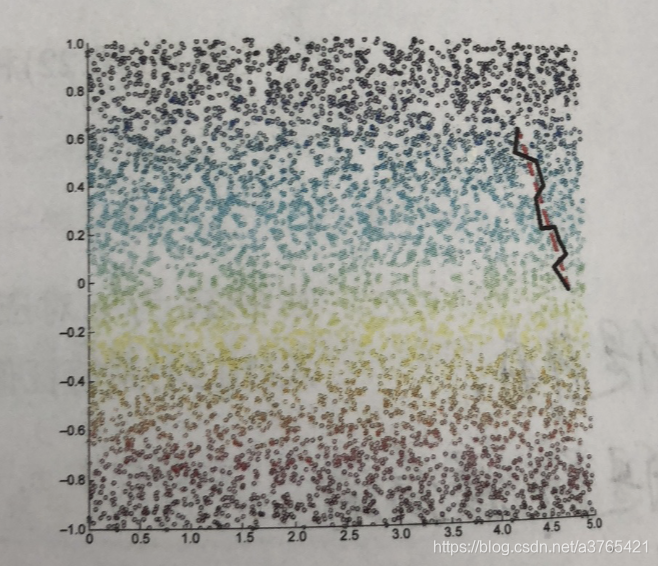
这是在二维中的表现，额，先不在意这个，我们来看看我们应该关注的东西：  什么是近邻距离？

（上图中的红线是我们在S曲面中到达另一样本的测底线距离，）

而近邻距离就是我们找到我们的近邻，然后由近邻找 近邻的近邻，这样一步步下去，最终到达目的地。

当然了，为了路径最短，我们还要想法子。（图算法-最短路径）

 

 

等度量嵌入 的直观：

 

距离近似的方式：高维时两样本之间的距离在降维之后不变。

Isomap算法：

1.遍历每一个样本，找出每一个样本的近邻（类似于K近邻法来找，或者限定某个距离范围内的样本都是其近邻也许）

然后把该样本的近邻样本连接前来/

2.用图算法，计算出所有样本间的距离，形成距离矩阵M，然后利用降维前后样本间距离不变 这样思想的 MDS 算法，得到降维的结果。

 

局部线性嵌入 的直观：

距离近似的核心思想：降维前后，空间中两样本之间的线性关系是不变的，即，线性关系中样本间的Wi是固定的。

LLE 算法：

1.遍历所有的样本，确定他们各自的近邻，并在原本的高维空间中 ，计算得到所有样本与它们近邻样本之间线性关系的Wi，

2. 利用降维后样本间的线性关系是不变的，在低维中空间中列出某个求Z（降维后的向量）的式子，

对该式子推演后会得到一个矩阵M，把M进行特征值分解得到的最小的d个特征值对应的特征向量就是我们求得的解了。

 

 

ok，

 

 

 

88