AcWing 记忆化搜索——901. 滑雪

原题链接：

901. 滑雪 - AcWing题库

题解：

记忆化搜索的实质：通过存储已经遍历过的状态信息，从而避免对同一状态重复遍历的 搜索算法

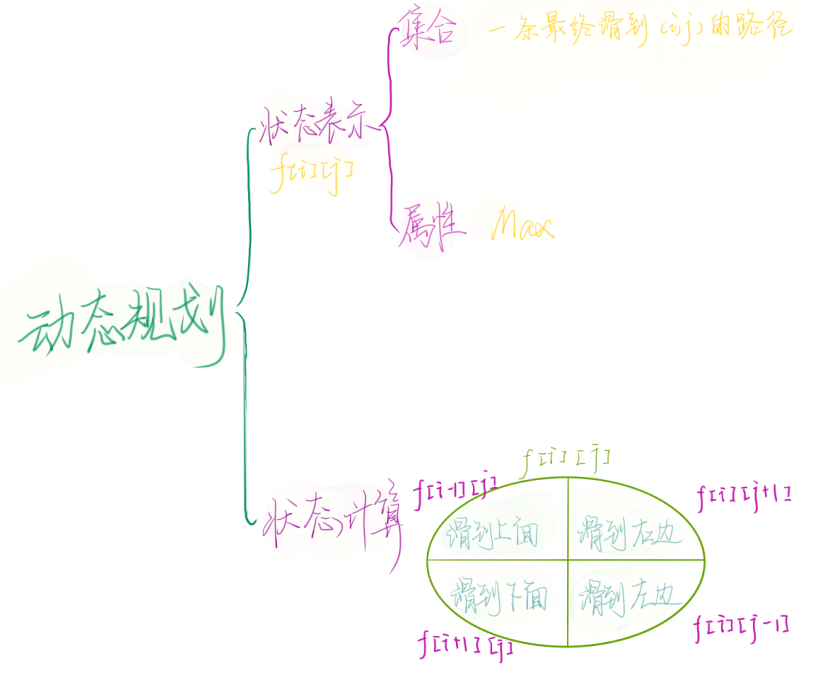
代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 310;
int h[N][N], f[N][N];
int r, c, res;
int t1[] = { -1, 0, 1, 0 }, t2[] = { 0, -1, 0, 1 };

int dp(int x, int y) {
	int& v = f[x][y];
	if (v != -1) return v;//若已经被搜索过，则直接返回记忆值即可
	v = 1;//初始化最小值为1，若为-1会造成错误
	for (int i = 0;i < 4;i++) {
		int a = x + t1[i], b = y + t2[i];
		if (a >= 1 && a <= r && b >= 1 && b <= c && h[x][y]>h[a][b]) v = max(v, dp(a, b) + 1);
	}
	return v;
}

int main() {
	cin >> r >> c;
	for (int i = 1;i <= r;i++)
		for (int j = 1;j <= c;j++) cin >> h[i][j];
	memset(f, -1, sizeof(f));
	for (int i = 1;i <= r;i++)
		for (int j = 1;j <= c;j++)
			res = max(res, dp(i, j));
	cout << res;
}