【数据结构】Stack栈（保姆级+模拟+STL方法函数+小练习）

栈的定义

栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

类比从箱子中拿书，我们得要一本一本地从箱子中拿出来，每次拿的都是最上面的一本。而在放书的时候，我们先放的书会放在箱子的最下面。这就是一个栈，后进先出，意味着后放进去的东西，可以更先拿出来。

图解

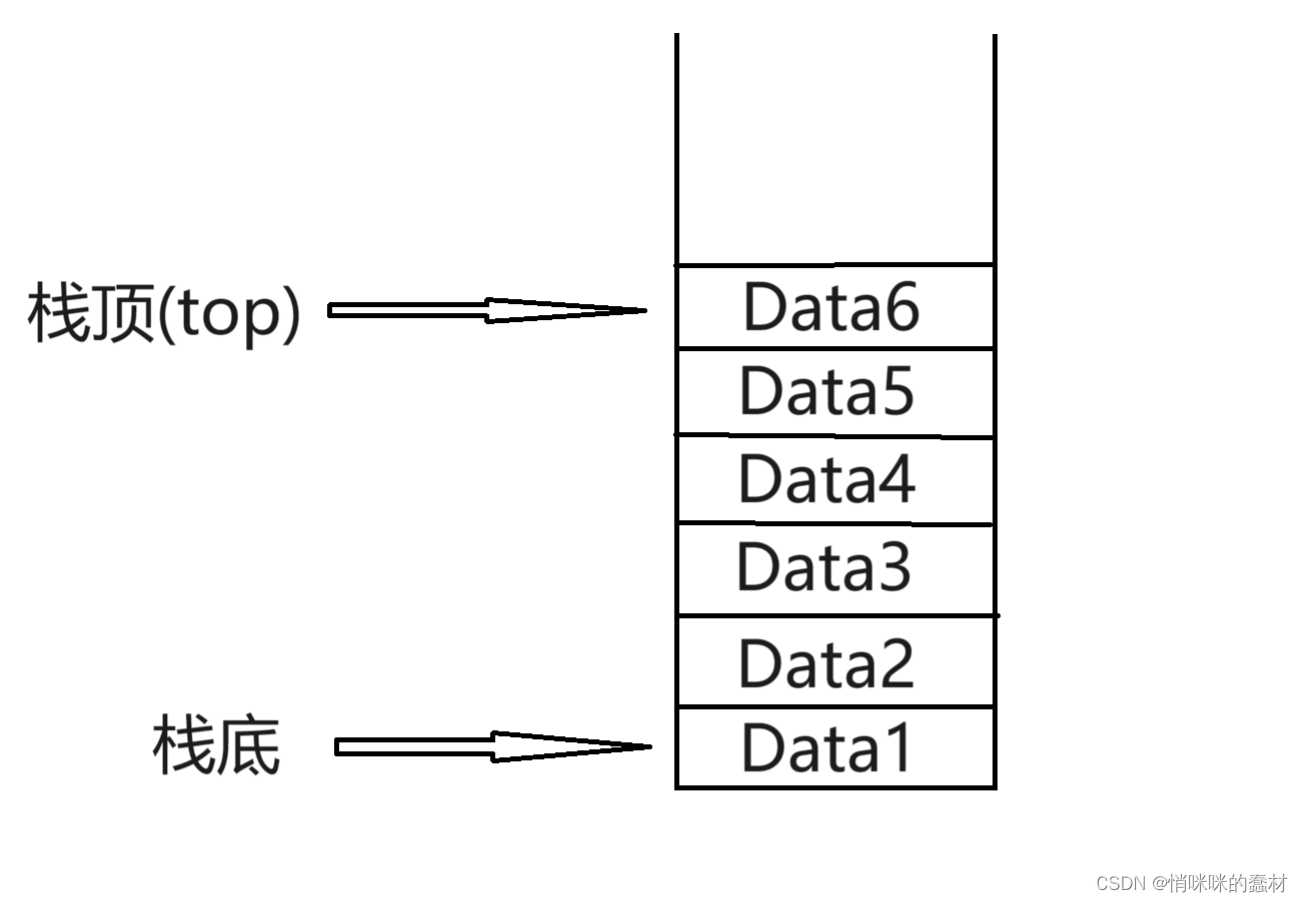
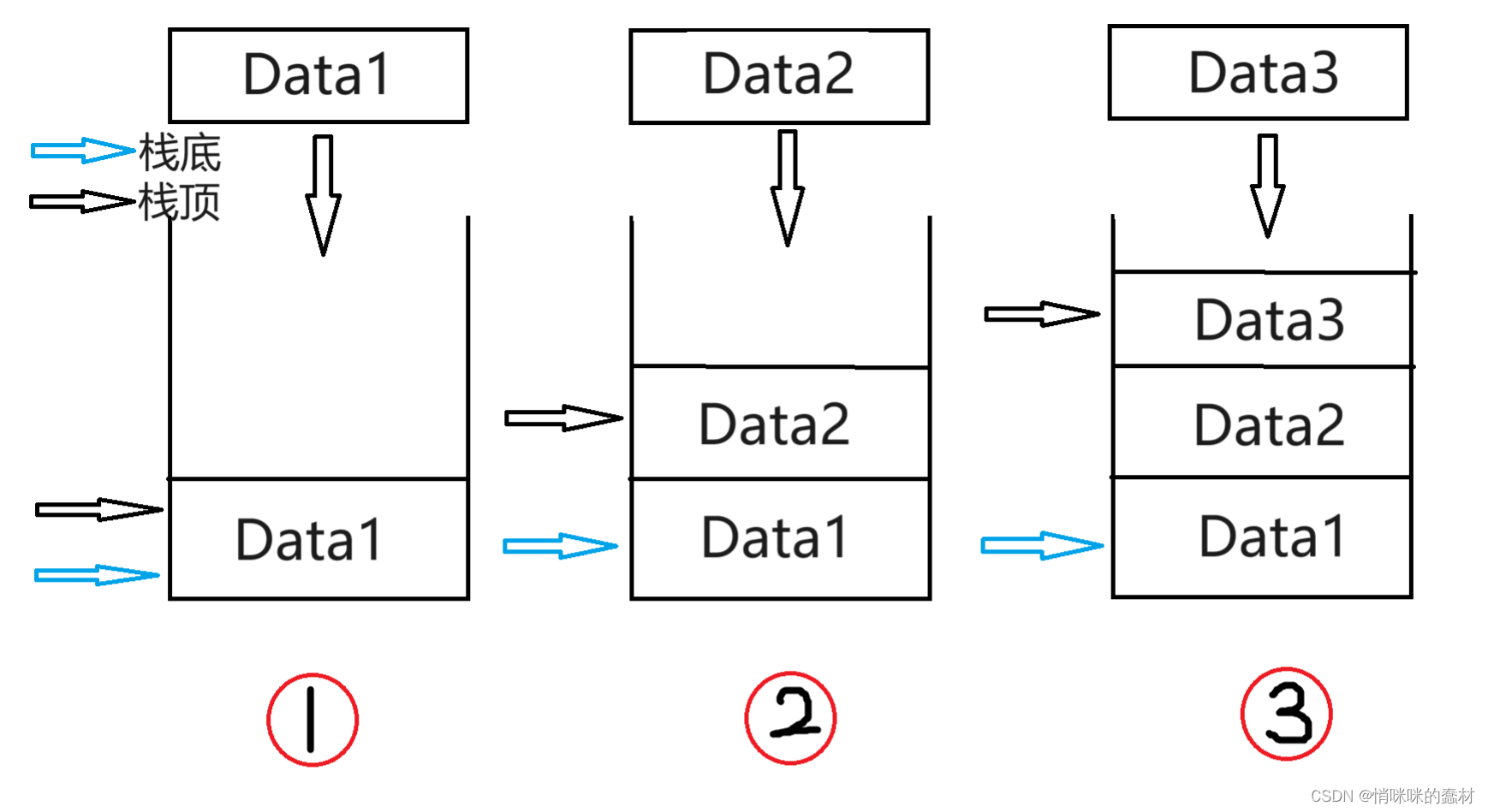
栈的操作

数组模拟

//准备代码
#define Size 4
int Stack[Size];
int StackTop = -1;

1.初始化栈

观察栈，不难发现，栈顶一直在移动，因此需要一个指针StackTop表示栈顶。当StackTop=-1时，意味着栈为空。

void init() { StackTop = -1; cout << "栈被清空" << endl; }

2.入栈

入栈过程中，先入栈，而后更新栈顶，即StackTop++。当栈满时，无法入栈。

void push(int data)
{
	if (StackTop == Size - 1) cout << "栈满，入栈失败" << endl;
	else {
		Stack[++StackTop] = data;
		cout << data << "入栈" << endl;
	}
}
//栈不空时，StackTop其实为数组的下标，因此StackTop最大为Size-1，此时即栈满

3.出栈 (弹出)

出栈过程中，先出栈，而后更新栈顶，即StackTop--。当栈空时，无法出栈。

void pop()
{ 
	if (StackTop == -1) cout << "栈空，弹出失败" << endl;
	else cout << Stack[StackTop--] << "被弹出" << endl;
}

4.获取栈顶元素

不难发现，数据从Stack[0]开始存储，StackTop其实为数据对应位置的下标，因此获取栈顶元素只需要输出Stack[StackTop]

int top(){ return Stack[StackTop];}

5.判断栈是否为空

我们规定栈空为真，因此只需要判断StackTop是否等于-1

bool empty(){ return StackTop == -1;}//栈空返回真

6.得到栈内元素个数

int size() { return StackTop + 1; }

7.可能存在的疑惑？

Q:为什么StackTop以-1为初始，而不是-2或者别的数字?

A:因为是先入栈再StackTop++；因此-1为初始方便了StackTop从0开始有效，从而可以作为数据在数组中的下标。

Q:为什么清空栈只需要让StackTop=-1，而不需要清除数组中的元素？

A:在入栈的时候，是会先更新数据的，因此旧数据如何并不影响。并且栈顶就是任何操作的数据范围上限，不会涉及任何旧数据。在弹出的过程中，也只需要StackTop--，并不需要清除栈顶的元素。

Q:为什么栈空返回真？

A:因为STL中有empty函数，其定义就是空为真，可见下文。

8.完整代码以及测试

#include<iostream>
using namespace std;
#define Size 4
int Stack[Size];
int StackTop = -1;

void init() { StackTop = -1; cout << "栈被清空" << endl; }
void push(int data)
{
	if (StackTop == Size - 1) cout << "栈满，入栈失败" << endl;
	else {
		Stack[++StackTop] = data;
		cout << data << "入栈" << endl;
	}
}
void pop()
{ 
	if (StackTop == -1) cout << "栈空，弹出失败" << endl;
	else cout << Stack[StackTop--] << "被弹出" << endl;
}
int top(){ return Stack[StackTop];}
bool empty(){ return StackTop == -1;}//栈空返回真
int size() { return StackTop + 1; }
int main()
{
	init();
	push(1);
	push(2);
	push(3);
	push(4);
	push(5);
	pop();
	cout <<"栈顶元素为：" << top() << endl;
	cout << "栈大小为：" << size() << endl;
	pop();
	pop();
	init();
	cout << empty() << endl;
	push(10);
	cout <<"栈大小为" << size() << endl;
	return 0;
}

STL中Stack方法函数

创一个栈

#include<stack>//头文件不要忘记
stack<int> a;

方法函数

a.push(data);//入栈data
a.pop();//弹出栈顶元素
a.size();//获取栈的元素个数
a.empty();//判空
a.top();//获取栈顶元素

*STL没有栈清空的函数

附代码加深理解

#include<iostream>
#include<stack>
using namespace std;

int main()
{
	stack<int> a;
	a.push(1);
	a.push(2);
	cout << a.size() << endl;
	a.pop();
	cout << a.top() << endl;
	a.pop();
	if (a.empty()) cout << "栈空" << endl;
	else cout << "栈不空" << endl;
	return 0;
}

小练习

1.洛谷P1427小鱼的数字游戏

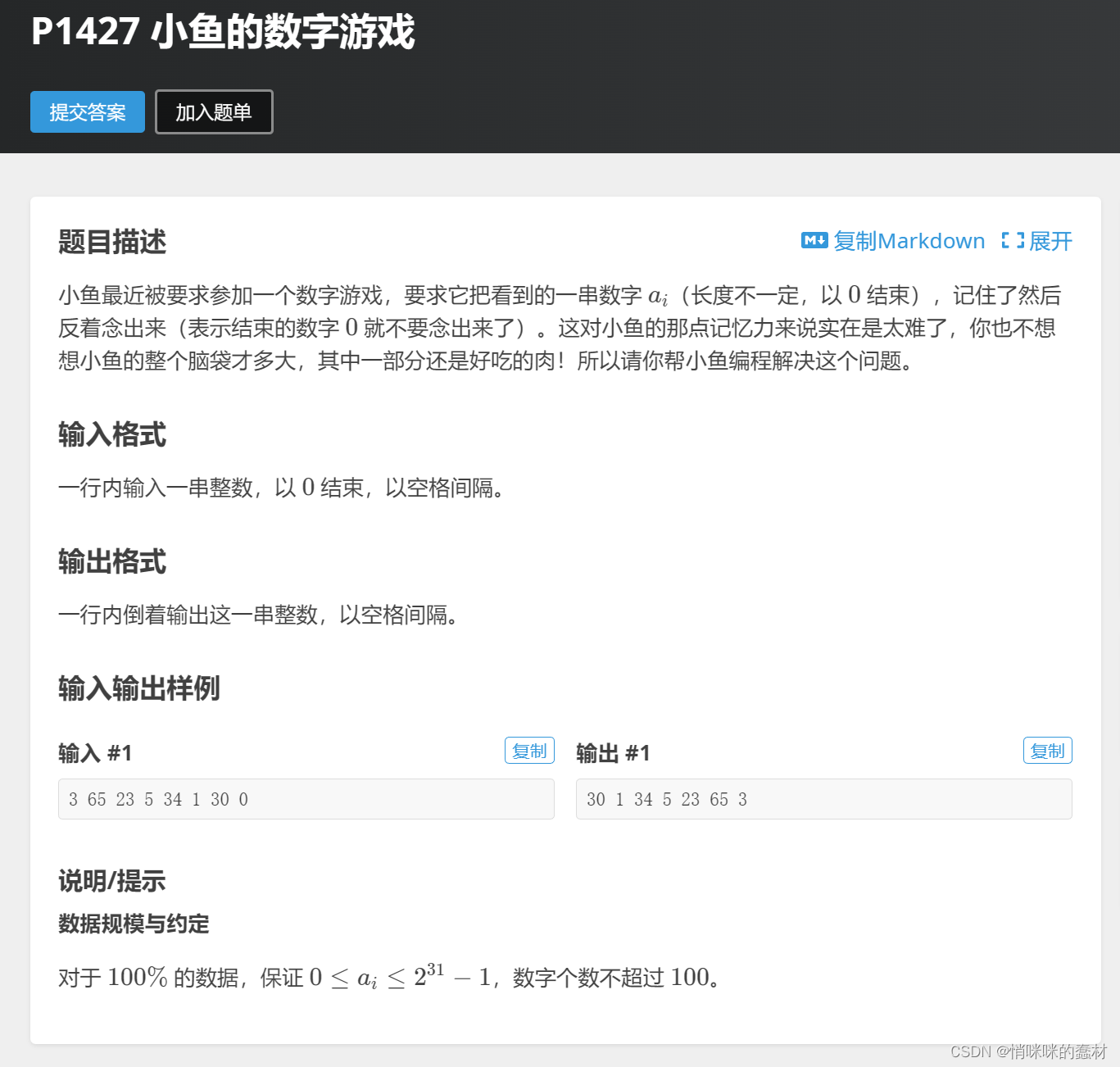
只需要依次入栈再依次出栈即可

#include<iostream>
#include<stack>
using namespace std;

int main()
{
	stack<int> a;
	int b;
	while (cin>>b&&b!=0)
	{
		a.push(b);
	}
	while (!a.empty())
	{
		cout << a.top() << " ";//先用后弹出
		a.pop();
	}
	return 0;
}

2.洛谷P1739表达式括号匹配

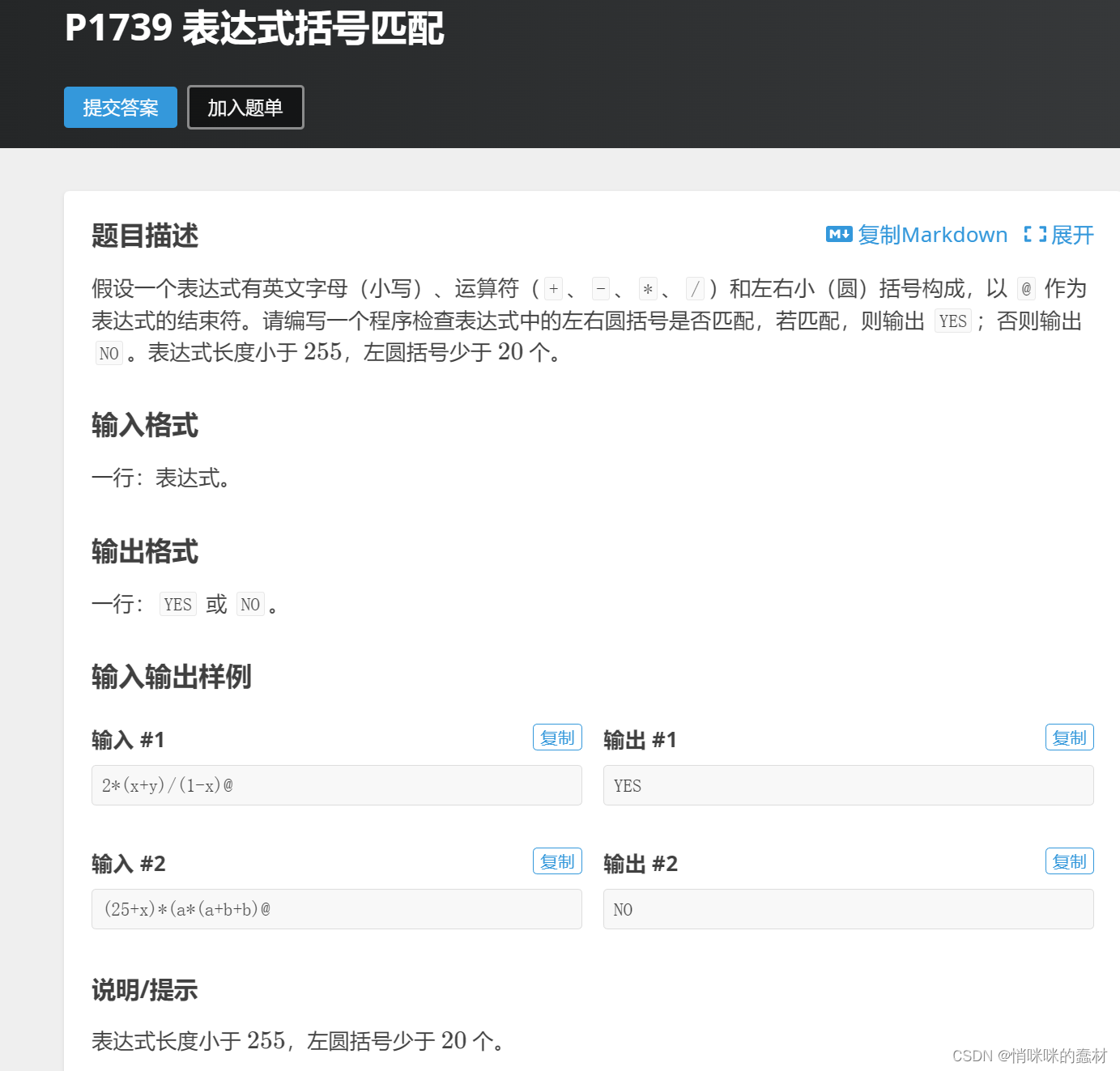
当遇到(时，(入栈，遇到)时，(出栈，以和)对应匹配。在遇到)前需要先判断一下栈是否空，如果为空，则无匹对的(，直接输出NO。最后，判断栈是否为空，也就是是否()全部匹配好，如若空，则YES，否则NO

#include<iostream>
#include<stack>
using namespace std;

int main()
{
	stack<char> a;
	char b;
	while (cin >> b && b != '@')
	{
		if (b == '(') a.push(b);
		if (b == ')')
		{
			if (a.empty())
			{
				cout << "NO";
				return 0;
			}
			else a.pop();
		}
	}
	if (a.empty()) cout << "YES";
	else cout << "NO";
}

3.力扣844比较含退格的字符串

模拟即可

class Solution {
public:
    bool backspaceCompare(string s, string t) {
    stack<char> a, b;
    solve(s,a);
    solve(t,b);
    if (a.size() != b.size()) return false;
    else {
        int sum = a.size();
        for (int i = 0; i < sum; i++)
        {
            if (a.top() != b.top()) return false;
            else 
            {
                a.pop();
                b.pop();
            }
        }
    }
    if ((!a.empty()) || (!b.empty())) return false;
    else return true;
    }
    void solve(string x,stack<char>& m)
    {
         for (int i = 0; i < x.size(); i++)
    {
        if (x[i] == '#')
        {
            if(m.empty()) continue;
            m.pop();
        }
        else m.push(x[i]);
    }
    }
};