算法设计

方法	试用情况
分治法	各子问题独立
动态规划	各子问题重叠
贪心

1.分治

分治算法能解决问题的特征:
–问题规模缩小到一定的程度可以容易地解决
–问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质
–利用该问题分解出的子问题的解可以合并为该问题的解
–该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题

解题步骤：
– 划分阶段的时间复杂性
• 划分问题为a个子问题。
• 每个子问题大小为n/b。
• 划分时间可直接得到=D(n)
– 递归求解阶段的时间复杂性
• 递归调用
• 求解时间= aT(n/b)
– 合并阶段的时间复杂性
• 时间可以直接得到=C(n)

复杂度：
• T(n)=(1) if n<c
• T(n)=aT(n/b)+D(n)+C(n) if nc

2.动态规划

• 分治技术的问题
– 子问题是相互独立的
– 如果子问题不是相互独立的，分治方法将重复计算公共子问题，效率很低

• 动态规划算法特点
– 把原始问题划分成一系列子问题
– 求解每个子问题仅一次，并将其结果保存在一个表中，以后用到时直接存取，不重复计
算，节省计算时间
– 自底向上地计算

使用Dynamic Programming的条件：
– Optimal substructure（优化子结构）
• 一个问题的优化解包含了子问题的优化解
– Subteties（重叠子问题）
• 在问题的求解过程中，很多子问题的解将被多次使用

例1：
最长公共子序列LCS

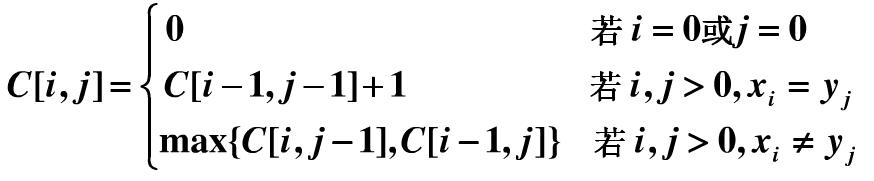
例2：
矩阵链乘
优化子结构：
A1n=A1kAk+1n，则在A1n的优化顺序中，对应于子问题A1k的解必须是A1-k的优化解，对应于子问题Ak+1n的解必须是Ak+1n的优化解
m[i, i] = 计算Ai  i 的最小乘法数= 0
m[i, j] = m[i, k] + m[k+1, j] + pi-1pkpj
其中, pi-1pkpj是计算AikAk+1j所需乘法数,
Ai k和Ak+1  j分别是pi-1pk和pkpj矩阵.



时间复杂度（n3）空间（n2)

3.贪心

贪心选择性：一个全局最优解可以通过局部最优得到。
即存在一个最优解是以贪心选择开始的。

优化子结构：一个最优解包括期子问题的最优解。
即一个n的最优解分解成第一步的贪心选择，和n-1的子问题，这个n-1的子问题也是最优的。

最后要说明，第一步的贪心选择和n-1的子问题可以合并成一个全局最优解。