输入一个正整数，判断是否为素数

要判断一个数是否为素数，我们需要理解素数的定义：一个大于1的自然数，如果除了1和它自身外，不能被其他自然数整除，那么这个数就是素数。

基于这个定义，最直接的思路是从2开始，逐个检查每个数是否能整除目标数。如果找到任何一个能整除的数，就说明目标数不是素数；如果一直检查到目标数减1都没有找到能整除的数，就说明目标数是素数。

但这种基础方法效率较低，我们可以进行优化。观察发现，如果目标数n有因子，那么因子一定是成对出现的。比如n=12，因子对有(2,6)、(3,4)。在每一对因子中，较小的那个一定不会超过√n。因此我们只需要引入数学库用sqrt函数检查到√n即可，这大大减少了循环次数，提高了效率

另外，除了2以外的所有偶数都不是素数，所以我们可以先排除偶数，然后在循环中只检查奇数，这样又能减少一半的检查次数

#include <stdio.h>
#include<math.h>
int prime(int i)//定义函数prime,返回值是标志flag取值0或1
{
	int flag;
	if (i % 2 != 0 || i == 2)//先判断是不是奇数
	{
		flag = 1;
		for (int j = 2; j < sqrt(i); j++)//设置除数范围
		{
			if (i % j == 0)
			{
				flag = 0;
			}
		}
		return flag;
	}
	
}
int main()
{
	printf("请输入一个整数");//提示用户输入
	int a, flag;
	scanf("%d", &a);
	flag=prime(a);
	if (flag == 1)//根据函数返回值0，1判读是否为素数
	{
		printf("%d是素数",a);
	}
	else {
		printf("%d不是素数", a);
	}
	
	return 0;
}

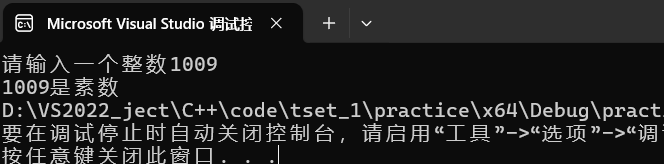
在VS2022中运行截图