AcWing 51. 数字排列（DFS（有重复排列+无重复排列））

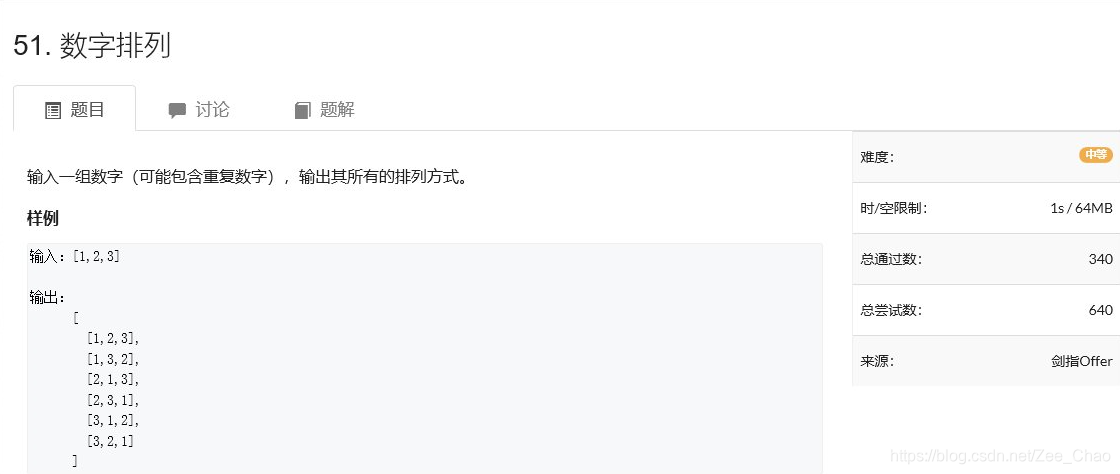
OJ上这道题的描述并不清晰。实际上，它的要求是输出所有“不重复的排列方式”。

1.next_permutation()（无重复排列）

要解决数组无重复排列的问题，那么这个方法是再合适不过的了。在使用这个函数前注意要引入<algorithm>头文件并且为了保证可以枚举所有情况要实现对数组进行“由小到大”的排序。

具体代码如下：

class Solution {
public:
    vector<vector<int>> permutation(vector<int>& nums) {
        vector<vector<int>> ans;
        sort(nums.begin(), nums.end());
        do{
            ans.push_back(nums);
        }while(next_permutation(nums.begin(), nums.end()));
        return ans;
    }
};

2.DFS（有重复排列（交换+循环遍历））

这里提供两种思路。

首先是交换。可以将整个数组分成两部分：第一个元素和其他元素。求全排列的过程可以看成两个子过程，一个是确定首元素，另一个是确定剩余元素的全排列（其中，如果确定的首元素不是nums[0]，则交换该元素和nums[0]）。显然，剩余元素全排列的求解就是递归执行以上过程。

具体代码如下：

class Solution {
public:
    void dfs(vector<vector<int>> &ans, vector<int> nums, int cur){
        if(cur == nums.size()) {
            ans.push_back(nums);
            return;
        }
        for(int i = cur; i < nums.size(); i++){
            swap(nums[cur], nums[i]); //通过交换方式将首元素放置到起始位置
            dfs(ans, nums, cur + 1);
        }
    }
    
    vector<vector<int>> permutation(vector<int>& nums) {
        vector<vector<int>> ans;
        dfs(ans, nums, 0);
        return ans;
    }
};

第二种思路就是循环遍历。利用标记数组记录每一个原数组中的元素是否被访问到，根据递归加循环遍历的次序依次将元素插入中间结果数组中。当递归到达出口时将中间结果存入最终结果当中。

具体代码如下：

class Solution {
public:
    vector<vector<int>> ans; //存放最终结果
    vector<int> temp; //存放中间结果
    vector<int> mark; //标记数组

    void dfs(vector<int> &nums, int cur){
        if(cur == nums.size()) {
            ans.push_back(temp);
            return;
        }
        for(int i = 0; i < nums.size(); i++){
            if(!mark[i]){
                mark[i] = 1;
                temp[i] = nums[cur];
                dfs(nums, cur + 1);
                mark[i] = 0;
            }
        }
    }
    
    vector<vector<int>> permutation(vector<int>& nums) {
        temp.resize(nums.size());
        mark = vector<int> (nums.size(), 0);
        dfs(nums, 0);
        return ans;
    }
};

需要特别说明的是：虽然两份代码中的函数参数完全一致，但是其中cur的含义并不相同！第一份代码中的cur指的是确定好结果数组首元素后剩余子数组的起始位置。而第二份代码中的cur则指的是将要判断是否要插入到结果数组中的元素在原数组中的位置。

如果从时空复杂度的角度上来看，后者的复杂度无论在时间还是空间上均要高于前者。不过，后者的方法比前者更容易扩展到无重复排列的情况！

3.DFS（无重复排列）

核心思路与有重复排列的思想一致，需要额外考虑就是如何去重。可以考虑将每一次的结果进行记录，如果后面有遇到已经保存过的结果则直接跳过（由于思路比较简单且时空复杂度较高，这里不再提供代码）。或者还可以根据DFS具有回溯的性质，对已经使用的原数组的元素进行标记。这里提供两种不同的标记方法，其中一种使用了规模与原数组相同的标记数组，另一种则采用二进制的方式来记录每个元素的标记情况。这两种方法都是从有重复排列的第二种思想的代码上扩展得来的。

该方法大致的思路是：首先对原数组进行排序操作从而让所有相同的元素相邻；在原算法的基础上新增一个变量start用来记录当前递归中循环选择元素的起始位置。（对于有重复排列而言，start是恒为0的。实际上这也正是会产生重复排列的原因）；如果说当前元素与下一个要判断是否加入到结果中的元素不同，则不做任何修改，仍然按照原来的有重复算法执行。但是如果当前元素与下一个要判断是否加入到结果中的元素相同，则下一层递归的遍历就要从当前递归所加入的元素在原数组中的位置的下一个位置（也就是i+1）开始。

具体代码如下：

class Solution {
public:
    vector<vector<int>> ans; //存放最终结果
    vector<int> temp; //存放中间结果
    vector<int> mark; //标记数组

    void dfs(vector<int> &nums, int cur, int start){
        if(cur == nums.size()) {
            ans.push_back(temp);
            return;
        }
        for(int i = start; i < nums.size(); i++){
            if(!mark[i]){
                mark[i] = 1;
                temp[i] = nums[cur];
                if(cur + 1 < nums.size() && nums[cur] != nums[cur + 1])
                    dfs(nums, cur + 1, 0);
                else
                    dfs(nums, cur + 1, i + 1);
                mark[i] = 0;
            }
        }
    }
    
    vector<vector<int>> permutation(vector<int>& nums) {
        temp.resize(nums.size());
        mark = vector<int> (nums.size(), 0);
        sort(nums.begin(), nums.end());
        dfs(nums, 0, 0);
        return ans;
    }
};

另外，还可以用二进制的方式来存放原数组中元素的访问信息。二进制由低到高分别记录原数组从头到尾的元素的访问情况。1代表已访问，0代表未访问。

具体代码如下：

class Solution {
public:
    vector<vector<int>> ans; //存放最终结果
    vector<int> temp; //存放中间结果
    
    void dfs(vector<int> &nums, int cur, int start, int state){
        if(cur == nums.size()) {
            ans.push_back(temp);
            return;
        }
        for(int i = start; i < nums.size(); i++){
            if(!(state >> i & 1)){
                temp[i] = nums[cur];
                if(cur + 1 < nums.size() && nums[cur] != nums[cur + 1])
                    dfs(nums, cur + 1, 0, state + (1 << i));
                else
                    dfs(nums, cur + 1, i + 1, state + (1 << i));
            }
        }
    }
    
    vector<vector<int>> permutation(vector<int>& nums) {
        temp.resize(nums.size());
        sort(nums.begin(), nums.end());
        dfs(nums, 0, 0, 0);
        return ans;
    }
};