构造最小生成树Prim算法(C语言)

提示：通过用Prim算法构造最小生成树解决连接偏远地区村落间道路最少花费问题

目录

前言

输入格式:

输出格式: 

一、什么是Prim算法

二、如何使用Prim算法解决问题

1.分析问题

2.完整代码实现

二、总结

---

前言

某地对偏远地区实行“村村通”工程，目标是使整个地区任何两个村落间都可以实现快速交通（但不一定有直接的快速道路相连，只要互相间接通过快速路可达即可）。现得到拟修建道路的费用，现请你编写程序，计算出全地区畅通需要的最低成本。

输入格式:

输入的第一行给出村庄数目N (1≤N≤20)和拟修建的道路数M

接下来的M行对应修建每条村庄间道路的成本，每行给出3个正整数，分别是两个村庄的编号（从1编号到N），此两村庄间道路的成本。

输出格式: 

输出需修建的道路，按prim算法从编号1开始得到的顺序，输出每条路，每行输出一条道路，形式如：道路1编号,道路2编号,费用。(编号小的放前面，编号大的放后面，逗号为英文状态下的逗号)

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、什么是Prim算法

Prim算法采用“子树延伸”原理。从单节点树开始，沿着此节点最短边一个一个地向外生长，在构造过程中不会产生回路，直至将所有节点连起来，得到一颗生长树。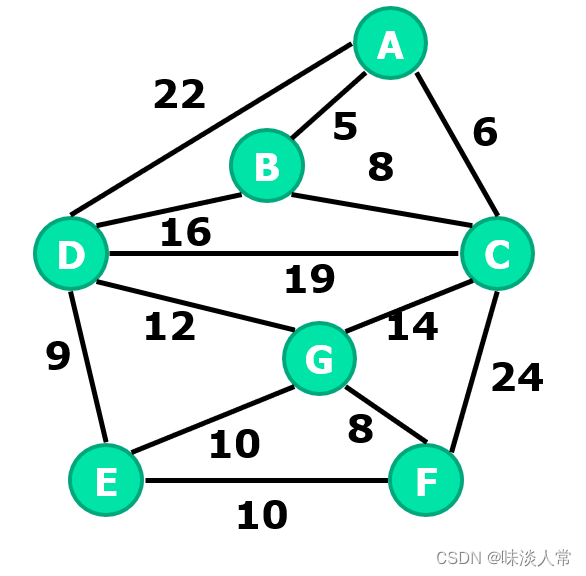   

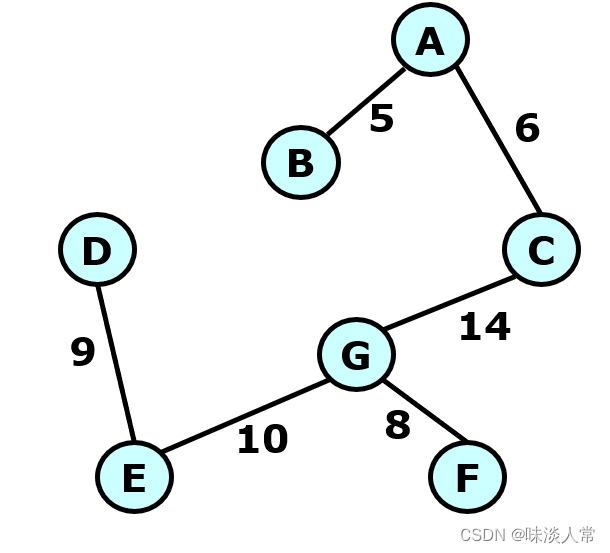
 如上左图—>右图的过程

二、如何使用Prim算法解决问题

1.分析问题

根据题目有

假设输入为

4 6

1 2 1

1 3 4

1 4 1

2 3 3

2 4 2

3 4 5

则输出应是

1,2,1

1,4,1

2,3,3

具体分析如下

①画出无向带权图

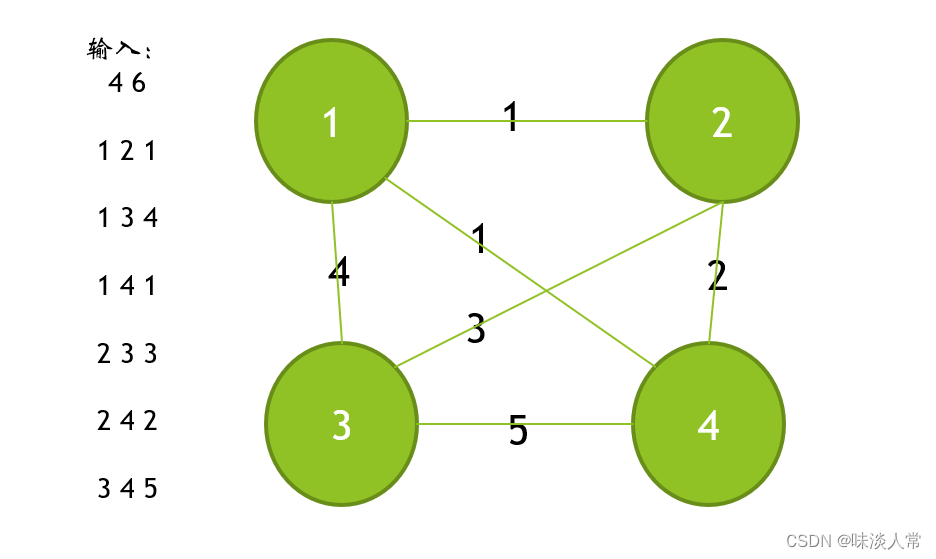
②用邻接矩阵构造此图

代码如下（示例）：

int L[25][25] = { 0 };//将邻接矩阵全部置零
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			if (i != j)
				L[i][j] = 1000;       //保留邻接矩阵中自环的值为零，其余边的花费为MAX=1000，一个相对极大的数
		}
	}
	for (int i = 0; i < M; i++)    //将两点间有直接相连的边权值存入，得到一个能表示一个节点与其它所有节点之间的花费如 ∞（MAX），0等
	{
		scanf("%d%d%d", &p, &q, &w);//构造邻接矩阵，将两点间有直接关系的边的花费存入

		L[p - 1][q - 1] = w;    //邻接矩阵从L[0][0]开始存储，但节点名从1开始，所以为了方便起见将节点名减一则刚好匹配
		L[q - 1][p - 1] = w;    //因为存储的是无向带权图，故在邻接矩阵中对称位置权值相等
	}

③设置边节点类型，用于存储

代码如下（示例）

typedef  struct  edge_node
{
	int  incr_vert, vertex;   //前者为生长点，后者为非生长点
	int  cost;  	//边的花费
}edge;   //边节点的类型结构

④构造初始待选边表（以0作为初始生长点）

开始时选择顶点（0）作为初始生长点，对其余每个非生长点v（共n-1个），将边（0，v)加入待选边表，如果边（0，v）不存在，则认为权值为∞，即上文所说的MAX（1000）。

int v, i, j, k;          
	edge  t, wait[100]; //存储待选边表的数组
	for (v = 0; v < n - 1; v++) 	  //以顶点0作为初始生长点建立初始待选边表
	{
		wait[v].incr_vert = 0;           //生长点
		wait[v].vertex = v + 1;   	  //非生长点
		wait[v].cost = L[0][v + 1];
	}

 ⑤循环n-2遍，非生长点个数从n-1变成1

先选择最短待选边

k = i;   //找最短的待选边（简单选择排序）
		for (j = i + 1; j < n - 1; j++)
		{
			if (wait[j].cost < wait[k].cost)k = j;
		}

再修改待选边表

for (i = 0; i < n - 2; i++) 
	{
		k = i;   //找最短的待选边（简单选择排序）
		for (j = i + 1; j < n - 1; j++)
		{
			if (wait[j].cost < wait[k].cost)k = j;
		}
		t = wait[k];  
		wait[k] = wait[i];  
		wait[i] = t;	//得到一条树边，换到数组前部
		v = wait[i].vertex; 		                 //v作为新的生长点
		for (j = i + 1; j < n - 1; j++) 		                 //修改待选边表 
			if (wait[j].cost > L[v][wait[j].vertex]) {
				wait[j].cost = L[v][wait[j].vertex];
				wait[j].incr_vert = v;
			}
	}

2.完整代码实现

代码如下（示例）：

#define _CRT_SECURE_NO_DEPRECATE
#include<stdio.h>
typedef  struct  edge_node
{
	int  incr_vert, vertex;   //前者为生长点，后者为非生长点
	int  cost;  	//边的花费
}edge;   //边节点的类型结构

void  Prim(int M, int n)
{
	int p, q, w;
	int L[25][25] = { 0 };//将邻接矩阵全部置零
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			if (i != j)
				L[i][j] = 1000;       //保留邻接矩阵中自环的值为零，其余边的花费为MAX=1000，一个相对极大的数
		}
	}
	for (int i = 0; i < M; i++)    //将两点间有直接相连的边权值存入，得到一个能表示一个节点与其它所有节点之间的花费如 ∞（MAX），0等
	{
		scanf("%d%d%d", &p, &q, &w);//构造邻接矩阵，将两点间有直接关系的边的花费存入

		L[p - 1][q - 1] = w;    //邻接矩阵从L[0][0]开始存储，但节点名从1开始，所以为了方便起见将节点名减一则刚好匹配
		L[q - 1][p - 1] = w;    //因为存储的是无向带权图，故在邻接矩阵中对称位置权值相等
	}
	for (int i = 0; i < n; i++)//输出该邻接矩阵
	{
		for (int j = 0; j < n; j++)
		{
			printf("%d ", L[i][j]);
		}
		printf("\n");
	}
	int v, i, j, k;          
	edge  t, wait[100]; //存储待选边表的数组
	for (v = 0; v < n - 1; v++) 	  //以顶点0作为初始生长点建立初始待选边表
	{
		wait[v].incr_vert = 0;           //生长点
		wait[v].vertex = v + 1;   	  //非生长点
		wait[v].cost = L[0][v + 1];
	}
	for (i = 0; i < n - 2; i++) 
	{
		k = i;   //找最短的待选边（简单选择排序）
		for (j = i + 1; j < n - 1; j++)
		{
			if (wait[j].cost < wait[k].cost)k = j;
		}
		t = wait[k];  
		wait[k] = wait[i];  
		wait[i] = t;	//得到一条树边，换到数组前部
		v = wait[i].vertex; 		                 //v作为新的生长点
		for (j = i + 1; j < n - 1; j++) 		                 //修改待选边表 
			if (wait[j].cost > L[v][wait[j].vertex]) {
				wait[j].cost = L[v][wait[j].vertex];
				wait[j].incr_vert = v;
			}
	}
	for (i = 0; i < n - 1; i++)
	{
		printf("%d,%d,%d\n", (wait[i].incr_vert + 1)<(wait[i].vertex + 1)? (wait[i].incr_vert + 1): (wait[i].vertex + 1), (wait[i].incr_vert + 1) > (wait[i].vertex + 1) ? (wait[i].incr_vert + 1) : (wait[i].vertex + 1), wait[i].cost);
//此处用了三目运算符使得较小编号先输出

	}
}


int main()
{
	int N, M;
	scanf("%d%d", &N,&M);//N为村庄数，M为计划修建道路数
	
	Prim(M, N);

	return 0;

}

---

二、总结

Prim算法思想是选最短边，且只带待选边表中选最短边。

Prim算法不需要判断是否产生回路。

时间复杂度是O（n^2）,耗时取决于顶点数n。