(动态规划)最长公共子序列

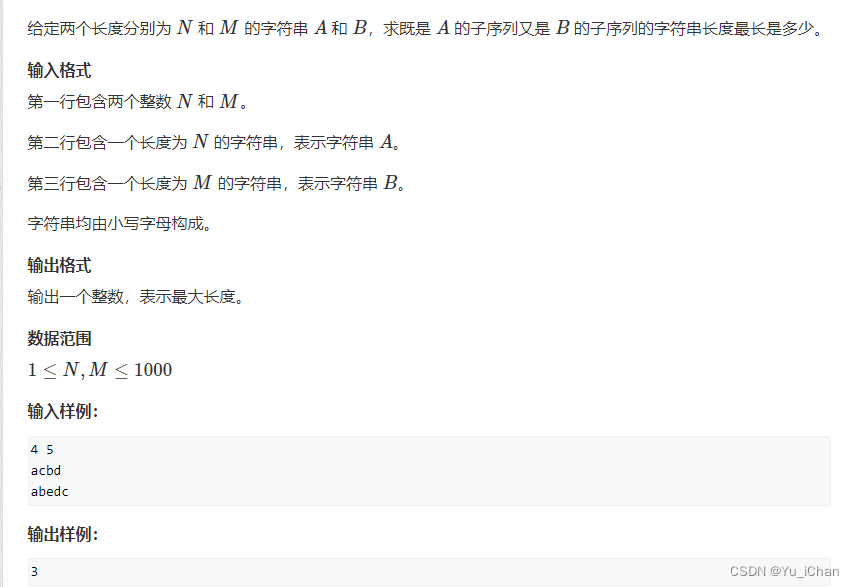
 首先必须得是a和b的公共子序列

我们用f[i][j]表示a中1~i与b中1~j的公共子序列的集合，题目要求最长公共子序列所以集合的属性就是max

想想如何划分f[i][j]动态规划中一般状态计算，我们都是从它的前一个状态来计算

所以f[i][j]这个集合我们可以粗略的分成四种

用0表示不含a[i],b[j]

用1表示含有a[i],b[j]

所以分为00，01，10，11

首先是00这种情况实际就是f[i][j]=f[i-1][j-1]

11要满足条件a[i]==b[j]才能成立  也就是如果满足条件的话 f[i][j]=f[i-1][j-1]+1

再来就是01以及10这个了

01代表不含有a[i],含有b[j]  有同学肯定就会想它是不是直接就是f[i-1][j]，答案是否定的

可以看一看对于f的定义的表示 所以f[i-1][j]中有包含b[j]的也有 不包含b[j]的一类

如果有包含b[j]的一类的话那么是不是代表着00这种情况已经包含在了01和10中了

因为我们求的是最大值，所以只要包含了01这种情况就可以,重复是没有关系的

好比求a,b,c中最大值  先(a,b)再(b,c）再把他们之中较大的比较

重复求了b相当于但是不影响结果

                                                                                                                                                                                       

#include<iostream>
using namespace std;

const int N=1010;

char a[N],b[N];
int f[N][N];
int n,m;

int main()
{
    cin>>n>>m;
    cin>>a+1>>b+1;
    
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            f[i][j]=max(f[i-1][j],f[i][j-1]);//因为00已经包含在01或10中了所以不需要考虑
            if(a[i]==b[j])f[i][j]=max(f[i][j],f[i-1][j-1]+1);
        }
    cout<<f[n][m];
    
    return 0;
}

                                                                                                                                                                                             

所以我们只用考虑三个集合就可以了取三个集合的最大值中的最大值