走迷宫(bfs)(c++）个人纪录向

最新推荐文章于 2025-12-07 21:20:15 发布

原创最新推荐文章于 2025-12-07 21:20:15 发布 · 97 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#宽度优先 #算法 #c++

本文介绍了如何使用宽度优先搜索（BFS）解决从(1,1)出发的迷宫问题，利用二维数组记录路径，并通过队列进行广度优先遍历。在C++中，通过内置的queue容器实现队列，同时存储行和列坐标。BFS函数逐层查找，考虑上下左右四个方向的相邻点，确保它们存在于迷宫中且未被访问过。" 114233594,6873162,Java BlockingQueue 实现与源码分析,"['Java', '并发编程', '数据结构']

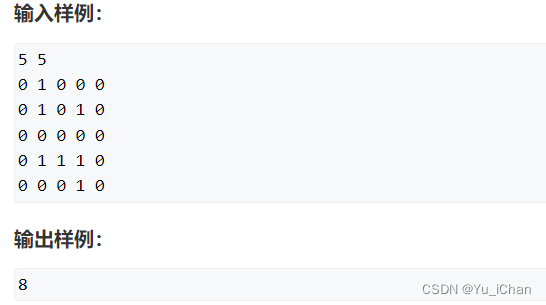
像这样的权值可以看作是1的图，最短路问题就可以用bfs来做,否则的话就得用别的方法做了

这个图我们根据题意就从(1,1)开始赋值而不是从(0,0)开始，虽然从0开始的话也是一样

我们需要定义一个二维数组g[N][N]来存储输入的1和0来记录这条路通不同行。以及一个dis[N][N]数组来记录每个点距离(1,1)的距离，所以我们的dis[n][m]就是答案

同样bfs的话我们就要用到队列了，这里我们可以同c++自带的容器queue，也可以自己手写一个队列，但是注意这里的队列我们是需要存储两个数的pair,因为是二维数组，我们需要存储它的行和列

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;

const int N=110;
int g[N][N],dis[N][N];
typedef pair<int,int> PII;
int n,m;

int main()
{
    memset(dis,-1,sizeof dis);//把距离初始成-1来判断是不是走过了这个点
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            cin>>g[i][j];
    
    cout<<bfs()<<endl;
    return 0;
}

接下来就是我们的bfs函数了

广度优先搜索是一层一层的找的,也就是说我们从一个点去找这个点的相邻的点,那么是不是我们每次都是只能找上下左右四个点呢，前提是这四点确实存在并且没有被找到过。

我们可以定义一个偏移量dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};dx[i]和dy[i]都对应着向上右下左分别移动一格



int bfs()
{
    queue<PII> q;
    dis[1][1]=0;
    q.push({1,1});
    while(q.size())
    {
        auto t=q.front();
        q.pop();
        int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};//偏移量的定义，也就是去寻找上下左右
        for(int i=0;i<4;i++)
        {
            int x=t.first+dx[i];//去找到t这个点的上下左右点
            int y=t.second+dy[i];
            if(x>0&&x<=n&&y>0&&y<=m&&g[x][y]==0&&dis[x][y]==-1)//判断找到点是不是在图的范围内有没有越界，并且g[x][y]是可以通行的也就是其等于0,并且这个点没有被找到过
            {
                dis[x][y]=dis[t.first][t.second]+1;
                q.push({x,y});
            }
        }
    }
    return dis[n][m];
}