pat甲级1151 LCA in a Binary Tree 最近公共祖先

        题目思路：给定先序和中序即可确定一棵树。寻找最近公共祖先 ，俩个点若在同一棵子树下，俩个点的公共祖先是当前子树的根节点，如何寻找最近公共祖先呢？那就要一直递归，直到俩个点第一次不在同一棵子树下，那么上一个子树的根节点就是最近祖先。

        例子如下图。

 

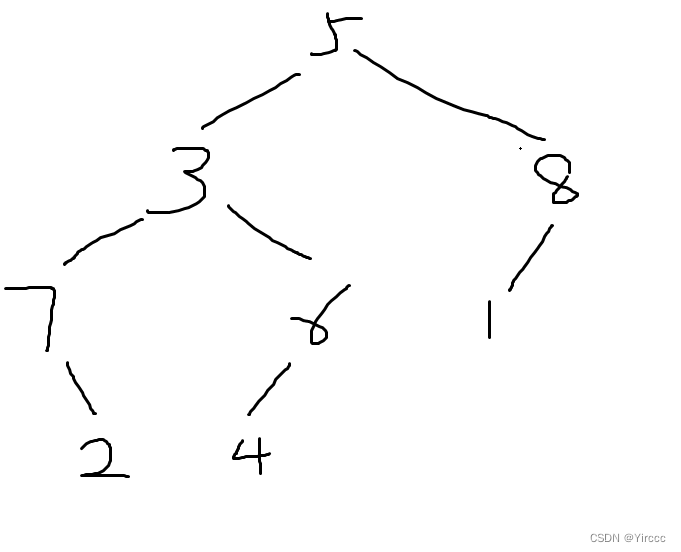
         假设要求2，4的最近公共祖先，那么一开始的祖先肯定是5，然后进入左子树，但是再往下会发现2的祖先是7，4的是6，俩个点第一次不在同一棵子树下，则上一次的公共祖先是3，则答案为3

 dfs函数参数解释：inl是中序的左边界，inr是中序的右边界，preroot是先序当前子树的根节点下标，u和v就是要求的俩个点

部分代码解释：

 dfs(inl , inroot-1 , preroot+1 , u , v) ; //递归进入左子树，在中序中（左根右），左子树的右边界是根节点左边第一个，左子树的左边界不变，在先序中（根左右），左子树的根节点是当前根节点的下标的下一个

 dfs(inroot+1 , inr , preroot+1+inroot-inl , u , v) ; //递归进入右子树，在中序中（左根右），右子树的右边界不变，右子树的左边界是根节点右边第一个，在先序中（根左右），右子树的根节点是当前根节点的下标+左子树长度+1

为什么要设置mp呢 
因为正常利用中序先序确定一棵树，需要找每棵子树根节点
暴力寻找要O(n)的时间,而本题的n最大为1e4,暴力的话显然会超时 

下面是代码 

#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e4 + 10 ;
const ll inf = 0x3f3f3f3f ;
const ll mod = 12345678901 ;
int a[maxn] , b[maxn] ;//中序，先序 
map<int , int > mp ;//中序结点对应下标
int ant = -1 ; //最近祖先 
void dfs(int inl , int inr , int preroot ,  int u , int v){
	if(inl > inr)return ;
	//inu,inv是u和v在中序中的下标 , inroot是当前子树根节点在中序中的下标 
	int inroot = mp[b[preroot]] , inu = mp[u] , inv = mp[v] ;
	if(inu >= inl && inu < inroot && inv >= inl && inv < inroot) {//若u和v在同一棵左子树 
		ant = b[preroot+1] ;
		dfs(inl , inroot-1 , preroot+1 , u , v) ; 
	}else if(inu > inroot && inu <= inr && inv > inroot && inv <= inr){//若u和v在同一棵右子树
		ant = b[preroot+1+inroot-inl] ;
		dfs(inroot+1 , inr , preroot+1+inroot-inl , u , v) ; 
	}else{//若u和v不在同一棵子树中,则lca就是当前根节点 
		ant = b[preroot] ;
		return ; 
	}
}
void deal(){
	int n , m ; cin >> m >> n ;
	for(int i = 1 ; i <= n ; i ++){
		cin >> a[i] ;
		mp[a[i]] = i ;
	}
	for(int i = 1 ; i <= n ; i ++){
		cin >> b[i] ;
	}
	for(int i = 0 ; i < m ; i++){
		ant = b[1] ;//一开始祖先都是根节点 
		int u ,v ; cin >> u >> v ;
		if(mp[u] == 0 && mp[v] == 0){
			printf("ERROR: %d and %d are not found.\n" , u , v) ;
		}else if(mp[u] == 0){
			printf("ERROR: %d is not found.\n" , u) ;
		}else if(mp[v] == 0){
			printf("ERROR: %d is not found.\n" , v) ;
		}else{
			dfs(1 , n , 1 , u , v) ;
			if(ant != u && ant != v)
				printf("LCA of %d and %d is %d.\n" , u , v , ant) ;
			else if(ant == u){
				printf("%d is an ancestor of %d.\n" , u , v) ;
			}else{
				printf("%d is an ancestor of %d.\n" , v , u) ;
			}
		}
	}
}
int main(){
    deal() ;
    return 0 ;
}