题面
A Marble Game is played with M marbles on a square board. The board is divided into N ×N unit squares, and M of those unit squares contain holes. Marbles and holes are numbered from 1 to M. The goal of the Marble game is to roll each marble into the hole that has the same number. A game board may contain walls. Each wall is one unit long and stands between two adjacent unit squares. Two squares are considered adjacent if and only if they share a side. At the beginning of the game, all marbles are placed on the board, each in a different square. A “move” consists of slightly lifting a side of the game board. Then all marbles on the board roll downward toward the opposite side, each one rolling until it meets a wall or drops into an empty hole, or until the next square is already occupied by another marble. Marbles roll subject to the following restrictions:
• Marbles cannot jump over walls, other marbles, or empty holes.
• Marbles cannot leave the board. (The edge of the board is a wall.)
• A unit square can contain at most a single marble at any one time.
• When a marble moves into a square with a hole, the marble drops into that hole. The hole is then filled, and other marbles can subsequently roll over the hole. A marble in a hole can never leave that hole.
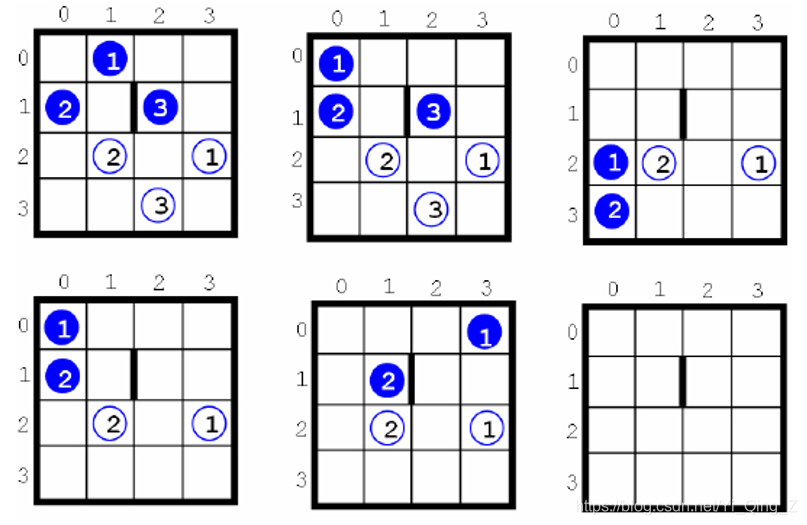
The game is over when each marble has dropped into a hole with the corresponding number. The figure below illustrates a solution for a game played on a 4×4 board with three blue marbles, three holes and a wall. The solution has five moves: lift the east side, lift the north side, lift the south side, lift the west side, lift the north side. Your program should determine the fewest number of moves to drop all the marbles into the correct holes — if such a move sequence is possible.
Input
The input file contains several test cases. The first line of each test case contains three numbers: the size N (2 ≤ N ≤ 4) of the board, the number M (M > 0) of marbles, and the number W of walls. Each of the following 2M lines contains two integers. The first integer is a row location and the second is a column location. The first M of those lines represent the locations of the marbles, where marble#1 is on the first line, marble#2 on the second, and so on. The last M of those lines represent the locations of the holes, with the location of hole#1 coming first, hole#2 coming second, and so on. Finally, the next W lines represent the wall locations. Each of those lines contains four integers: the first pair are the row and column of the square on one side of the wall and the second pair are the row and column of the square on the other side of the wall. Rows and columns are numbered 0..N −1. The input file ends with a line containing three zeroes.
Output
For each test case, print the case number (beginning with 1) and the minimal number of moves to win the game. If the game cannot be won, print the word ‘impossible’. Put a blank line after each test case. Use the format of the sample output below.
Sample Input
4 3 1
0 1
1 0
1 2
2 3
2 1
3 2
1 1 1 2
3 2 2
0 0
0 1
0 2
2 0
2 0 1 0
2 0 2 1
0 0 0
Sample Output
Case 1: 5 moves
Case 2: impossible
题目链接
参考链接
bfs UVA 1063 Marble Game Author: Killerfear
UVA 1063|11318|UVALive 3807|Marble Game|搜索 Author: huanghongxun MAP判重数组
题意简述
让小球滚进对应的洞,求最短步数。
当一个小球进到对应的洞时,可以把该洞填平,即其他球可以滚过该洞。
分析
模拟小球滚动,bfs搜索,用MAP判重数组
程序分析
int judge_board(Board x)/**判断球是否都进洞了**/
int deal(Board &b,int dir,Node now,Node next,bool &is_roll,bool &s_now,bool &s_next)/**将球滚到下一个位置**/
bool build_point(int dir,int i,int j,int k,Node &now,Node &next)/**判断球所在位置和将要滚到的位置是否合法**/
bool roll(Board &b,int dir)/**模拟球滚动的过程**/
void init_MAP()/**初始化MAP,在MAP边缘建围墙**/
void read()/**读入数据**/
int bfs()/**搜索求步数**/
程序
#include<stdio.h>
#include<iostream>
#include<map>
#include<queue>
#include<string.h>
using namespace std;
#define one if(build_point(dir,i,j,k,now,next)==false)break;
#define two d=deal(b,dir,now,next,is_roll,sign[MAP[now.x][now.y].hole],sign[MAP[next.x][next.y].hole]);
#define three if(d==0)break;else if(d==-1)return false;
int zx[]={-1,0,1,0};
int zy[]={0,1,0,-1};
int N,M,W;
struct Cube
{
int hole;
bool cant[4];
}MAP[5][5];
struct Board
{
int cu[4][4];
bool operator< (const Board &b) const
{
for(int i=0;i<4;i++)
for(int j=0;j<4;j++)
if (cu[i][j] != b.cu[i][j])
return cu[i][j] < b.cu[i][j];
return 0;
}
};
struct Node
{
int x,y;
Node(int X,int Y):x(X),y(Y){}
Node(){}
void change(int X,int Y){x=X,y=Y;}
bool ri()
{
if(x<0||x>=N||y<0||y>=N)
return false;
return true;
}
};
struct Board_s
{
Board x;
int step;
}ori;
int judge_board(Board x)
{
bool ans=true;
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
if(x.cu[i][j])
ans=false;
return ans;
}
int deal(Board &b,int dir,Node now,Node next,bool &is_roll,bool &s_now,bool &s_next)
{
if(next.x<0||next.x>=N||next.y<0||next.y>=N)
return 0;
if(now.x<0||now.x>=N||now.y<0||now.y>=N)
return 0;
if(MAP[now.x][now.y].cant[dir]||b.cu[next.x][next.y])/**有挡板**//**有球占住了**/
return 0;
if(MAP[now.x][now.y].hole&&!s_now)/**当前是个洞,且是错的洞**/
return -1;
if(MAP[next.x][next.y].hole==0)/**下一个位置不是洞**/
is_roll=true,swap(b.cu[now.x][now.y],b.cu[next.x][next.y]);
else/**下一个位置是洞**/
{
if(b.cu[now.x][now.y]==MAP[next.x][next.y].hole)/**进对洞了**/
{
is_roll=true,b.cu[now.x][now.y]=0,s_next=true;//将这个球从board上去掉
return 0;
}
if(s_next)/**洞被填上了**/
is_roll=true,swap(b.cu[now.x][now.y],b.cu[next.x][next.y]);
else/**进错洞了**/
return -1;
}
return 1;
}
bool build_point(int dir,int i,int j,int k,Node &now,Node &next)
{
now.change(i+zx[dir]*k,j+zy[dir]*k);
next.change(now.x+zx[dir],now.y+zy[dir]);
if(now.ri()==false||next.ri()==false)
return false;
return true;
}
bool roll(Board &b,int dir)
{
bool is_roll=false;
bool sign[17];
Node now,next;
int d;
for(int i=0;i<17;i++)
sign[i]=true;
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
{
if(b.cu[i][j]==MAP[i][j].hole)
b.cu[i][j]=0;
sign[b.cu[i][j]]=false;
}
if(dir==0)
{
for(int j=0;j<N;j++)
for(int i=0;i<N;i++)
if(b.cu[i][j])
for(int k=0;k<N;k++)
{ one two three }
}
else if(dir==1)
{
for(int i=0;i<N;i++)
for(int j=N-1;j>=0;j--)
if(b.cu[i][j])
for(int k=0;k<N;k++)
{ one two three }
}
else if(dir==2)
{
for(int j=0;j<N;j++)
for(int i=N-1;i>=0;i--)
if(b.cu[i][j])
for(int k=0;k<N;k++)
{ one two three }
}
else//dir==3
{
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
if(b.cu[i][j])
for(int k=0;k<N;k++)
{ one two three }
}
return is_roll;
}
void init_MAP()
{
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
{
MAP[i][j].hole=0;
memset(MAP[i][j].cant,0,sizeof(MAP[i][j].cant));
}
for(int i=0;i<N;i++)
{
MAP[0][i].cant[0]=true;
MAP[i][N-1].cant[1]=true;
MAP[N-1][i].cant[2]=true;
MAP[i][0].cant[3]=true;
}
return;
}
void read()
{
int row,column,an_row,an_column,x1,x2,y1,y2;
memset(ori.x.cu,0,sizeof(ori.x.cu));
for(int i=1;i<=M;i++)
{
scanf("%d%d",&row,&column);
ori.x.cu[row][column]=i;
}
ori.step=0;
for(int i=1;i<=M;i++)
{
scanf("%d%d",&row,&column);
MAP[row][column].hole=i;
}
for(int i=0;i<W;i++)
{
scanf("%d%d%d%d",&row,&column,&an_row,&an_column);
if(row==an_row)
{
MAP[row][min(column,an_column)].cant[1]=true;
MAP[row][max(column,an_column)].cant[3]=true;
}
else
{
MAP[min(row,an_row)][column].cant[2]=true;
MAP[max(row,an_row)][column].cant[0]=true;
}
}
}
int bfs()
{
bool temp=true;
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
{
if(ori.x.cu[i][j]!=MAP[i][j].hole)
temp=false;
else
ori.x.cu[i][j]=0;
}
if(temp)
return 0;
queue<Board_s>q;
map<Board,int>visit;
q.push(ori);
Board_s now,next;
while(!q.empty())
{
now=q.front();
q.pop();
for(int i=0;i<4;i++)
{
next=now;
next.step++;
bool re=roll(next.x,i);
if(re==false)//滚不动
continue;
bool j=judge_board(next.x);
if(j==true)
return next.step;
else/**j==0**/if(!visit[next.x])
{
visit[next.x]=1;
q.push(next);
}
}
}
return -1;
}
int main()
{
int e=1;
while(scanf("%d%d%d",&N,&M,&W)&&(N||W||W))
{
init_MAP();
read();
int answer=bfs();
printf("Case %d: ",e++);
if(answer==-1)
printf("impossible\n");
else
printf("%d moves\n",answer);
printf("\n");
}
return 0;
}//show函数
void show_Board_s(Board_s b)
{
printf("step=%d\n",b.step);
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
printf("%d ",b.x.cu[i][j]);
printf("\n");
}
printf("\n");
}
void show_Board(Board b)
{
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
printf("%d ",b.cu[i][j]);
printf("\n");
}
printf("\n");
}
样例
4 8 9
0 0
1 0
2 0
3 0
3 1
3 2
3 3
2 31 2
2 2
2 1
1 1
0 1
0 2
0 3
1 30 0 0 1
1 0 1 1
2 0 2 1
2 1 3 1
2 2 3 2
2 2 2 3
1 2 1 3
0 2 1 2
1 1 1 225 moves
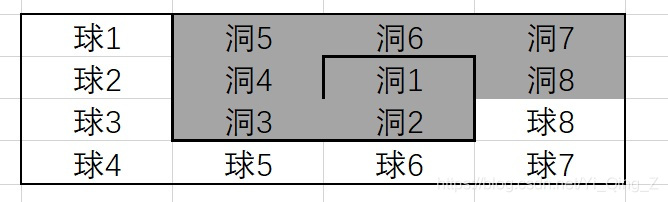







 本文详细解析UVA_1063 Marble Game的解题思路,介绍了一种利用BFS搜索算法解决迷宫类问题的方法。通过模拟小球在有障碍物的棋盘上滚动并进入指定洞口的过程,文章提供了完整的C++代码实现,并解释了如何使用MAP数组进行状态判重,确保搜索效率。
本文详细解析UVA_1063 Marble Game的解题思路,介绍了一种利用BFS搜索算法解决迷宫类问题的方法。通过模拟小球在有障碍物的棋盘上滚动并进入指定洞口的过程,文章提供了完整的C++代码实现,并解释了如何使用MAP数组进行状态判重,确保搜索效率。
















 1251
1251

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








