1. 队列的概念和性质
1.1 定义:
队列是一种有次序的数据集合,其特征是
- 新数据项的添加总发生在一端(通常称为“尾rear”端)
- 而现存数据项的移除总发生在另一端(通常称为“首front”端)
当数据项加入队列,首先出现在队尾,随着队首数据项的移除,它逐渐接近队首。

1.2 性质:
- FIFO First-in first-out 先进先出:新加入的数据项必须在数据集末尾等待,而等待时间最长的数据项则是队首
- 队列仅有一个入口和一个出口:不允许数据项直接插入队中,也不允许从中间移除数据项
1.3 例子:
- 排队:上银行办业务,先到的人排在前面,先接受服务。后面的人后接受服务。
2. 数据结构中的队列Queue
在数据结构中,我们用Queue这种抽象数据类型表示队列。
2.1 定义:
抽象数据类型Queue由如下操作定义:
- Queue():创建一个空队列对象,返回值为Queue对象;
- enqueue(item):将数据项item添加到队尾,无返回值;即入队。
- dequeue():从队首移除数据项,返回值为队首数据项,队列被修改;即出队
- isEmpty():测试是否空队列,返回值为布尔值
- size():返回队列中数据项的个数。
2.2 例子
例如
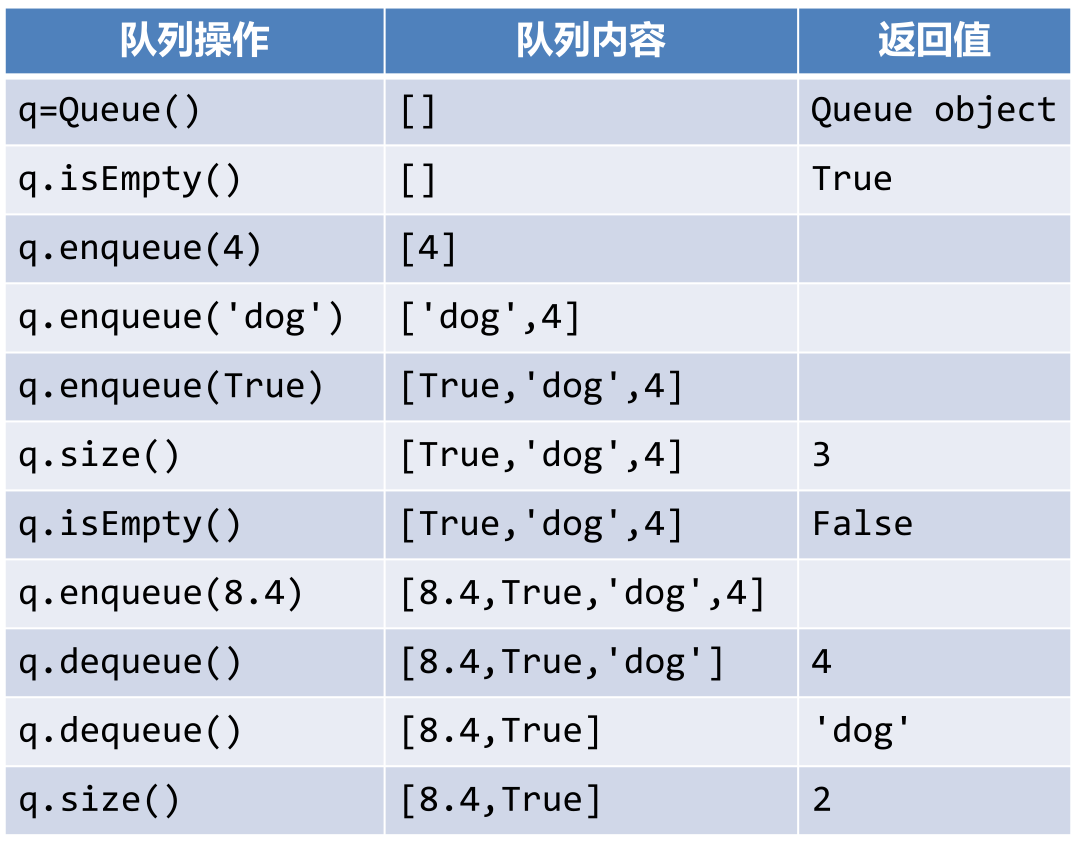
2.3 代码实现Queue
class Queue:
def __init__(self):
self.items = []
def enqueue(self, item): # 复杂度是 O(n)
self.items.insert(0, item) # 即,列表的最左端作为队尾,这是和栈最关键的区别
def dequeue(self): # 复杂度是 O(1)
return self.items.pop() # 即,列表的最右端作为队尾,这和栈是一样的
def isEmpty(self):
return self.items == []
def size(self):
return len(self.items)
# 测试
q = Queue()
q.enqueue("xxx")
print(q.items)
print(q.isEmpty())
print(q.size())
print(q.dequeue())
print(q.items)
print(q.isEmpty())
print(q.size())
3. 双端队列Deque
3.1 定义
双端队列是一种特殊的队列,这种队列数据项既可以从队首加入,也可以从
队尾加入;数据项也可以从两端移除。
某种意义上说,双端队列集成了栈和队列的能力
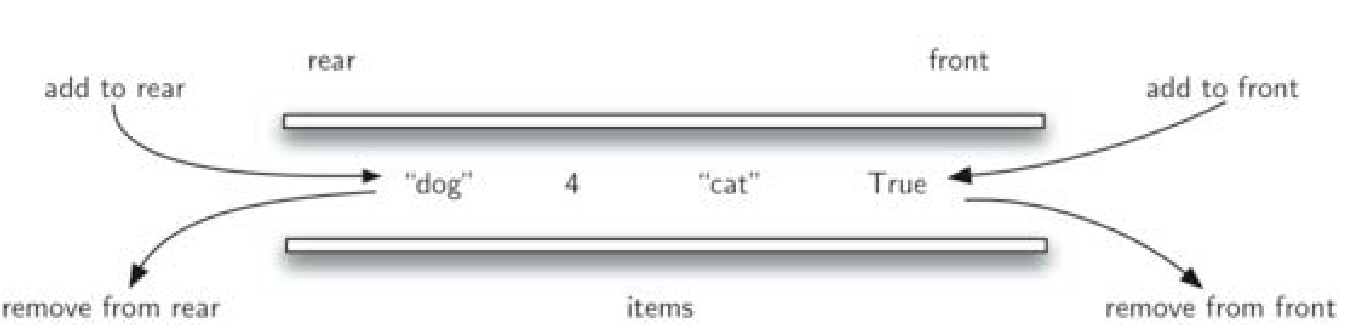
3.2 性质
双端队列并不具有内在的L IFO或者FIFO特性
如果用双端队列来模拟栈或队列,需要由使用者自行维护操作的一致性
4. 数据结构中的Deque
4.1 定义:
deque定义的操作如下:
- Deque():创建一个空双端队列
- addFront(item):将item加入队首
- addRear(item):将item加入队尾
- removeFront():从队首移除数据项,返回值为移除的数据项
- removeRear():从队尾移除数据项,返回值为移除的数据项
- isEmpty():返回deque是否为空
- size():返回deque中包含数据项的个数
4.2 例子
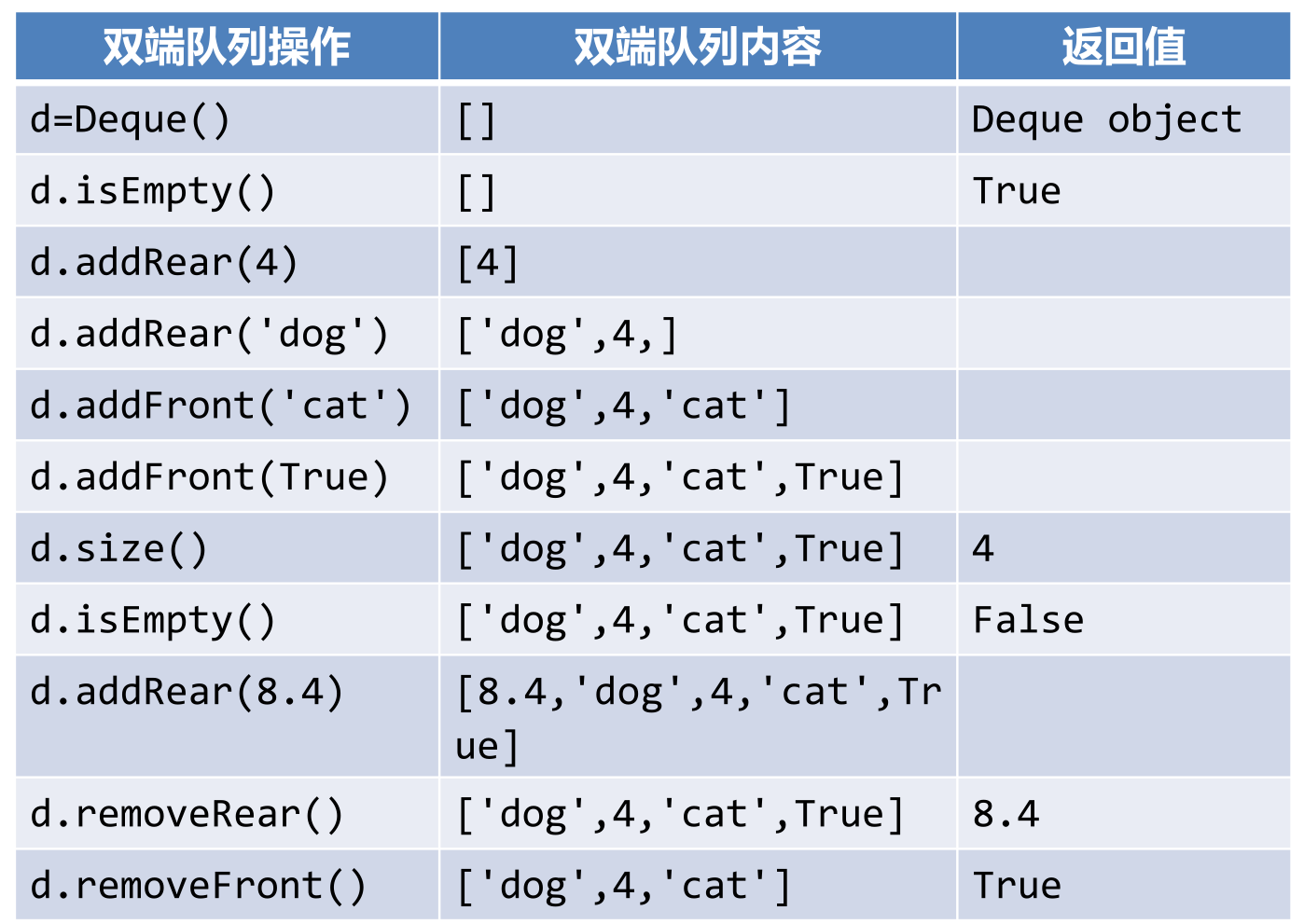
4.3 代码实现Deque
class Deque:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def addFront(self, item):
self.items.append(item)
def addRear(self, item):
self.items.insert(0, item)
def removeFront(self):
return self.items.pop()
def removeRear(self):
return self.items.pop(0)
def size(self):
return len(self.items)
5. 算法题:判断回文词:
5.1 问题:
“回文词”指正读和反读都一样的词,
如radar、madam、toot
中文“上海自来水来自海上”,“山东落花生花落东山”
5.2 解:
解一:
通过观察,每个词的字母构成都是左右对称的。我们使用双端队列存储每一个词的所有字母。字母从两端出队,当队列为空,或只剩下一个字母的时候,两端出队的字母相同,则是回文词。
class Deque:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def addFront(self, item):
self.items.append(item)
def addRear(self, item):
self.items.insert(0, item)
def removeFront(self):
return self.items.pop()
def removeRear(self):
return self.items.pop(0)
def size(self):
return len(self.items)
def huiWenci(wordList):
dq = Deque()
for ch in wordList:
dq.addRear(ch)
stillEqual = True
while dq.size() > 1 and stillEqual:
first = dq.removeFront()
last = dq.removeRear()
if first != last:
stillEqual = False
return stillEqual
print(huiWenci("radar")) # True
print(huiWenci("toot")) # True
print(huiWenci("上海自来水来自海上")) # True
print(huiWenci("山东落花生花落东山")) # True
print(huiWenci("toor")) # False
print(huiWenci("山东落花生花落西山")) # False
解二:
也是队列的思想,但是直接使用列表
先把词存入到列表当中,
对比列表的左右两端是否相同,
如果相同则将他们移出列表,继续对比
如果不同就判断出不是回文词
如果最后列表为空或者是只剩一个字母,就说明是回文词
huiwen_word = input()
huiwen_word = list(huiwen_word)
def is_huiwen(huiwen_word):
result = True
while len(huiwen_word) > 1:
if huiwen_word[0] == huiwen_word[-1]:
huiwen_word.pop(0)
huiwen_word.pop()
else:
result = False
break
return result
print(is_huiwen(huiwen_word))
6. 算法题:热土豆(约瑟夫)问题
6.1 问题:
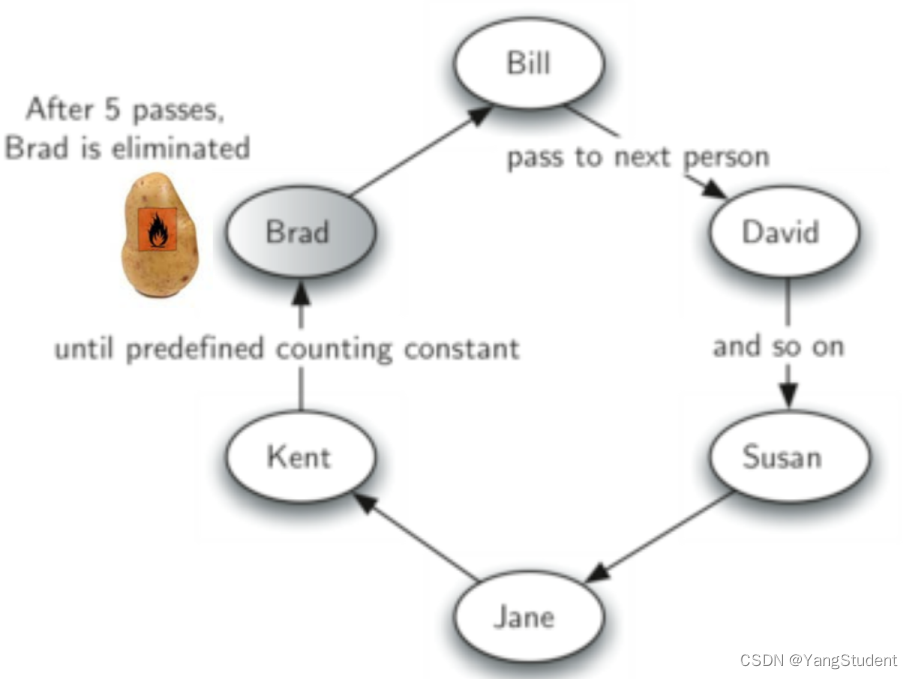
热土豆问题也称约瑟夫问题。
热土豆问题就是大家传递一个土豆,规定一个计数n,第一个人拿着土豆的时候他的计数就是1,当第n个人拿到土豆的时候,他就出局,然后他的下一个人计数被重置为1。如此反复,请问最后是谁还没出局。
约瑟夫问题的说法就是,规定计数为n,有几个人轮流报数,从1开始报数到n,报数为n的人自杀。请问最后是谁还活着。
输入:人名列表names,规定计数num输出:最后剩下的人的名字
6.2 解:
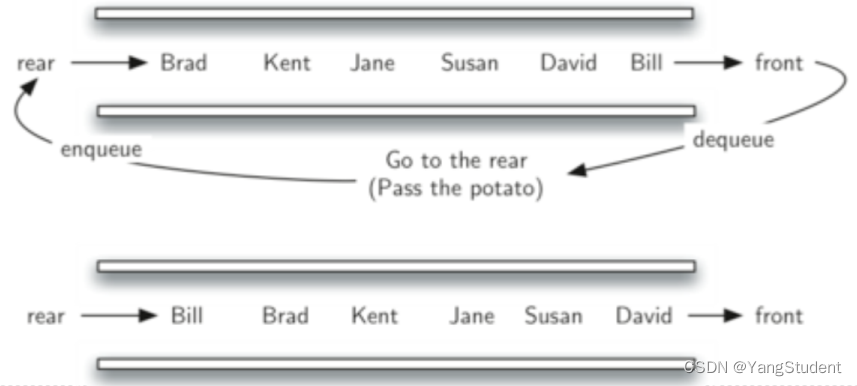
用队列来完成任务。
用队列存放所有人名,按照传递土豆的方向从队首排到队尾。队首的人始终是拿着土豆的人。
将队首的人出队再在队尾入队,就是土豆的一次传递。
传递num次后,将队首的人出队,不再入队,如此反复直到最后只剩一个人
写法一:
def hot_potato(names, num):
count = 1 # 初始状态是1,因为第一个人开始就拿着土豆
while len(names) > 1:
if count != num: # count 等于 num 时, 报数就报到那个人了
names.append(names.pop(0))
count = count + 1 # 传给下个人的时候,下个人的报数比上一个+1
else:
names.pop(0)
count = 1
return names
print(hot_potato(["Bill", "David", "Susan", "Jane", "Kent", "Brad"], 7))
写法二:
def hot_potato(names, num):
q = []
for name in names: # 先把所有的人名都存入队列,当然其实直接用names作为队列也行
q.append(name)
while len(q) > 1: # 队列最后剩下的那个是幸运儿
for i in range(num): # 从 0 到 num-1
q.append(q.pop(0)) # 队头的人挪到队尾,完成一次传递
q.pop() # 他的报数是第num个,他出队
return q.pop()
print(hot_potato(["Bill", "David", "Susan", "Jane", "Kent", "Brad"], 7))
7. 打印任务
7.1 问题:
多人共享同一台打印机,采用“先到先服务”的队列策略执行打印任务。
在这种设定下,首要的问题是:
这种打印作业系统的容量有多大?
在能够接受的等待时间内,系统能容纳多少用户以多高频率提交打印任务?
一个具体配置如下:
一个实验室,在任意的一个小时内,大约有10名学生在场,这一小时中,每人会发起2次左右的打印,每次1~20页
打印机的性能:
以草稿模式打印的话,每分钟10页,以正常模式打印的话,打印质量好,但速度下降为每分钟5页
请问:
怎么设定打印机的模式,让大家都不会等太久的前提下尽量提高打印质量?
分析:
这是一个典型的决策支持问题,但无法通过规则直接计算。
我们要用一段程序来模拟这种打印任务场景,然后对程序运行结果进行分析,以支持对打印机模式设定的决策
7.2 如何对问题建模?
首先对问题进行抽象,确定相关的对象和过程
抛弃那些对问题实质没有关系的学生性别、年龄、打印机型号、打印内容、纸张大小等等众多细节
对象:打印任务、打印队列、打印机
打印任务的属性:提交时间、打印页数
打印队列的属性:具有FIFO性质的打印任务队列
打印机的属性:打印速度、是否忙
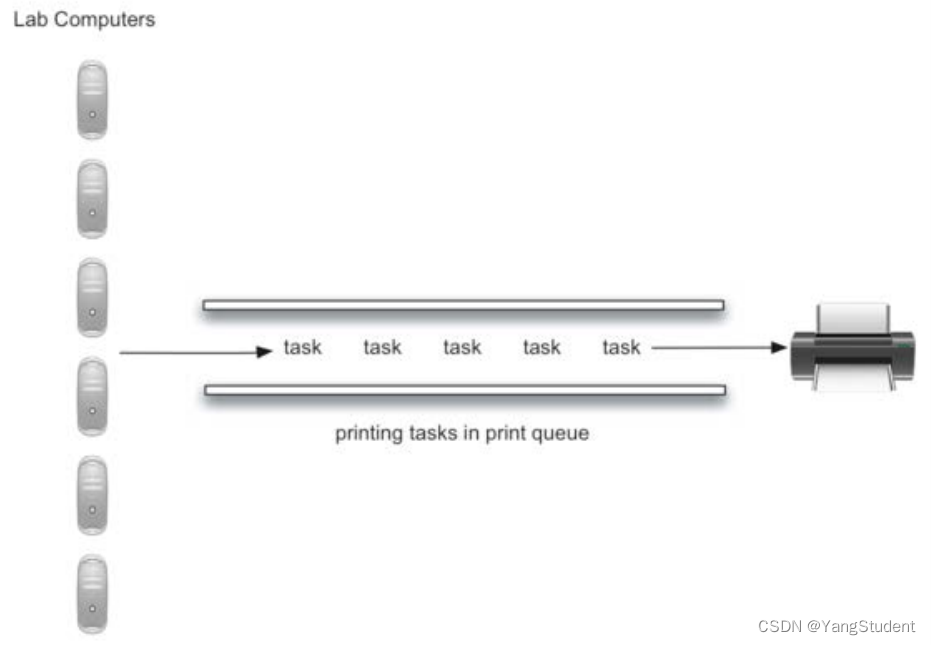
过程:生成和提交打印任务
确定生成概率:实例为每小时会有10个学生提交的20个作业,这样,概率是每180秒会有1个作业生成并提交,概率为每秒1/180。
确定打印页数:实例是1~20页,那么就是1~20页之间概率相同。
过程:实施打印
当前的打印作业:正在打印的作业
打印结束倒计时:新作业开始打印时开始倒计时,回0表示打印完毕,可以处理下一个作业
模拟时间:
统一的时间框架:以最小单位(秒)均匀流逝的时间,设定结束时间
同步所有过程:在一个时间单位里,对生成打印任务和实施打印两个过程各处理一次
打印任务的流程:
-
创建打印队列对象
-
时间按照秒的单位流逝
按照概率生成打印作业,加入打印队列
如果打印机空闲,且队列不空,则取出队首作业打印,记录此作业等待时间
如果打印机忙,则按照打印速度进行1秒打印
如果当前作业打印完成,则打印机进入空闲 -
时间用尽,开始统计平均等待时间
-
作业的等待时间:
生成作业时,记录生成的时间戳
开始打印时,当前时间减去生成时间即可 -
作业的打印时间
生成作业时,记录作业的页数
开始打印时,页数除以打印速度即可
7.3 实现
import random
class Printer: # 打印机类
def __init__(self, ppm):
self.page_rate = ppm # ppm 是打印机的打印速度,1秒打印ppm页
self.current_task = None # 当前的打印任务
self.time_remaining = 0 # 倒计时
def tick(self): # 打印1秒
if self.current_task is not None: # 当打印机在打印的时候
self.time_remaining = self.time_remaining - 1 # 这个任务的倒计时-1
if self.time_remaining <= 0: # 倒计时小于等0时,表示当前打印任务结束
self.current_task = None
def busy(self): # 打印机是否在忙
if self.current_task is not None: # 当前有任务就在忙
return True
else:
return False
def start_next(self, new_task):
self.current_task = new_task # 新任务来时,重置为新任务
self.time_remaining = new_task.get_pages() * 60 / self.page_rate # 新任务的剩余时间
class Task: # 打印任务
def __init__(self, time):
self.time_stamp = time # 当前时间戳
self.pages = random.randrange(1, 21) # 这个任务随机打印 1 - 20页
def get_stamp(self): # 返回当前时间戳
return self.time_stamp
def get_pages(self): # 返回当前任务需要打印的页数
return self.pages
def wait_time(self, current_time): # 等待的时间
return current_time - self.time_stamp
def new_print_task():
num = random.randrange(1, 181) # 1/180的概率生成新作业
if num == 180:
return True
else:
return False
def simulation(num_seconds, page_per_minute): # 模拟打印机
lab_printer = Printer(page_per_minute) # 实验室的打印机
print_queue = [] # 用列表模拟队列
waiting_times = [] # 任务的等待的时间
for current_second in range(num_seconds): # 每一秒
if new_print_task(): # 如果有新的作业
task = Task(current_second)
print_queue.append(task) # 让任务进队
if (not lab_printer.busy()) and (len(print_queue) > 0): # 打印机空闲,且有打印任务在队中
next_task = print_queue.pop(0)
waiting_times.append(next_task.wait_time(current_second)) # 新任务的等待时间存入到列表
lab_printer.start_next(next_task) # 打印机打印下一个任务
lab_printer.tick() # 减少倒计时
average_wait = sum(waiting_times) / len(waiting_times)
print("Average wait %6.2f secs %3d tasks remaining." %(average_wait, len(print_queue)))
for i in range(10):
simulation(3600, 5)
for i in range(10):
simulation(3600, 10)
7.4 结果分析
时间设置为1小时,ppm设置为5,运行10次
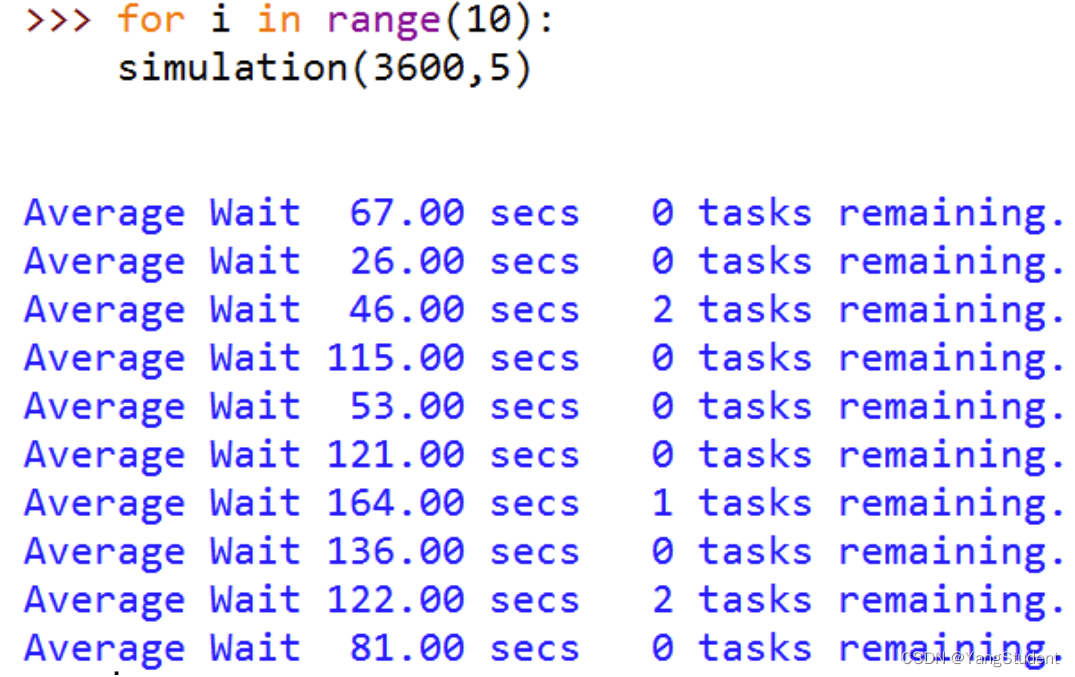
有3次模拟,还有作业没开始打印
提升打印速度到10PPM、1小时的设定
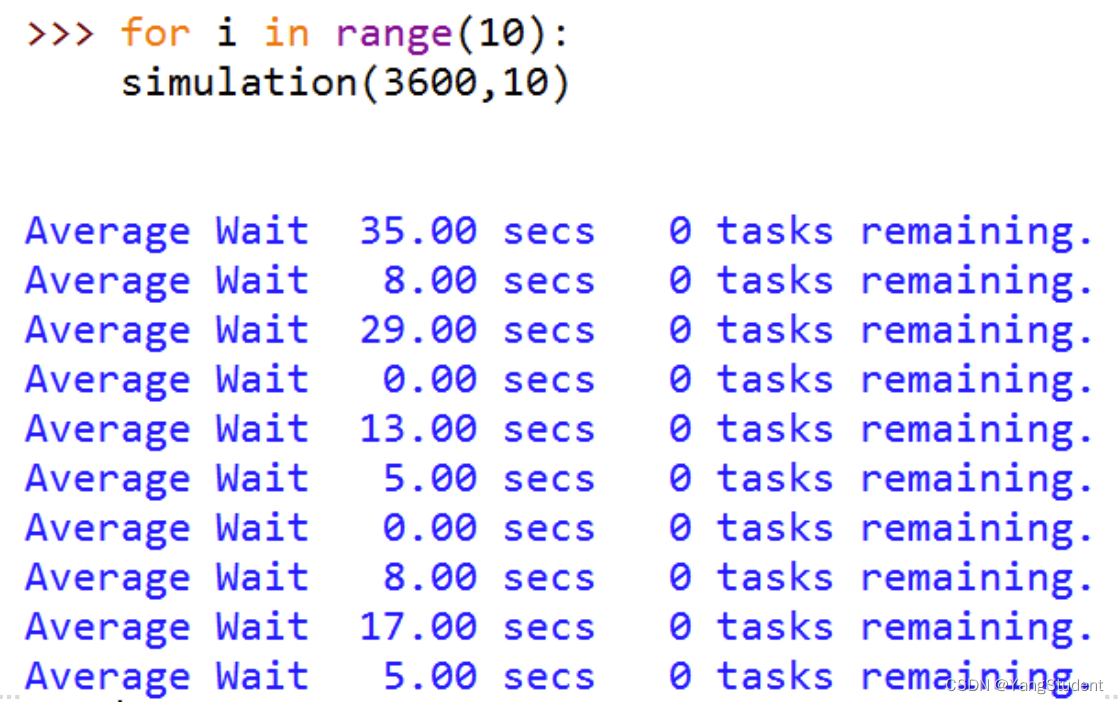
7.5 讨论
为了对打印模式设置进行决策,我们用模拟程序来评估任务等待时间
通过两种情况模拟仿真结果的分析,我们认识到如果有那么多学生要拿着打印好的程序源代码赶去上课的话。那么,必须得牺牲打印质量,提高打印速度。
模拟系统对现实的仿真
在不耗费现实资源的情况下——有时候真实的实验是无法进行的
可以以不同的设定,反复多次模拟来帮助我们进行决策
更真实的模拟,来源于对问题的更精细建模,以及以真实数据进行设定和运行
也可以扩展到其它类似决策支持问题
如:饭馆的餐桌设置,使得顾客排队时间变短
参考文献
本文的知识来源于B站视频 【慕课+课堂实录】数据结构与算法Python版-北京大学-陈斌-字幕校对-【完结!】,是对陈斌老师课程的复习总结





















 677
677










