博客主要介绍了LSTM的相关内容，包括其一般结构，如遗忘门层、输入门层和输出门层的具体公式及作用，还提及了LSTM的一些变形，如将Ct−1考虑进来和默认it=1−ft的情况。此外，还介绍了门控循环单元（GRU）的特点和细节。
LSTM
一般结构
Forget Gate Layer
Detail
f
t
=
σ
(
W
f
∗
[
h
t
−
1
,
x
t
]
+
b
f
)
f_{t}=\sigma (W_{f}*[h_{t-1},x_{t}]+b_f)
ft=σ(Wf∗[ht−1,xt]+bf)
决定信息保留程度,“1”代表完全保留，“0”代表完全舍弃
Input Gate Layer
Detail
i
t
=
σ
(
W
i
∗
[
h
t
−
1
,
x
t
]
+
b
i
)
i_t=\sigma (W_i*[h_{t-1},x_t]+b_i)
it=σ(Wi∗[ht−1,xt]+bi)
C
t
′
=
t
a
n
h
(
W
i
∗
[
h
t
−
1
,
x
t
]
+
b
i
)
C_t^{'}=tanh (W_i*[h_{t-1},x_t]+b_i)
Ct′=tanh(Wi∗[ht−1,xt]+bi)
Next
C t = f t ∗ C t − 1 + i t ∗ C t ′ C_t=f_t*C_{t-1}+i_t*C_t{'} Ct=ft∗Ct−1+it∗Ct′
Output Gate Layer
Detail
o
t
=
σ
(
W
o
∗
[
h
t
−
1
,
x
t
]
+
b
o
)
o_t=\sigma (W_o*[h_{t-1},x_t]+b_o)
ot=σ(Wo∗[ht−1,xt]+bo)
h
t
=
o
t
∗
t
a
n
h
(
C
t
)
h_t=o_t*tanh (C_t)
ht=ot∗tanh(Ct)
一些变形
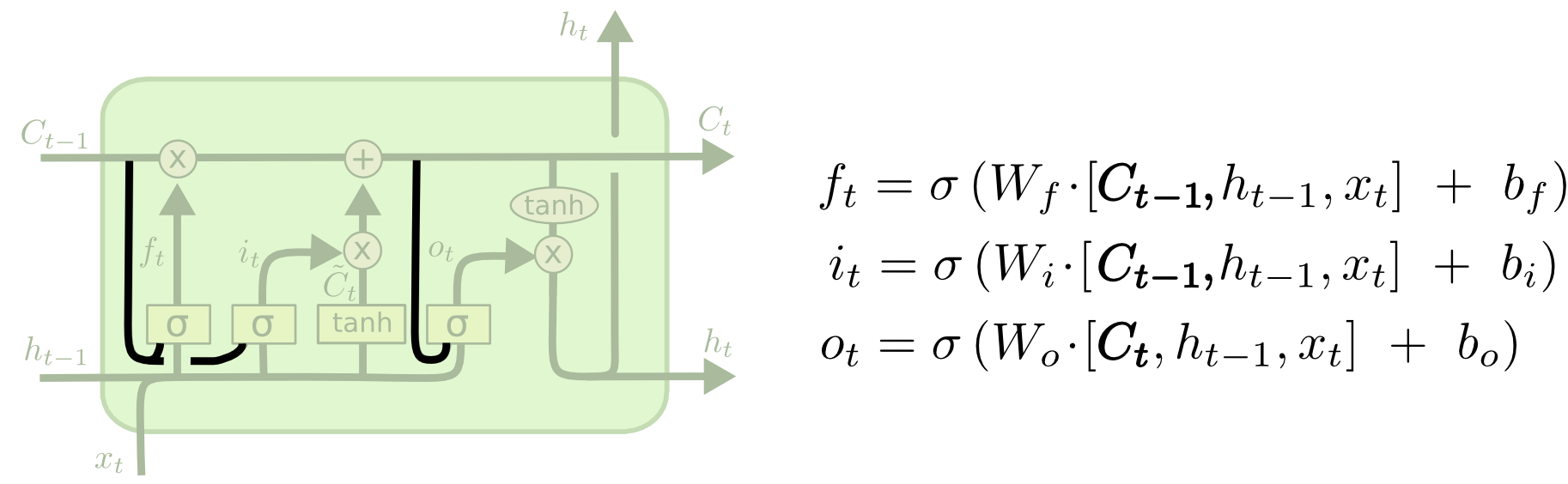
将 C t − 1 C_{t-1} Ct−1考虑进来
f
t
=
σ
(
W
f
∗
[
h
t
−
1
,
x
t
,
C
t
−
1
]
+
b
f
)
f_{t}=\sigma (W_{f}*[h_{t-1},x_{t},C_{t-1}]+b_f)
ft=σ(Wf∗[ht−1,xt,Ct−1]+bf)
i
t
=
σ
(
W
i
∗
[
h
t
−
1
,
x
t
,
C
t
−
1
]
+
b
i
)
i_t=\sigma (W_i*[h_{t-1},x_t,C_{t-1}]+b_i)
it=σ(Wi∗[ht−1,xt,Ct−1]+bi)
o
t
=
σ
(
W
o
∗
[
h
t
−
1
,
x
t
,
C
t
−
1
]
+
b
o
)
o_t=\sigma (W_o*[h_{t-1},x_t,C_{t-1}]+b_o)
ot=σ(Wo∗[ht−1,xt,Ct−1]+bo)
默认 i t = 1 − f t i_t=1-f_t it=1−ft
C
t
=
f
t
∗
C
t
−
1
+
(
1
−
f
t
)
∗
C
t
′
C_t=f_t*C_{t-1}+(1-f_t)*C_t{'}
Ct=ft∗Ct−1+(1−ft)∗Ct′
Gated Recurrent Unit(GRU)
特点
- 使用update gate代替forget & input gate
- 合并cell state 和 hidden state
Details
扫一扫
2175
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
