今天为大家介绍的是隐马尔可夫模型(Hidden Markov Model),隐马尔可夫模型最初是在20世纪60年代后半期Leonard E. Baum和其它一些作者在一系列的统计学论文中描述的。HMM最初的应用之一是开始于20世纪70年代中期的语音识别。
隐马尔可夫模型
简单介绍
隐马尔可夫模型是关于时序(顺序)的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测而产生观测随机序列的过程。隐藏的马尔可夫链随机生成的状态的序列,称为状态序列(state sequence);每个状态生成一个观测,而由此产生的观测的随机序列,称为观测序列(observation sequence)。序列的每一个位置又可以看作是一个时刻。
我们知道句子的表达不仅与其构成的词语有关,还与词的位置以及语法有关。因此对于语言来说,如果忽略语序进行理解,往往得不到句子正常的意思。(尽管如此,朴素贝叶斯在垃圾邮件分类上仍取得很好的效果)HMM在建立模型的时候可以考虑之前状态对当前的影响。例如,我们要给以下句子做词性标注
我(名词)爱(动词)学习(名词/动词?)
如果单独去给『学习』这个词标注的话,『学习』可能是名词也可以是动词。但在上面那句话里『学习』显然是名词,因为学习前面的词『爱』是动词,后面应该接名词,因此『学习』标注应该标注为名词。这里我们在标注的时候考虑前面词语的词性对当前词的词性的影响。HMM也是这样去给词语标注词性的。只不过HMM是这么看待以上问题,我 爱 学习 被看做长度为3的序列,这个序列为观测序列。它们的词性可以理解为词语的某个状态,由于我们现在是要给词语做标注,因此我们是不知道每个观测值(词语)的状态(词性)的。并且我们知道句子的基本构成有主谓宾定状补,词语的词性往往与该词在句子充当的成分有关。例如谓语(爱)之后的词(学习)很有可能名词这么一种转态改变的规则。
用HMM的概念来说,我爱学习是观测序列,词语的词性序列是一个状态序列,词性变化规则为状态转移矩阵(描述不同状态相互转换的概率)。在深入介绍隐马尔可夫模型之前先引入一些基本概念。
马尔可夫性
马尔可夫性质是概率论中的一个概念。当一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态;换句话说,在给定现在状态时,它与过去状态(即该过程的历史路径)是条件独立的,那么此随机过程即具有马尔可夫性质。具有马尔可夫性质的过程通常称之为马尔可夫过程。当前情况尽跟之前n个状态有关的随机过程称为n阶马尔科夫过程。
例子
拿天气和海藻的例子来说
假设海藻的湿度与天气有某种关联,为了简易的去定义这个问题,定义海藻存在四种观测值{dry,dryish,damo,soggy},天气的状态也只有三种状态{sunny,cloudy,rainy}。
(这里我们直接定义了观测序列为一段时间内,海藻的湿度的一个序列,隐含状态为同一段时间内,天气的状态序列,我们假设一个盲人只能通过触摸判断海藻湿度来推测天气这么一个情景)
在不同天气下,观测到海藻不同的湿度的概率是不同的
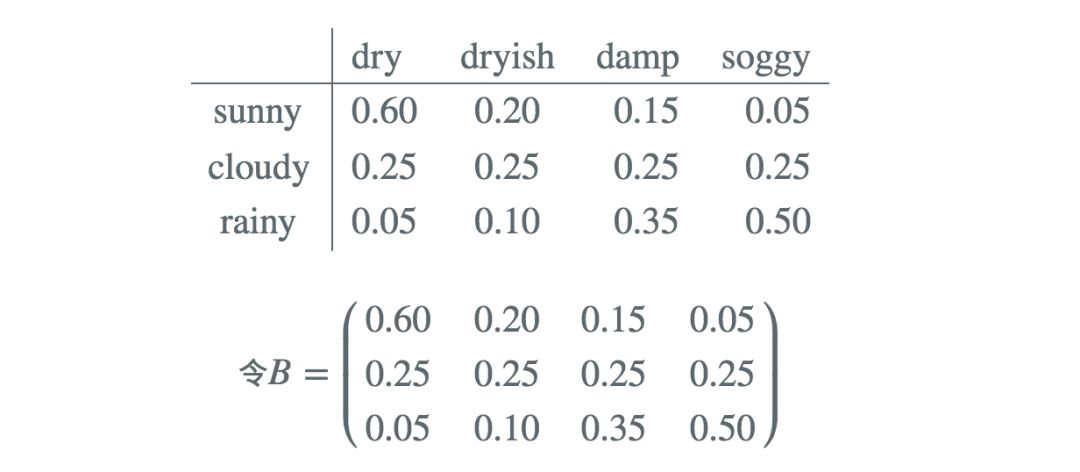
上面其实是一个观测矩阵,表示在不同的隐含状态下观测到不同海藻湿度的概率,你会发现该矩阵每一行求和的结果都等于1。这个矩阵的数据是通过经验获得的,例如你统计了很多个晴天的状态下,海藻有着不一样的湿度,通过对大量数据的一个统计,我们就可以得到晴天状态下,观测到不同湿度的海藻的概率。
当然天气之间也是存在互相转化的,但令人头疼的是,昨天的天气或者更久以前的天气会对今天的天气有所影响,这样考虑问题会使得问题变得格外复杂,因此隐马尔可夫做了最基本的假设,即当前状态只与前一个状态有关(齐次马尔可夫性假设)。同时也做观测独立性假设,所有的观测之间是互相独立的,某个观测之和生成它的状态有关系。
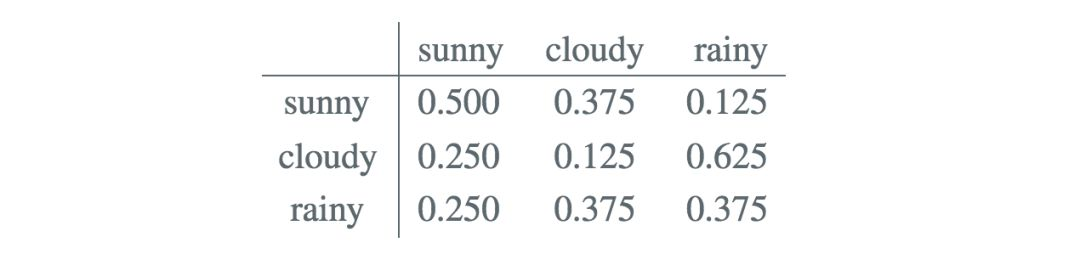
对应状态转移矩阵A

其中![]() 为状态:i->j的概率,然后同样你会发现每一行元素的求和等于1。
为状态:i->j的概率,然后同样你会发现每一行元素的求和等于1。
我们还需要序列的初始状态π,这个初始状态可以通过对多个样本的初始状态进行统计得出。
由此我们就已经定义了一个完整的隐马尔可夫模型,该模型由观测序列、状态序列、以及初始状态概率向量ππ、状态转移概率矩阵AA和观测概率矩阵BB,其中后三个为隐马尔可夫模型的参数一般用一个三元组表示。即
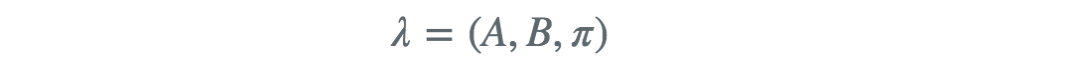
假设盲人连续记录三天,得到观察序列Q = {dry,damp,soggy},这三天的天气为{sunny,cloudy,rainy}(尽管盲人无法观测到,但可以通过马尔可夫模型去估计这几天的天气)
隐马尔可夫三个基本问题
概率计算问题:给定模型参数和观测序列,计算出现某个观测序列的概率
预测问题:给定模型参数和观测序列,求最有可能的状态序列
学习问题:给定观测序列和状态序列,得到模型参数
概率计算问题
给定模型参数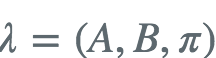 和观测序列
和观测序列 计算观测序列O的出现概率,直接计算即按照概率公式去计算
计算观测序列O的出现概率,直接计算即按照概率公式去计算 。
。
如果直接去计算,通过列举所有可能的长度为T的状态序列I,求各个状态序列I与观测序列的联合概率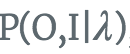 ,然后对所有可能的状态序列求和得到结果
,然后对所有可能的状态序列求和得到结果
对于给定的I序列,O,I同时出现的联合概率为
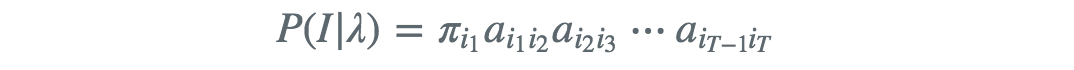
然后,对所有可能的状态序列I求和,得到观测序列O的概率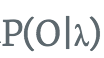
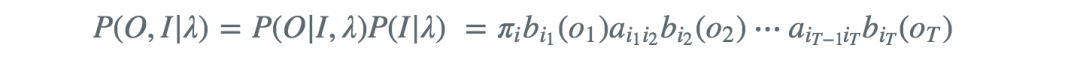
利用上述公式计算量很大,因为所有可能的状态序列有很多种,上述方法时间复杂度是 的,这种算法在数据量大的情况下,是不可行的。因此我们用前向算法去计算其时间复杂度为
的,这种算法在数据量大的情况下,是不可行的。因此我们用前向算法去计算其时间复杂度为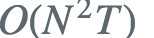 。
。
前向算法
前向概率 :给定隐马尔可夫模型参数λ 定义时刻t部分观测序列为
 ,且状态为
,且状态为![]() 的概率为前向概率,记作
的概率为前向概率,记作

每次计算利用了前一时刻N个状态下的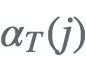 ,避免了重复计算
,避免了重复计算
前向算法其实是以空间换时间的一种方法。具体的第一项的前向概率为
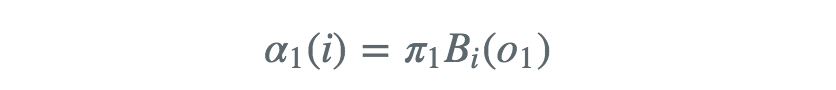
后面的项的前向概率为
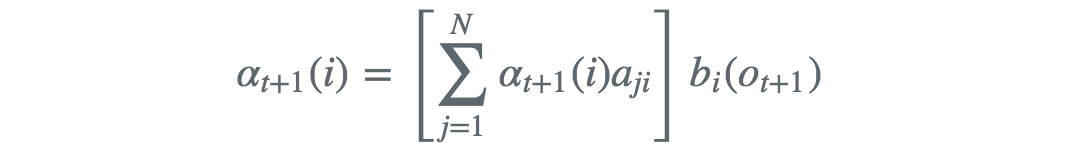
因此得出
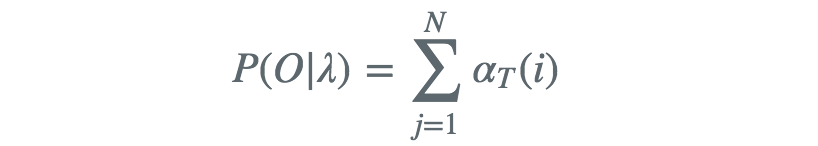
同理我们可以导出后向概率与后向算法
后向算法的从序列后面开始计算概率,最后一项的后项概率为
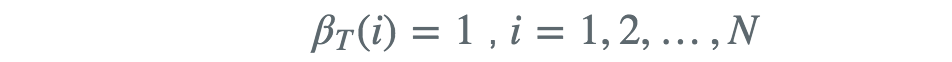
其余项的后向概率表示为
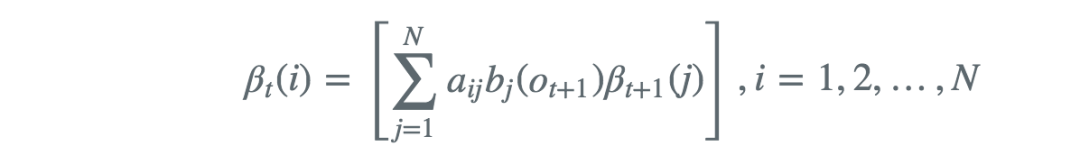
得出
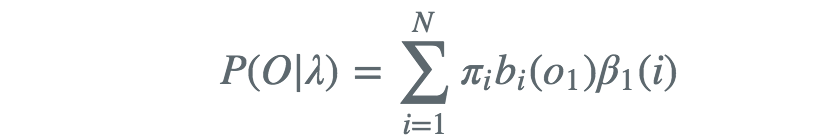
利用前向概率和后向概率的定义可以将概率统一写成
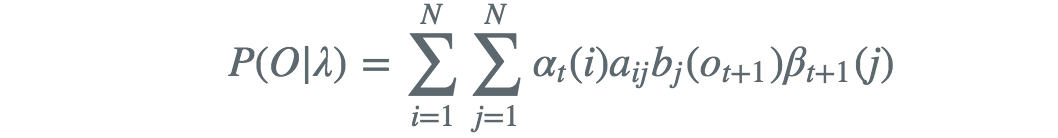
此式当t = 1 和 t = T -1时,则分别写为原来的形式
学习问题
监督学习问题
如果训练数据包含S个长度的长度的观测序列和对隐状态序列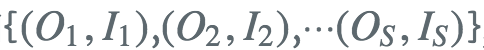 那么我们可以直接用极大似然估计隐马尔可夫模型的参数其中
那么我们可以直接用极大似然估计隐马尔可夫模型的参数其中
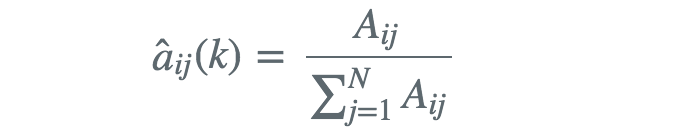
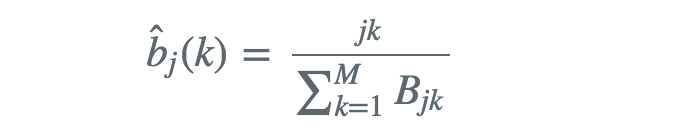
π̂ 为需要统计S个样本中初始状态为![]() 的概率。
的概率。
监督学习需要大量的数据,而且人工标注训练数据的代价往往很高,故有时就会利用非监督学习的方法。
baum-welch算法
baum-welch算法又称 前向-后向算法,由baum和welch,算法的本质其实就是用EM算法去估计P(O|λ)P(O|λ)的概率分布对应隐马尔可夫模型的参数。
确定完全数据的对数似然函数
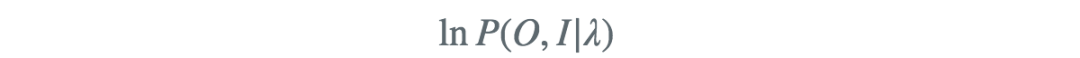
E步,求Q函数
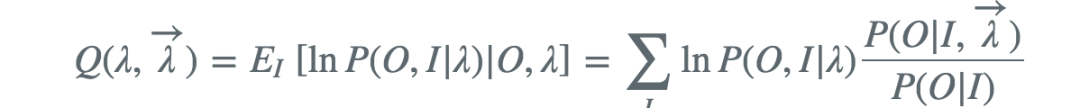
去掉对λ而言的常数因子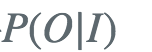

M步
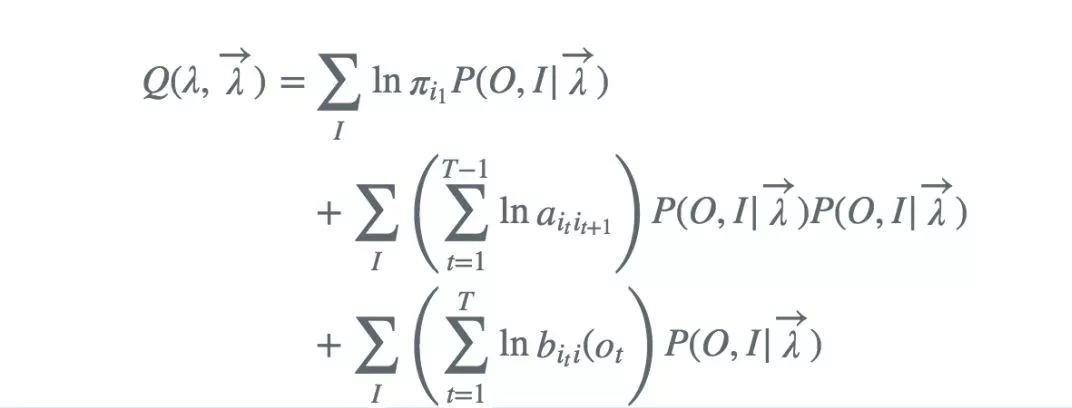
注意到![]() 满足约束条件 ,利用拉格朗日乘子法
满足约束条件 ,利用拉格朗日乘子法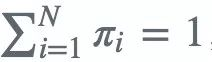 ,对其求偏导并令结果为0,得
,对其求偏导并令结果为0,得
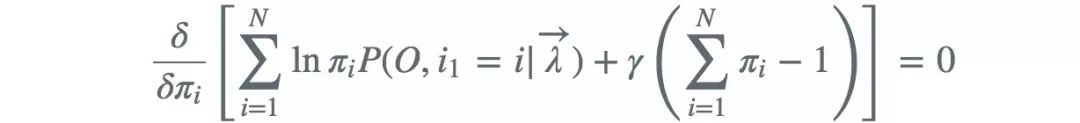

对i求和得到γ
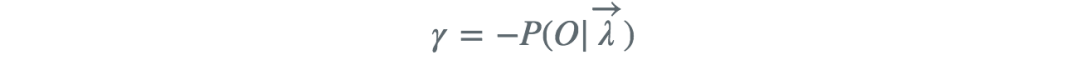
代入得
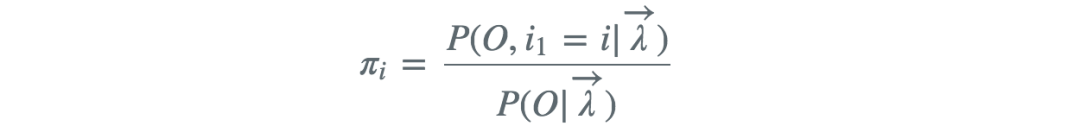
类似的求出
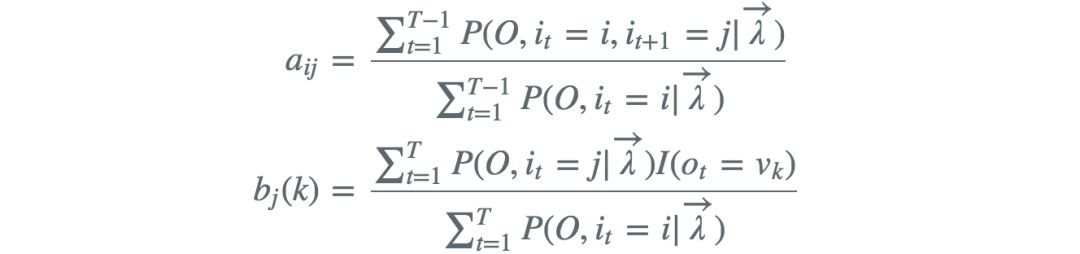
以上式子还可以写成
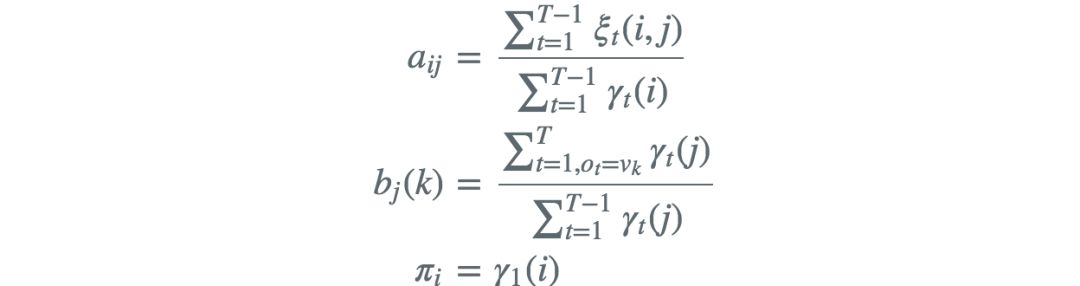
预测问题
近似算法
近似算法实际是一种贪心的方法,在每一步选择概率最大的状态值作为结果,但这样得到的结果有可能不是最佳的预测结果,但是近似算法的计算量非常的小。
维特比算法
维特比算法其实用了动态规划的方法求解HMM的解码问题。但在小的篇幅中很难把动态规划讲得浅显易懂。因此有兴趣的朋友可以去《数学之美》一书中去了解维特比算法。
资料来源:
《统计学习方法》 李航
以及网上各位大佬的博文




 本文介绍了隐马尔可夫模型(HMM),包括其历史背景、基本原理及在语言处理中的应用。HMM是一种概率模型,用于处理序列数据,如语音识别和词性标注。文章详细解释了HMM的组成部分,包括状态序列、观测序列、状态转移矩阵等,并讨论了概率计算、学习和预测三个基本问题。
本文介绍了隐马尔可夫模型(HMM),包括其历史背景、基本原理及在语言处理中的应用。HMM是一种概率模型,用于处理序列数据,如语音识别和词性标注。文章详细解释了HMM的组成部分,包括状态序列、观测序列、状态转移矩阵等,并讨论了概率计算、学习和预测三个基本问题。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








