Regression
第一步:找模型
(1)线性模型:y=b+∑wixiy=b+{\sum}w_ix_iy=b+∑wixi
xxx:特征。
xix_ixi:特征xxx的一个属性值。
wiw_iwi:(weight)对应xix_ixi的一个权值。
bbb:(bias)
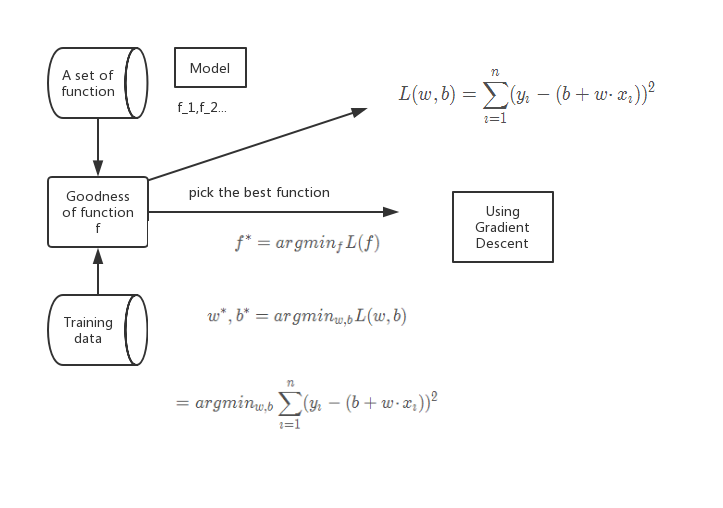
第二步:损失函数
input: function.
output:how bad the function is.
L:L:L:均方误差。
L(w,b)=∑i=1n(yi−(b+w⋅xi))2L(w,b)=\sum^n_{i=1}(y_i-(b+w·x_i))^2L(w,b)=i=1∑n(yi−(b+w⋅xi))2
f∗=argminfL(f)f^*=argmin_fL(f)f∗=argminfL(f)
w∗,b∗=argminw,bL(w,b)w^*,b^*=argmin_{w,b}L(w,b)w∗,b∗=argminw,bL(w,b)
=argminw,b∑i=1n(yi−(b+w⋅xi))2=argmin_{w,b}\sum^n_{i=1}(y_i-(b+w·x_i))^2=argminw,bi=1∑n(yi−(b+w⋅xi))2
第三步:梯度下降
损失函数只有一个参数www:
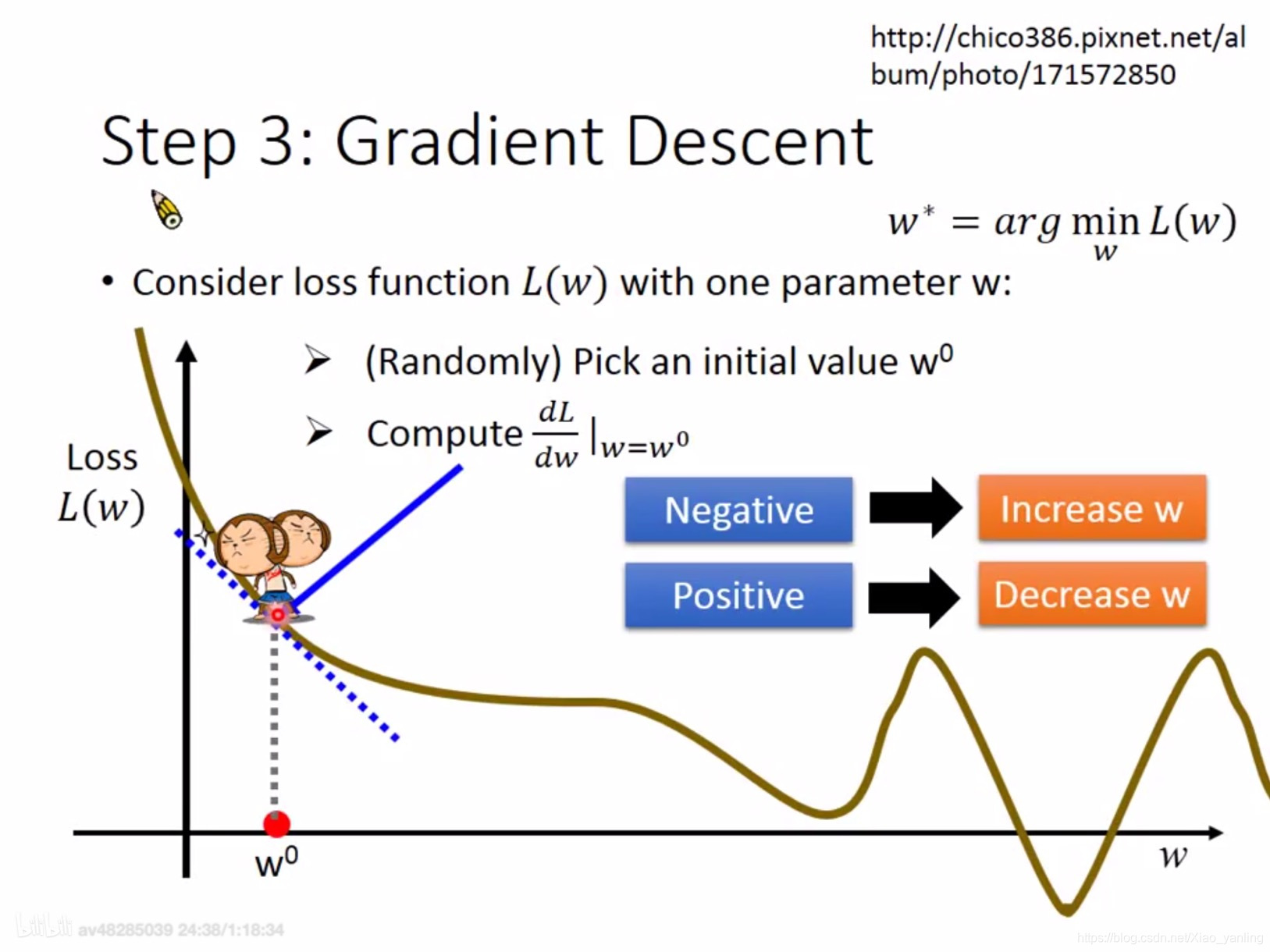
w0w^0w0:随机设
w1=w0−ηdLdw∣w=w0w^1=w^0-{\eta}\frac{dL}{dw}|w=w^0w1=w0−ηdwdL∣w=w0
w2=w0−ηdLdw∣w=w1w^2=w^0-{\eta}\frac{dL}{dw}|w=w^1w2=w0−ηdwdL∣w=w1
.........
η\etaη:学习率或步长。
多个参数时,同理分别更新。
Gradient:∇L=[∂L∂w,∂L∂b,...]T{\nabla}L=[\frac{{\partial}L}{{\partial}w},\frac{{\partial}L}{{\partial}b},...]^T∇L=[∂w∂L,∂b∂L,...]T
过拟合(overfitting):在训练时效果很好,但在测试时效果不好。
Regularization:
L(w,b)=∑i=1n(yi−(b+w⋅xi))2+λ∑(wi)2L(w,b)=\sum^n_{i=1}(y_i-(b+w·x_i))^2+\lambda\sum(w_i)^2L(w,b)=i=1∑n(yi−(b+w⋅xi))2+λ∑(wi)2
当wiw_iwi越小时,函数比较平滑,比较好,但不能过于平滑。(原因:噪声的影响比较小)b和平滑程度无关。




















 1163
1163

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








