#ifndef __BSTREE_H__
#define __BSTREE_H__
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef int DataType;
typedef struct BSTreeNode
{
struct BSTreeNode* _left;
struct BSTreeNode* _right;
DataType _data;
} BSTreeNode;
BSTreeNode* BuyBSTreeNode ( DataType x) ;
int BSTreeInsert ( BSTreeNode* * pptree, DataType x) ;
int BSTreeRemove ( BSTreeNode* * pptree, DataType x) ;
const BSTreeNode* BSTreeFind ( BSTreeNode* ptree, DataType x) ;
void BSTreeInOrder ( BSTreeNode* ptree) ;
void BSTreeDestory ( BSTreeNode* ptree) ;
int BSTreeInsertR ( BSTreeNode* * pptree, DataType x) ;
int BSTreeRemoveR ( BSTreeNode* * pptree, DataType x) ;
const BSTreeNode* BSTreeFindR ( BSTreeNode* ptree, DataType x) ;
#endif __BSTREE_H__
#define _CRT_SECURE_NO_WARNINGS 1
#include "BSTree.h"
BSTreeNode* BuyBSTreeNode ( DataType x)
{
BSTreeNode* node = ( BSTreeNode* ) malloc ( sizeof ( BSTreeNode) ) ;
assert ( node) ;
node-> _data = x;
node-> _left = NULL ;
node-> _right = NULL ;
return node;
}
int BSTreeInsert ( BSTreeNode* * pptree, DataType x)
{
if ( * pptree == NULL )
{
* pptree = BuyBSTreeNode ( x) ;
return 1 ;
}
BSTreeNode* prev = * pptree;
BSTreeNode* cur = * pptree;
while ( cur)
{
prev = cur;
if ( cur-> _data > x)
{
cur = cur-> _left;
}
else if ( cur-> _data < x)
{
cur = cur-> _right;
}
else
{
return 0 ;
}
}
if ( prev-> _data > x)
{
prev-> _left = BuyBSTreeNode ( x) ;
}
else if ( prev-> _data < x)
{
prev-> _right = BuyBSTreeNode ( x) ;
}
return 1 ;
}
int BSTreeRemove ( BSTreeNode* * pptree, DataType x)
{
if ( * pptree == NULL )
{
return 0 ;
}
BSTreeNode* cur = * pptree;
BSTreeNode* parent = * pptree;
while ( cur)
{
if ( cur-> _data > x)
{
parent = cur;
cur = cur-> _left;
}
else if ( cur-> _data < x)
{
parent = cur;
cur = cur-> _right;
}
else
{
if ( cur-> _left == NULL )
{
if ( cur == * pptree)
{
* pptree = cur-> _right;
}
else
{
if ( parent-> _left == cur)
{
parent-> _left = cur-> _right;
}
else
{
parent-> _right = cur-> _right;
}
}
free ( cur) ;
}
else if ( cur-> _right == NULL )
{
if ( cur == * pptree)
{
* pptree = cur-> _left;
}
else
{
if ( parent-> _left == cur)
{
parent-> _left = cur-> _left;
}
else
{
parent-> _right = cur-> _left;
}
}
free ( cur) ;
}
else
{
parent = cur;
BSTreeNode* subleft = cur-> _right;
while ( subleft-> _left)
{
parent = subleft;
subleft = subleft-> _left;
}
cur-> _data = subleft-> _data;
if ( parent-> _left == subleft)
{
parent-> _left = subleft-> _right;
}
else
{
parent-> _right = subleft-> _right;
}
free ( subleft) ;
subleft = NULL ;
}
return 1 ;
}
}
return 0 ;
}
const BSTreeNode* BSTreeFind ( BSTreeNode* ptree, DataType x)
{
if ( ptree == NULL )
{
return NULL ;
}
BSTreeNode* cur = ptree;
while ( cur)
{
if ( cur-> _data > x)
{
cur = cur-> _left;
}
else if ( cur-> _data < x)
{
cur = cur-> _right;
}
else
{
return cur;
}
}
return NULL ;
}
void BSTreeInOrder ( BSTreeNode* ptree)
{
if ( ptree == NULL )
{
return ;
}
BSTreeInOrder ( ptree-> _left) ;
printf ( "%d " , ptree-> _data) ;
BSTreeInOrder ( ptree-> _right) ;
}
void BSTreeDestory ( BSTreeNode* ptree)
{
if ( ptree == NULL )
{
return ;
}
BSTreeDestory ( ptree-> _left) ;
BSTreeDestory ( ptree-> _right) ;
free ( ptree) ;
}
int BSTreeInsertR ( BSTreeNode* * pptree, DataType x)
{
if ( * pptree == NULL )
{
* pptree = BuyBSTreeNode ( x) ;
return 1 ;
}
if ( ( * pptree) -> _data > x)
{
return BSTreeInsertR ( & ( * pptree) -> _left, x) ;
}
else if ( ( * pptree) -> _data < x)
{
return BSTreeInsertR ( & ( * pptree) -> _right, x) ;
}
else
{
return 0 ;
}
}
int BSTreeRemoveR ( BSTreeNode* * pptree, DataType x)
{
if ( * pptree == NULL )
{
return 0 ;
}
if ( ( * pptree) -> _data > x)
{
return BSTreeRemoveR ( & ( * pptree) -> _left, x) ;
}
else if ( ( * pptree) -> _data < x)
{
return BSTreeRemoveR ( & ( * pptree) -> _right, x) ;
}
else
{
if ( ( * pptree) -> _left == NULL )
{
* pptree = ( * pptree) -> _right;
return 1 ;
}
else if ( ( * pptree) -> _right == NULL )
{
* pptree = ( * pptree) -> _left;
return 1 ;
}
else
{
BSTreeNode* subleft = ( * pptree) -> _right;
while ( subleft-> _left)
{
subleft = subleft-> _left;
}
( * pptree) -> _data = subleft-> _data;
return BSTreeRemoveR ( & ( * pptree) -> _right, subleft-> _data) ;
}
}
}
const BSTreeNode* BSTreeFindR ( BSTreeNode* ptree, DataType x)
{
if ( ptree == NULL )
{
return NULL ;
}
if ( ptree-> _data > x)
{
return BSTreeFindR ( ptree-> _left, x) ;
}
else if ( ptree-> _data < x)
{
return BSTreeFindR ( ptree-> _right, x) ;
}
else
{
return ptree;
}
}
#define _CRT_SECURE_NO_WARNINGS 1
#include "BSTree.h"
int main ( )
{
BSTreeNode* tree = NULL ;
int a[ ] = { 5 , 3 , 4 , 1 , 7 , 8 , 2 , 6 , 0 , 9 } ;
for ( int i = 0 ; i < sizeof ( a) / sizeof ( a[ 0 ] ) ; ++ i)
{
BSTreeInsertR ( & tree, a[ i] ) ;
}
BSTreeInOrder ( tree) ;
printf ( "\n" ) ;
const BSTreeNode* node = BSTreeFindR ( tree, 2 ) ;
if ( node)
{
printf ( "找到了\n" ) ;
}
else
{
printf ( "没找到\n" ) ;
}
BSTreeRemove ( & tree, 2 ) ;
BSTreeRemove ( & tree, 5 ) ;
BSTreeRemove ( & tree, 7 ) ;
BSTreeRemove ( & tree, 8 ) ;
BSTreeInOrder ( tree) ;
printf ( "\n" ) ;
BSTreeDestory ( tree) ;
system ( "pause" ) ;
return 0 ;
}
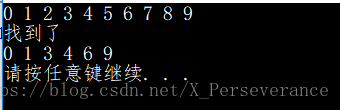
 二叉搜索树操作实现
二叉搜索树操作实现





 本文介绍了一种二叉搜索树的数据结构,并提供了插入、删除、查找等关键操作的具体实现。通过非递归和递归两种方式实现了这些功能,并通过一个示例程序展示了如何使用这些函数来构建和操作二叉搜索树。
本文介绍了一种二叉搜索树的数据结构,并提供了插入、删除、查找等关键操作的具体实现。通过非递归和递归两种方式实现了这些功能,并通过一个示例程序展示了如何使用这些函数来构建和操作二叉搜索树。
















 1540
1540

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








