（leetcode刷题）差分数组

最新推荐文章于 2025-01-30 11:42:42 发布

原创最新推荐文章于 2025-01-30 11:42:42 发布 · 197 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法

文章介绍了如何利用差分数组高效地处理数组区间操作，包括区间加法、单点操作的等价性，以及在拼车、航班预定统计、字母移位和花期内花的数目问题中的具体应用。

举例

考虑数组 a = [1,3,3,5,8]，对其中的相邻元素两两做差（右边减左边），得到数组[2,0,2,3]。然后在开头补上a[0]，得到差分数组

d = [1,2,0,2,3]

如果从左到右累加d中的元素，我们就还原回了a数组[1,3,3,5,8]。现在把连续数组a[1],a[2],a[3]都加上10，得到a' = [1,13,13,15,18]，再次两两作差，并在开头补上a'[0]，得到差分数组

d' = [1,12,0,2,-7]

对比d和d'，你会发现，对a中连续子数组的操作，可以转变为差分数组d中两个数的操作。

定义和性质

对于数组a，定义其差分数组为

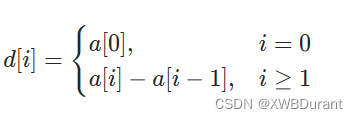
性质 1：从左到右累加 d 中的元素，可以得到数组 a。

性质 2：如下两个操作是等价的。

区间操作：把 a 的子数组a[i],a[i+1],⋯,a[j] 都加上 x。
单点操作：把d[i] 增加 x，把 [+1]d[j+1] 减少 x。特别地，如果 j+1=n，则只需把 [d[i] 增加 x。（n 为数组 a 的长度）

利用性质 2，我们只需要 (1)O(1) 的时间就可以完成数组 a 上的区间操作。最后利用性质 1 从差分数组复原出数组 a。

代码模板

// 你有一个长为 n 的数组 a，一开始所有元素均为 0。
// 给定一些区间操作，其中 queries[i] = [left, right, x]，
// 你需要把子数组 a[left], a[left+1], ... a[right] 都加上 x。
// 返回所有操作执行完后的数组 a。
vector<int> solve(int n, vector<vector<int>> queries) {
    vector<int> diff(n); // 差分数组
    for (auto &q: queries) {
        int left = q[0], right = q[1], x = q[2];
        diff[left] += x;
        if (right + 1 < n) {
            diff[right + 1] -= x;
        }
    }
    for (int i = 1; i < n; i++) {
        diff[i] += diff[i - 1]; // 直接在差分数组上复原数组 a
    }
    return diff;
}

lc1094 拼车

车上最初有 capacity 个空座位。车只能向一个方向行驶（也就是说，不允许掉头或改变方向）

给定整数 capacity 和一个数组 trips , trip[i] = [numPassengersi, fromi, toi] 表示第 i 次旅行有 numPassengersi 乘客，接他们和放他们的位置分别是 fromi 和 toi 。这些位置是从汽车的初始位置向东的公里数。

当且仅当你可以在所有给定的行程中接送所有乘客时，返回 true，否则请返回 false。

class Solution {
public:
    bool carPooling(vector<vector<int>>& trips, int capacity) {
        int dist[1001]{};
        for(auto &t : trips) {
            int num = t[0], from = t[1], to = t[2];
            dist[from] +=num;
            dist[to] -=num;
        }
        int s = 0;
        for(int v : dist) {
            s+=v;
            if(s>capacity) {
                return false;
            }
        }
        return true;
    }
};

lc1109 航班预定统计

这里有 n 个航班，它们分别从 1 到 n 进行编号。

有一份航班预订表 bookings ，表中第 i 条预订记录 bookings[i] = [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti （包含 firsti 和 lasti ）的 每个航班 上预订了 seatsi 个座位。

请你返回一个长度为 n 的数组 answer，里面的元素是每个航班预定的座位总数。

class Solution {
public:
    vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
        vector<int> ans(n,0);
        for(auto b : bookings) {
            int first = b[0],last = b[1], num = b[2];
            ans[first-1] +=num;
            if(last<n)
                ans[last] -=num;
        }
        for(int i =1;i<n;i++){
            ans[i] = ans[i-1] + ans[i];
        }
        return ans;
    }
};

lc2381. 字母移位II

给你一个小写英文字母组成的字符串 s 和一个二维整数数组 shifts ，其中 shifts[i] = [starti, endi, directioni] 。对于每个 i ，将 s 中从下标 starti 到下标 endi （两者都包含）所有字符都进行移位运算，如果 directioni = 1 将字符向后移位，如果 directioni = 0 将字符向前移位。

将一个字符向后移位的意思是将这个字符用字母表中 下一个 字母替换（字母表视为环绕的，所以 'z' 变成 'a'）。类似的，将一个字符向前移位的意思是将这个字符用字母表中 前一个 字母替换（字母表是环绕的，所以 'a' 变成 'z' ）。

请你返回对 s 进行所有移位操作以后得到的最终字符串。

class Solution {
public:
    string shiftingLetters(string s, vector<vector<int>>& shifts) {
        int size = s.size();
        vector<int> ans(size+1,0);
        for(auto s : shifts) {
            int left = s[0],right = s[1], n = s[2];
            if(n) {
                ans[left]++;
                ans[right+1]--;
            }else{
                ans[left]--;
                ans[right+1]++;
            }
        }
        for(int i =1;i<(size+1);i++){
            ans[i] += ans[i-1];
        }
        for(int i = 0 ;i<size;i++){
            s[i] = ((s[i] - 'a') + (ans[i])%26+26) %26+'a';
        }
        return s;
    }
};

lc2251 花期内花的数目

给你一个下标从 0 开始的二维整数数组 flowers ，其中 flowers[i] = [starti, endi] 表示第 i 朵花的花期从 starti 到 endi （都包含）。同时给你一个下标从 0 开始大小为 n 的整数数组 people ，people[i] 是第 i 个人来看花的时间。

请你返回一个大小为 n 的整数数组 answer ，其中 answer[i]是第 i 个人到达时在花期内花的数目。

差分优化前：

class Solution {
public:
    vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& people) {
        map<int,int > dist;
        for(auto f : flowers) {
            dist[f[0]]++;
            dist[f[1]+1]--;
        }
        vector<int> ans;
        int curr = 0;
        for(auto p : people) {
            auto it = dist.begin();
            curr=0;
            while(it!=dist.end()&&it->first<=p){
                curr+=it->second;
                it++;
            }
            ans.push_back(curr);
        }
        return ans;
    }
};

class Solution {
public:
    vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& people) {
        map<int,int > dist;
        for(auto f : flowers) {
            dist[f[0]]++;
            dist[f[1]+1]--;
        }
        int m = people.size();
        vector<int> indices(m);
        iota(indices.begin(),indices.end(),0);
        sort(indices.begin(),indices.end(),[&](int a,int b){
            return people[a] < people[b];
        });

        vector<int> ans(m);
        int curr = 0;
        auto it = dist.begin();
        for(auto x : indices) {
            while(it!=dist.end()&&it->first<=people[x]){
                curr+=it->second;
                it++;
            }
            ans[x] = curr;
        }
        return ans;
    }
};