LeetCode刷题笔记 51. N皇后

题目描述

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

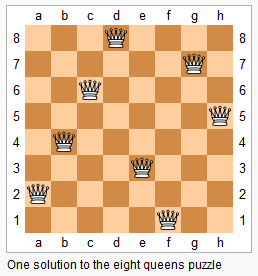
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例:
输入: 4
输出: [
[".Q…", // 解法 1
“…Q”,
“Q…”,
“…Q.”],

["…Q.", // 解法 2
“Q…”,
“…Q”,
“.Q…”]
]
解释: 4 皇后问题存在两个不同的解法。

Sample Code

backTrack() 里面 col[]维护行，left[]和right[]维护两个斜边，列（或行）由循环维护

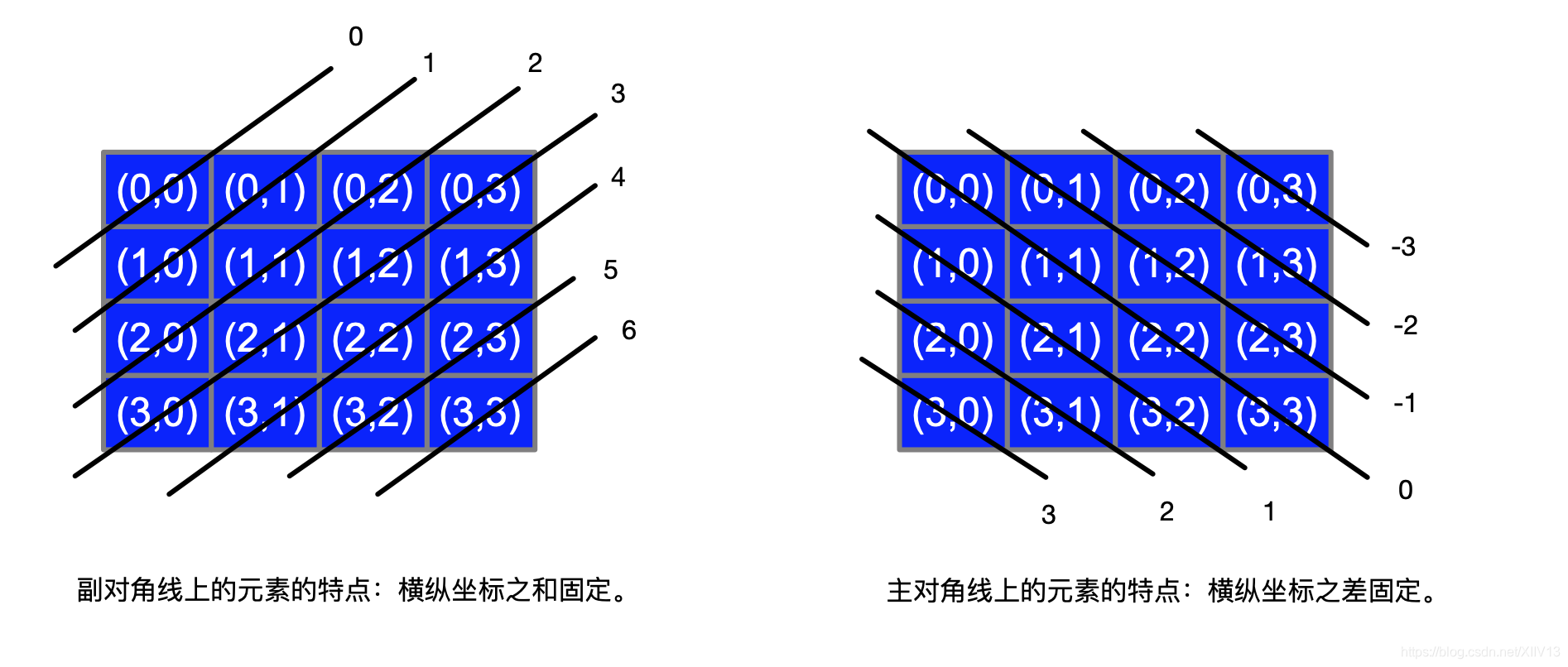
可以用二进制来表示，以节省空间

class Solution {
    int N;
    boolean[] col;
    boolean[] left;
    boolean[] right;
    List<List<String>> res = new ArrayList<>();

    public List<List<String>> solveNQueens(int n) {
        N = n;
        col = new boolean[n];
        left = new boolean[2*N-1];
        right = new boolean[2*N-1];
        char[][] board = new char[N][N];

        backTrack(board, 0);
        return res;
    }

    private void backTrack(char[][] board, int c) {
        if (c >= N) {
            List<String> list = new ArrayList<>();
            for (int i = 0; i < N; i++)
                list.add(new String(board[i]));
            res.add(list);
            return;
        }
        
        Arrays.fill(board[c], '.');
        for (int i = 0; i < N; i++) {
            if (!col[i] && !left[c + i] && !right[N + c - i - 1]) {   // 三个都要为false
                board[c][i] = 'Q';
                col[i] = true;
                left[c + i] = true;
                right[N + c - i - 1] = true;

                backTrack(board, c + 1);

                board[c][i] = '.';
                col[i] = false;
                left[c + i] = false;
                right[N + c - i - 1] = false;
            }
        }
    }
}

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/n-queens
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。