加密技术的爱恨情仇：当对称加密邂逅非对称加密

加密技术的爱恨情仇：当对称加密邂逅非对称加密

先思考

• 加密算法有哪些类型，对称加密和非对称加密分别有什么特点？
• 消息摘要与数字签名是什么技术？
• 各种加密算法应该如何配合使用？

---

—— 2025 年 10 月 23 号 乙巳蛇年九月初三 霜降

扫码关注微信公众号   了解最新最全文章

1 对称加密

  对称加密是指使用同一个密钥来进行数据的加解密，也称为私钥加密或共享密钥加密。通信双方在加密通信之前，必须安全地共享同一个密钥。

1.1 核心特点

• 效率高，速度快：加密算法相对简单，计算开销小，因此适合加密大数据。
• 密钥分发和管理困难：通信双方必须安全地交换并保管同一个密钥。在拥有 N 个用户的网络中，需要管理 N (N - 1) / 2 个密钥，密钥管理复杂度高。
• 无法验证真伪和抗抵赖：因为密钥是共享的，所以接收方虽然可以解密消息，但无法从消息本身确认发送方的身份。

1.2 常见算法

• DES、3DES：DES 密钥长度为 56 位，3DES 为前者的升级版，密钥长度为 168 位（两个 56 位的密钥，做三次加密，也称为三重 DES），安全性高于前者。
• RC-5、IDEA：前者密钥长度可变，后者密钥长度为 128 位。
• AES：密钥长度有 128、192 和 256 位，逐步代替了 DES，成为目前最主流和最安全的对称加密算法。

1.3 适用场景

• 大量数据加密：适合加密大量数据，如文件内容、会话数据流等。
• 数据存储加密：加密本地硬盘、数据库字段等。
• 网络数据加密：用于保护传输在网络上的数据。

2 非对称加密

  非对称加密是指使用一对数学上关联的被称为公钥和私钥的密钥来进行数据的加解密。公钥可以共享给通信方，私钥必须严格保密，也称为公钥加密。

2.1 核心特点

• 密钥成对出现：密钥分为公钥和私钥，公私钥之间不能相互推导。
• 公钥对外公开，私钥只能持有者保存。
• 支持数字签名：发送方可用自己的私钥对信息生成签名，任何接收方都可以用发送方公开的公钥验证签名，从而实现身份认证，具有抗抵赖性。
• 不存在密钥分发难题：任何用户都可以使用公钥公开方的公钥加密数据，但只有对应私钥的接收方才能解密。
• 效率低，速度慢：加密算法比对称加密复杂，计算开销也比对称加密大，因此不适合对大数据进行加密。

2.2 常见算法

• RSA：密钥长度为 1024、2048 位，是最经典、应用最广泛的非对称加密算法，即可用于通信加密，也可用于数字签名。
• ECC：椭圆曲线加密算法，在同等安全强度下，其密钥长度短于 RSA（如 256 位 ECC 约等于 3072 位 RSA），计算快，资源消耗少。
• Elgamall、DES、Diffie-Hellman 等也属于非对称加密算法。

2.3 适用场景

• 数字签名：可用于 SSL/TLS 证书、代码签名、电子合同签名、区块链交易验证等。
• 加密小量关键数据：可用于加密小量的极为关键的数据。
• 安全交换对称密钥：可用于在通信双方之间交换对称密钥。

3 国产加密算法

• SM1：对称加密算法，密钥长度和分组长度都为 128 位，主要用于电子政务、电子商务及相关领域。
• SM2：非对称加密算法，用于公钥加密算法、对称密钥交换、数字签名等，且国家标准推荐使用素数域 256 位椭圆曲线。
• SM3：杂凑算法，杂凑值长度为 256 位，适用于商用密码应用中的数字签名和验证。
• SM4：对称加密算法，密钥长度和分组长度都为 128 位，适用于无线局域网产品。
• SM9：标识密码算法，不需要申请数字证书，适用于互联网应用的各种新兴应用的安全保障。

4 消息摘要算法

  消息摘要算法通常称为哈希函数或散列函数，加密算法是为了 保密，而摘要算法是为了保证信息完整性，防篡改。

  常见的消息摘要算法有 MD5、SHA 等，且市场上广泛使用的 MD5 、SHA 摘要算法的散列值分别为 128 位和 160 位，因为 SHA 的常用密钥长度较长，故其安全性也高于 MD5。

5 数字签名技术

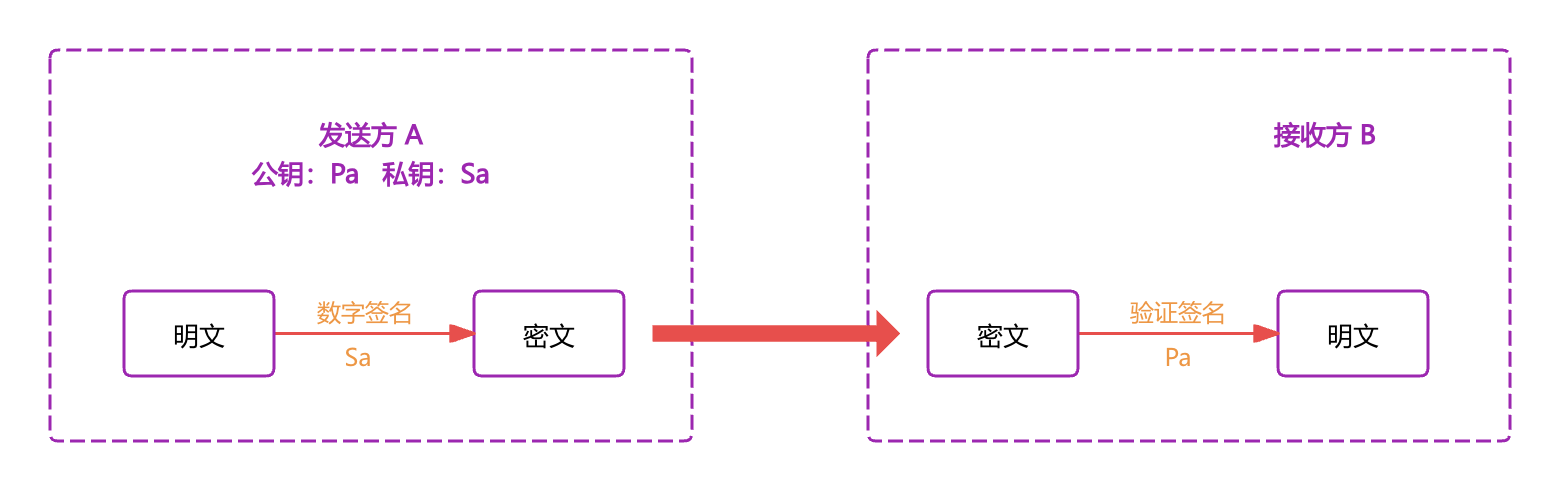
  数字签名技术是指基于非对称加密的密码学技术，它允许信息的发送者生成一个只有自己才能产生的签名，附加在原始信息上，任何接收者都可以使用公开的密钥来验证改签名的真伪，签名无法伪造，所以数字签名技术主要实现目的：

• 身份认证：证明信息缺失来自该发送者。
• 抗抵赖性：发送者事后无法抵赖自己签发了该信息。

  同时，为了防止签名被重复使用，在生成数字签名时可加入时间戳信息，进一步加强签名的有效性。

6 加解密技术综合应用

  假设存在这样一个场景：发送方 A 要向接收方 B 发送一份邮件，该邮件内容涉密，内容可达 1GB，且发送者不可抵赖，同时，若邮件被第三方截获，则第三方无法篡改邮件内容。根据场景要求进而分析得知：

• 邮件内容涉密，则说明该邮件需要加密传输；
• 内容可达 1GB，则说明要加密数据量过大，需要采用对称加密；
• 若要采用对称加密，则需要在双方之间安全传输密钥，那么就需要使用非对称加密；
• 发送者不可抵赖，则说明需要进行数字签名；
• 第三方截获邮件后不可篡改，则说明需要生成消息摘要；

  通过以上分析，则其设计图如下所示：

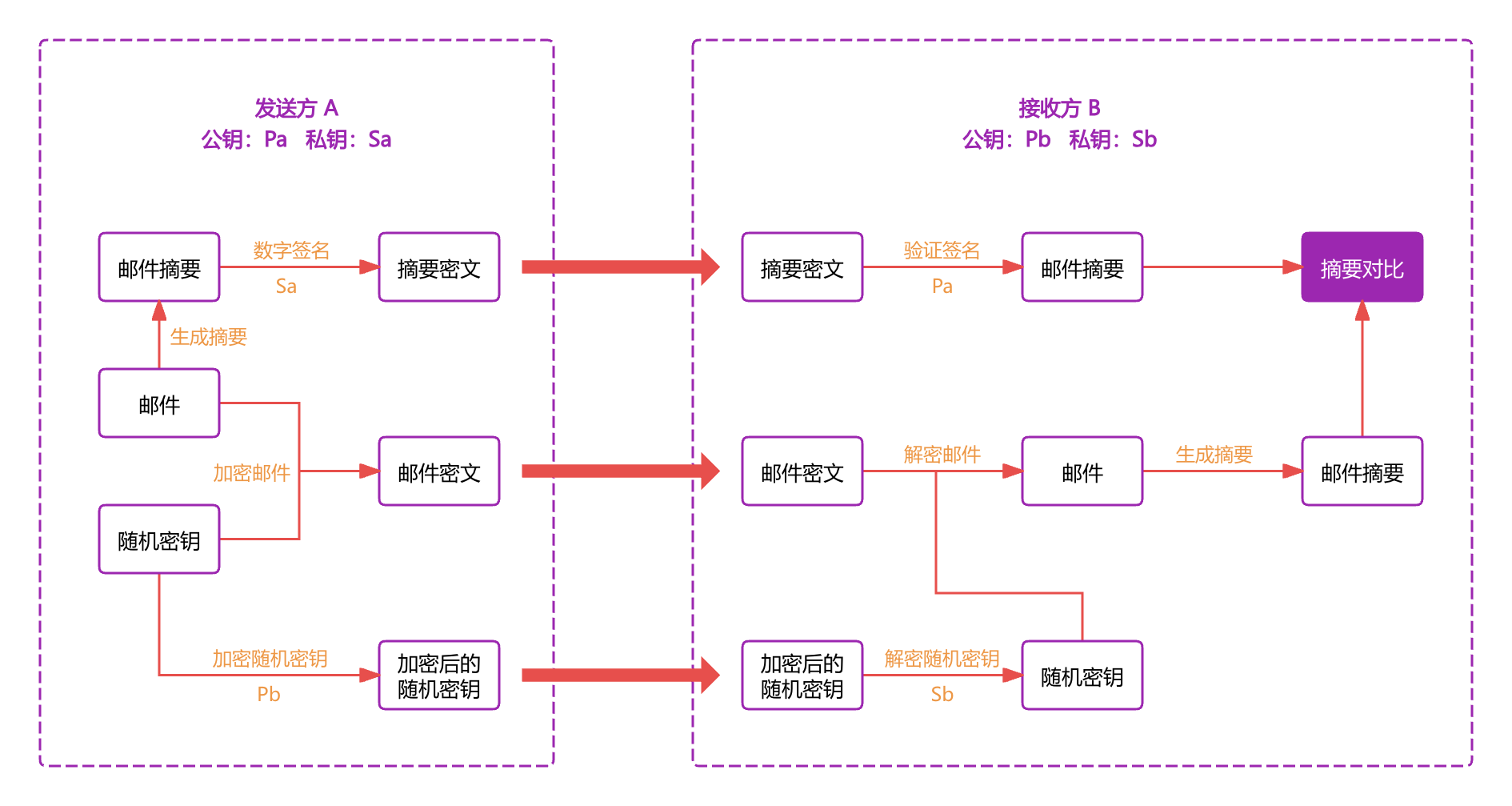
  发送方 A 需要生成一个随机密钥，用于通过对称加密来加密邮件内容；同时需要生成一对非对称加密的公私钥，记为 Pa 和 Sa，这里的非对称加密用作数字签名，发送方签名，接收方验签，所以发送方 A 需要通过安全渠道将自己的公钥 Pa 共享给接收方 B 。

  接收方 B 与发送方 A 之间需要安全传输随机密钥，因为随机密钥由发送方生成，属于小而极关键的数据，且由于接收方作为解密方，所以接收方 B 也需要生成一对公私钥，记为 Pb 和 Sb，同时需要将自己的公钥 Pb 通过安全渠道共享给发送方 A。

  同时，双方需要确定用于加解密或摘要的具体算法类型，当然，这个可以是动态的，只需要二者在进行同一个或同一类操作（如发送方加密，接收方解密；生成消息摘要）时，使用的是同一个算法即可。

发送方 A：

• 1、发送方使用消息摘要算法生成邮件摘要，并使用自己的私钥 Sa 对邮件摘要进行签名得到摘要密文；
• 2、发送方生成随机密钥，并使用对称加密算法对邮件内容进行加密得到邮件密文；
• 3、发送方使用接收方的公钥 Pb 对随机密钥进行加密得到加密后的随机密钥；
• 4、发送方将摘要密文、邮件密文和加密后的随机密钥共同发送给接收方；

接收方 B：

• 1、接收方使用发送方的公钥 Pa 对摘要密文进行验签，若验签通过则说明该邮件未被截获有效，得到发送方的邮件摘要；
• 2、接收方使用自己的私钥 Sb 对加密后的随机密钥进行解密，得到发送方生成的随机密钥；
• 3、接收方使用随机密钥解密邮件密文得到邮件内容；
• 4、接收方根据邮件内容使用和发送方相同的摘要算法生成邮件摘要；
• 5、接收方对比发送方的邮件摘要和自己生成的邮件摘要，若一致则说明邮件内容未被篡改，反之亦然；

  这样设计的精髓在于：

• 用对称加密处理大数据的通信，保证了高效性；
• 用非对称加密解决了对称加密最重要的密钥分发问题；
• 用消息摘要确保数据不被篡改；
• 用非对称加密实现数字签名，可进行身份认证以防抵赖；

扫码关注微信公众号   了解最新最全文章