文章目录
6. 第六章 逻辑回归(Logistic Regression)
6.1 分类(Classification)
标签 y ∈ { 0 , 1 } y \in \{ 0,1\} y∈{0,1},其中 0 0 0:表示负类(Negative class); 1 1 1:表示正类(Positive class)。
0 , 1 0,1 0,1的定义没有明确的规定,但倾向于 1 1 1表示我们要找的东西, 0 0 0表示没有。
问题:直接用单纯的线性回归,往往不能得到一个很好的假设,因此不推荐直接将线性回归应用于分类问题。
原先的 h θ ( x ) {h_\theta }(x) hθ(x)取值可以大于1或者小于0,但是逻辑回归要求 0 ≤ h θ ( x ) ≤ 1 0 \le {h_\theta }(x) \le 1 0≤hθ(x)≤1。
注意:逻辑回归虽然名字带有回归,而实际上却是解决分类问题。
6.2 逻辑回归:假设陈述
目标:想要 h θ ( x ) {h_\theta }(x) hθ(x)取值满足 0 ≤ h θ ( x ) ≤ 1 0 \le {h_\theta }(x) \le 1 0≤hθ(x)≤1。
令 h θ ( x ) = g ( θ T x ) {h_\theta }(x) = g({\theta ^T}x) hθ(x)=g(θTx),其中 g ( z ) = 1 1 + e − z g(z) = {1 \over {1 + {e^{ - z}}}} g(z)=1+e−z1,即sigmod函数
h θ ( x ) = 1 1 + e − θ T x {h_\theta }(x) = {1 \over {1 + {e^{ - {\theta ^T}x}}}} hθ(x)=1+e−θTx1
假设输出解释: h θ ( x ) {h_\theta }(x) hθ(x)是在输入 x x x的前提下的 y = 1 y = 1 y=1的可能性,即 P ( y = 1 ∣ x ; θ ) = h θ ( x ) P(y = 1|x;\theta ) = {h_\theta }(x) P(y=1∣x;θ)=hθ(x),同时满足 P ( y = 0 ∣ x ; θ ) = 1 − P ( y = 0 ∣ x ; θ ) = 1 − h θ ( x ) P(y = 0|x;\theta ) = 1 - P(y = 0|x;\theta ) = 1 - {h_\theta }(x) P(y=0∣x;θ)=1−P(y=0∣x;θ)=1−hθ(x), P ( y = 1 ∣ x ; θ ) + P ( y = 0 ∣ x ; θ ) = 1 P(y = 1|x;\theta ) + P(y = 0|x;\theta ) = 1 P(y=1∣x;θ)+P(y=0∣x;θ)=1
6.3 决策边界(Decision Boundary)
- 预测 y = 1 y = 1 y=1,如果 h θ ( x ) ≥ 0.5 {h_\theta }(x) \ge 0.5 hθ(x)≥0.5
- 预测 y = 0 y = 0 y=0,如果 h θ ( x ) < 0.5 {h_\theta }(x) < 0.5 hθ(x)<0.5
g ( z ) ≥ 0.5 ⇒ z ≥ 0 ⇒ θ T x ≥ 0 g(z) \ge 0.5 \Rightarrow z \ge 0 \Rightarrow {\theta ^T}x \ge 0 g(z)≥0.5⇒z≥0⇒θTx≥0同理 g ( z ) < 0.5 ⇒ z < 0 ⇒ θ T x < 0 g(z) < 0.5 \Rightarrow z < 0 \Rightarrow {\theta ^T}x < 0 g(z)<0.5⇒z<0⇒θTx<0,所以 θ T x = 0 {\theta ^T}x = 0 θTx=0两侧分为两种情况,这个超平面是决策边界。决策边界是假设本身及其参数的属性。
同时通过特征的各种非线性组合也可以拟合出很复杂的决策边界,如: x 1 x 2 , x i 2 {x_1}{x_2},{x_i}^2 x1x2,xi2等。
6.4 损失函数(Cost Function)
如何拟合出逻辑回归的参数 θ \theta θ?
训练集: { ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , . . . , ( x ( m ) , y ( m ) ) } \{ ({x^{(1)}},{y^{(1)}}),({x^{(2)}},{y^{(2)}}),...,({x^{(m)}},{y^{(m)}})\} {(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m))}, m m m个训练样本, x ∈ R n + 1 , x 0 = 1 , y ∈ { 0 , 1 } x \in {R^{n + 1}},{x_0} = 1,y \in \{ 0,1\} x∈Rn+1,x0=1,y∈{0,1}。
假设函数: h θ ( x ) = 1 1 + e − θ T x {h_\theta }(x) = {1 \over {1 + {e^{ - {\theta ^T}x}}}} hθ(x)=1+e−θTx1
如何选择参数 θ \theta θ?
回顾线性回归: J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta ) = {1 \over {2m}}\sum\limits_{i = 1}^m {{{({h_\theta }({x^{(i)}}) - {y^{(i)}})}^2}} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2, cos t ( h θ ( x ) , y ) = 1 2 ( h θ ( x ( i ) ) − y ( i ) ) 2 \cos t({h_\theta }(x),y) = {1 \over 2}{({h_\theta }({x^{(i)}}) - {y^{(i)}})^2} cost(hθ(x),y)=21(hθ(x(i))−y(i))2。
如果直接采用这个作为逻辑回归的代价函数,会是非凸函数,导致优化困难,因此引入新的代价函数。
逻辑回归的损失函数: cos t ( h θ ( x ) , y ) = { − log ( 1 − h θ ( x ) ) , y = = 0 − log ( h θ ( x ) ) , y = = 1 \cos t({h_\theta }(x),y) = \{ _{ - \log (1 - {h_\theta }(x)),y = = 0}^{ - \log ({h_\theta }(x)),y = = 1} cost(hθ(x),y)={−log(1−hθ(x)),y==0−log(hθ(x)),y==1,因此如果 y = 1 {y = 1} y=1并且 h θ ( x ) = 1 {h_\theta }(x){\rm{ = }}1 hθ(x)=1则 cos t = 0 \cos t = 0 cost=0,如果 y = 1 {y = 1} y=1并且 h θ ( x ) = 0 {h_\theta }(x){\rm{ = }}0 hθ(x)=0则 cos t = + ∞ \cos t = {\rm{ + }}\infty cost=+∞。
直觉:如果我们的输出 h θ ( x ) {h_\theta }(x) hθ(x)不一致时,我们的学习算法将会有一个很大的处罚。
这个代价函数是一个凸优化问题。
6.5 简化代价函数与梯度下降
逻辑回归的损失函数: cos t ( h θ ( x ) , y ) = { − log ( 1 − h θ ( x ) ) , y = = 0 − log ( h θ ( x ) ) , y = = 1 \cos t({h_\theta }(x),y) = \{ _{ - \log (1 - {h_\theta }(x)),y = = 0}^{ - \log ({h_\theta }(x)),y = = 1} cost(hθ(x),y)={−log(1−hθ(x)),y==0−log(hθ(x)),y==1,注意到 y = 0 o r y = 1 {\rm{y = }}0{\rm{ory = }}1 y=0ory=1,因此合并两种情况得: cos t ( h θ ( x ) , y ) = − y log ( h θ ( x ) ) − ( 1 − y ) log ( 1 − h θ ( x ) ) \cos t({h_\theta }(x),y){\rm{ = - y}}\log ({h_\theta }(x)) - (1 - y)\log (1 - {h_\theta }(x)) cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))。
cos t ( h θ ( x ) , y ) = 1 m ∑ i = 1 m cos t ( h θ ( x ( i ) ) − y ( i ) ) = − 1 m [ Σ i = 1 m y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] \cos t({h_\theta }(x),y) = {1 \over m}\sum\limits_{i = 1}^m {\cos t} ({h_\theta }({x^{(i)}}) - {y^{(i)}}) = - {1 \over m}[\mathop \Sigma \limits_{i = 1}^m {{\rm{y}}^{(i)}}\log ({h_\theta }({x^{(i)}})) + (1 - {{\rm{y}}^{(i)}})\log (1 - {h_\theta }({x^{(i)}}))] cost(hθ(x),y)=m1i=1∑mcost(hθ(x(i))−y(i))=−m1[i=1Σmy(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
想要 m i n θ J ( θ ) \mathop {min}\limits_\theta J(\theta ) θminJ(θ)
θ j : = θ j − α ∂ ∂ θ j J ( θ ) {\theta _j}: = {\theta _j} - \alpha {\partial \over {\partial {\theta _j}}}J(\theta ) θj:=θj−α∂θj∂J(θ)
∂ ∂ θ j J ( θ ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) {\partial \over {\partial {\theta _j}}}J(\theta ) = {1 \over m}\sum\limits_{i = 1}^m {{{({h_\theta }({x^{(i)}}) - {y^{(i)}})}^{}}} x_j^{(i)} ∂θj∂J(θ)=m1i=1∑m(hθ(x(i))−y(i))xj(i)
θ j : = θ j − α ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) , {\theta _j}: = {\theta _j} - \alpha \sum\limits_{i = 1}^m {{{({h_\theta }({x^{(i)}}) - {y^{(i)}})}^{}}} x_j^{(i)}, θj:=θj−αi=1∑m(hθ(x(i))−y(i))xj(i), 1 m {1 \over m} m1并入 α \alpha α,注意:要同时更新所有的 θ j {\theta _j} θj
综上:与线性回归形式相同只是 h θ ( x ) {h_\theta }(x) hθ(x)不同。
逻辑回归同样可以进行特征缩放,使得梯度下降收敛速度更快。
6.6 高级优化方法
优化算法:
- 梯度下降法(常用,简单)
- 共轭梯度法(conjugate gradient)
- 拟牛顿法(BFGS)
- L-BFGS
高级优化算法的优点:
- 无需手动挑选学习率 α \alpha α
- 通常比梯度下降法更快
高级优化算法的缺点:
- 更复杂
6.7 多分类:一对多(one-vs-all)
标签: y ∈ { 0 , 1 , 2 , . . . } {\rm{y}} \in {\rm{\{ 0,1,2,}}...{\rm{\} }} y∈{0,1,2,...}
多分类转换为多个二分类 ⇒ \Rightarrow ⇒一对其他,如:一个三分类问题可以转化为三个二分类问题
one-vs-all:
- 对于每种类别 i i i分别训练逻辑回归分类器 h θ ( i ) ( x ) h_\theta ^{(i)}(x) hθ(i)(x)去预测 y = i y = i y=i的可能性
- 在一个新的输入 x x x上进行预测,挑选 h θ ( i ) ( x ) h_\theta ^{(i)}(x) hθ(i)(x)最大值作为该输入的类别,即 max i h θ ( i ) ( x ) \mathop {\max }\limits_i h_\theta ^{(i)}(x) imaxhθ(i)(x)
7. 第七章 正则化(Regularization)
7.1 过拟合问题(overfitting)
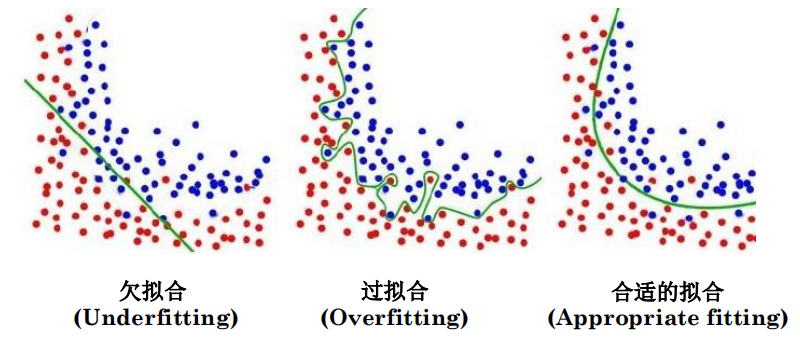
欠拟合:相较于数据而言,模型参数过少或者模型结构过于简单,以至于无法捕捉到数据中的规律的现象。高偏差(high bias)
过拟合:模型过于紧密或精确地匹配特定数据集,以致于无法良好地拟合其他数据或预测未来的观察结果的现象。高方差(high variance)
合适的拟合:模型能够恰当地拟合和捕捉到数据中规律的现象
过拟合:我们有很多特征,我们学习的超参数适合几乎所有的训练数据(代价函数约等于 0 0 0),但是无法泛化(generalize)到新的数据集上(测试集)。
泛化:指模型在新数据上的性能。新数据:未在训练数据集上出现过的样本
解决过拟合:
- 减少特征数量
- 人工选择保留哪些特征
- 模型选择算法
- 正则化
- 保留所有的特征,但是减少参数 θ j {\theta _j} θj的值
- 当我们有大量特征时表现好,每个特征对预测 y y y的值贡献一点
7.2 代价函数(cost function)
直觉:
θ 0 + θ 1 x + θ 2 x 2 {\theta _0} + {\theta _1}x + {\theta _2}{x^2} θ0+θ1x+θ2x2是一个好的拟合,而 θ 0 + θ 1 x + θ 2 x 2 + θ 3 x 3 + θ 4 x 4 {\theta _0} + {\theta _1}x + {\theta _2}{x^2} + {\theta _3}{x^3} + {\theta _4}{x^4} θ0+θ1x+θ2x2+θ3x3+θ4x4是一个过拟合
假设我们惩罚,使 θ 3 {\theta _3} θ3和 θ 4 {\theta _4} θ4很小,如: min θ 1 2 m ∑ i = 1 m cos t ( h θ ( x ( i ) ) − y ( i ) ) 2 + 100 θ 3 3 + 100 θ 4 4 \mathop {\min }\limits_\theta {1 \over {2m}}\sum\limits_{i = 1}^m {\cos t} {({h_\theta }({x^{(i)}}) - {y^{(i)}})^2} + 100\theta _3^3 + 100\theta _4^4 θmin2m1i=1∑mcost(hθ(x(i))−y(i))2+100θ33+100θ44,为了最小化这个值 θ 3 ≈ 0 , θ 4 ≈ 0 {\theta _3} \approx 0,{\theta _4} \approx 0 θ3≈0,θ4≈0,通过让 θ 3 {\theta _3} θ3和 θ 4 {\theta _4} θ4很小,这样得到一个更加简单地模型。
正则化:
参数 θ j {\theta _j} θj取小值的好处:更简单的假设(平滑);不易过拟合;减小噪声的影响。
由于我们并不知道去缩小哪些参数 θ \theta θ的值去正则化,因此加入 λ ∑ j = 1 n θ j 2 \lambda \sum\limits_{j = 1}^n {\theta _j^2} λj=1∑nθj2正则化项,让每个参数 θ \theta θ的值都小。
加入正则化项的代价函数: J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 J(\theta ) = {1 \over {2m}}\sum\limits_{i = 1}^m {} {({h_\theta }({x^{(i)}}) - {y^{(i)}})^2} + \lambda \sum\limits_{j = 1}^n {\theta _j^2} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2一般无 θ 0 {\theta _0} θ0,其中 λ \lambda λ表示正则化数。
如果$ λ \lambda λ设置过大会发生什么(如: λ = 1 0 10 \lambda =10^{10} λ=1010?
这样会导致所有参数都约等于 0 0 0,从而 h θ ( x ) = θ 0 {h_\theta }(x) = {\theta _0} hθ(x)=θ0,即用一条水平直线去拟合导致欠拟合。
7.3 正则化线性回归
- 梯度下降法
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 J(\theta ) = {1 \over {2m}}\sum\limits_{i = 1}^m {} {({h_\theta }({x^{(i)}}) - {y^{(i)}})^2} + \lambda \sum\limits_{j = 1}^n {\theta _j^2} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2
m i n θ J ( θ ) \mathop {min}\limits_\theta J(\theta ) θminJ(θ)
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) {\theta _0}: = {\theta _0} - \alpha {1 \over m}\sum\limits_{i = 1}^m {{{({h_\theta }({x^{(i)}}) - {y^{(i)}})}^{}}} x_0^{(i)} θ0:=θ0−αm1i=1∑m(hθ(x(i))−y(i))x0(i)
θ j : = θ j − α 1 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] ⇒ θ j : = θ j ( 1 − α λ m ) − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) {\theta _j}: = {\theta _j} - \alpha {1 \over m}[\sum\limits_{i = 1}^m {{{({h_\theta }({x^{(i)}}) - {y^{(i)}})}^{}}} x_j^{(i)} + {\lambda \over m}{\theta _j}] \Rightarrow {\theta _j}: = {\theta _j}(1 - \alpha {\lambda \over m}) - \alpha {1 \over m}\sum\limits_{i = 1}^m {{{({h_\theta }({x^{(i)}}) - {y^{(i)}})}^{}}} x_j^{(i)} θj:=θj−αm1[i=1∑m(hθ(x(i))−y(i))xj(i)+mλθj]⇒θj:=θj(1−αmλ)−αm1i=1∑m(hθ(x(i))−y(i))xj(i)
1 − α λ m 1 - \alpha {\lambda \over m} 1−αmλ是一个略小于 1 1 1的数,因为通常 α \alpha α较小, m m m较大。
- 标准方程
m i n θ J ( θ ) \mathop {min}\limits_\theta J(\theta ) θminJ(θ)
θ = ( X T X ) − 1 X T y ⇒ θ = ( X T X + λ I ( n + 1 ) × ( n + 1 ) ) − 1 X T y \theta = {({X^T}X)^{ - 1}}{X^T}y \Rightarrow \theta = {({X^T}X + \lambda {I_{(n + 1) \times (n + 1)}})^{ - 1}}{X^T}y θ=(XTX)−1XTy⇒θ=(XTX+λI(n+1)×(n+1))−1XTy
7.4 正则化逻辑回归
g ( ∗ ) {\rm{g}}( * ) g(∗)表示sigmod函数。
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) {\theta _0}: = {\theta _0} - \alpha {1 \over m}\sum\limits_{i = 1}^m {{{({h_\theta }({x^{(i)}}) - {y^{(i)}})}^{}}} x_0^{(i)} θ0:=θ0−αm1i=1∑m(hθ(x(i))−y(i))x0(i)
θ j : = θ j − α 1 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] {\theta _j}: = {\theta _j} - \alpha {1 \over m}[\sum\limits_{i = 1}^m {{{({h_\theta }({x^{(i)}}) - {y^{(i)}})}^{}}} x_j^{(i)} + {\lambda \over m}{\theta _j}] θj:=θj−αm1[i=1∑m(hθ(x(i))−y(i))xj(i)+mλθj]
其中 [ ] [] []里面是 ∂ ∂ θ j J ( θ ) {\partial \over {\partial {\theta _j}}}J(\theta ) ∂θj∂J(θ)。
8. 第八章 神经网络:表示(Neural Network:Representation)
8.1 非线性假设(Non-linear hypothesis)
之前的方法如果拟合比较复杂的数据集,可能要引入很多次的特征表示,比如有 x 1 , x 2 {x_1},{x_2} x1,x2两个特征,引入所有二次项有 3 3 3个,若有100个特征引入所有二次项有 n ( n − 1 ) 2 {{n(n - 1)} \over 2} 2n(n−1)个,会导致特征非常多。因此,当初始特征个数 n n n很大时,将这些高阶多项式项数都包含到特征中,会使得特征空间急剧膨胀。综上,当初始特征个数 n n n很大时,通过增加特征来建立非线性分类器并不是一个好做法。
计算机视觉任务中特征数就是非常巨大的,简单的逻辑回归难以解决这类问题。
而神经网络在处理学习复杂的非线性假设上有独特的优势,即使 n n n很大。
8.2 神经元和大脑
起源:算法尝试模仿大脑。
神经网络在80年代和90年代早期非常流行,在90年代后期流行度下降。
近来神经网络热度重新上升:已经在很多应用领域成为目前最先进的方法。
amazing:你能把几乎任何传感器接入到大脑中,大脑的学习算法就能找出学习数据的方法,并处理这些数据。这真是太神奇了,这也告诉我们通用人工智能是可行的,存在的!!!
8.3 模型展示1
神经元模型:逻辑回归
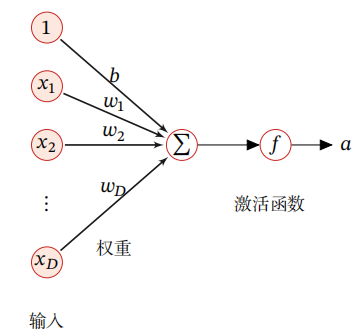
f = h θ ( x ) = 1 1 + e − θ T x f = {h_\theta }(x) = {1 \over {1 + {e^{ - {\theta ^T}x}}}} f=hθ(x)=1+e−θTx1

Θ \Theta Θ表示参数矩阵; Θ i j ( l ) \Theta _{ij}^{(l)} Θij(l)表示第 l l l个参数矩阵当前层的第 i i i个神经元与上一层的第 j j j个神经元的权重。
注意:本课程是按照输入层为第一层计算的。
8.4 模型展示2
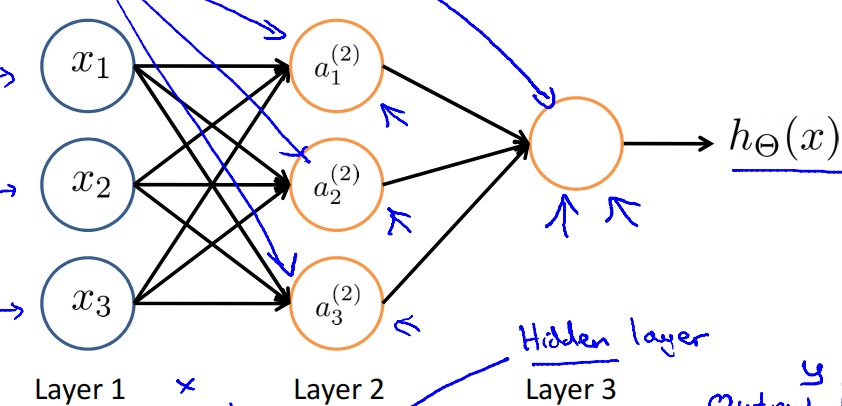
该神经网络的前向传播(forward propagation)
a 1 ( 2 ) = g ( Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 ) a_1^{(2)} = g(\Theta _{10}^{(1)}{x_0} + \Theta _{11}^{(1)}{x_1} + \Theta _{12}^{(1)}{x_2} + \Theta _{13}^{(1)}{x_3}) a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)
a 2 ( 2 ) = g ( Θ 20 ( 1 ) x 0 + Θ 21 ( 1 ) x 1 + Θ 22 ( 1 ) x 2 + Θ 23 ( 1 ) x 3 ) a_2^{(2)} = g(\Theta _{20}^{(1)}{x_0} + \Theta _{21}^{(1)}{x_1} + \Theta _{22}^{(1)}{x_2} + \Theta _{23}^{(1)}{x_3}) a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)
a 1 ( 2 ) = g ( Θ 30 ( 1 ) x 0 + Θ 31 ( 1 ) x 1 + Θ 32 ( 1 ) x 2 + Θ 33 ( 1 ) x 3 ) a_1^{(2)} = g(\Theta _{30}^{(1)}{x_0} + \Theta _{31}^{(1)}{x_1} + \Theta _{32}^{(1)}{x_2} + \Theta _{33}^{(1)}{x_3}) a1(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)
h θ ( x ) = g ( Θ 10 ( 2 ) a 0 ( 2 ) + Θ 11 ( 2 ) a 1 ( 2 ) + Θ 12 ( 2 ) a 2 ( 2 ) + Θ 13 ( 2 ) a 3 ( 2 ) ) {h_\theta }(x) = g(\Theta _{10}^{(2)}a_0^{(2)} + \Theta _{11}^{(2)}a_1^{(2)} + \Theta _{12}^{(2)}a_2^{(2)} + \Theta _{13}^{(2)}a_3^{(2)}) hθ(x)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))
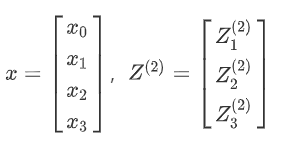
Z
(
2
)
=
Θ
(
1
)
x
=
Θ
(
1
)
a
(
1
)
{Z^{(2)}} = {\Theta ^{(1)}}x = {\Theta ^{(1)}}{a^{(1)}}
Z(2)=Θ(1)x=Θ(1)a(1),对于第一层
x
=
a
(
1
)
x = {a^{(1)}}
x=a(1)
a ( 2 ) = g ( Z ( 2 ) ) {a^{(2)}} = g({Z^{(2)}}) a(2)=g(Z(2)), Z ( 3 ) = Θ ( 2 ) a ( 2 ) {Z^{(3)}} = {\Theta ^{(2)}}{a^{(2)}} Z(3)=Θ(2)a(2), h θ ( x ) = a ( 3 ) = g ( Z ( 3 ) ) {h_\theta }(x) = {a^{(3)}} = g({Z^{(3)}}) hθ(x)=a(3)=g(Z(3))
8.5 示例与直观解释1
非线性分类器可以处理异或问题,而线性分类器不行。
8.6 示例与直观解释2
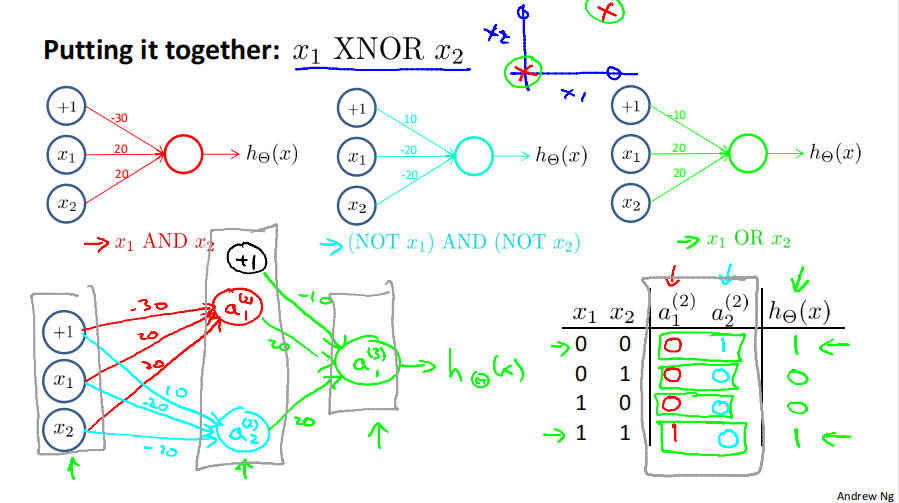
8.7 多分类
最后输出层输出n维向量,每一维表示是这一类的概率。





 本文概述了逻辑回归的决策边界、损失函数优化及正则化应用,然后探讨了神经网络如何处理非线性假设,包括多分类问题和正则化的使用。重点介绍了神经元模型和实际案例,展示了从线性到复杂非线性的模型转变。
本文概述了逻辑回归的决策边界、损失函数优化及正则化应用,然后探讨了神经网络如何处理非线性假设,包括多分类问题和正则化的使用。重点介绍了神经元模型和实际案例,展示了从线性到复杂非线性的模型转变。

















 5491
5491

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








