正则化

正则化（解决过拟合）

1. 过拟合问题

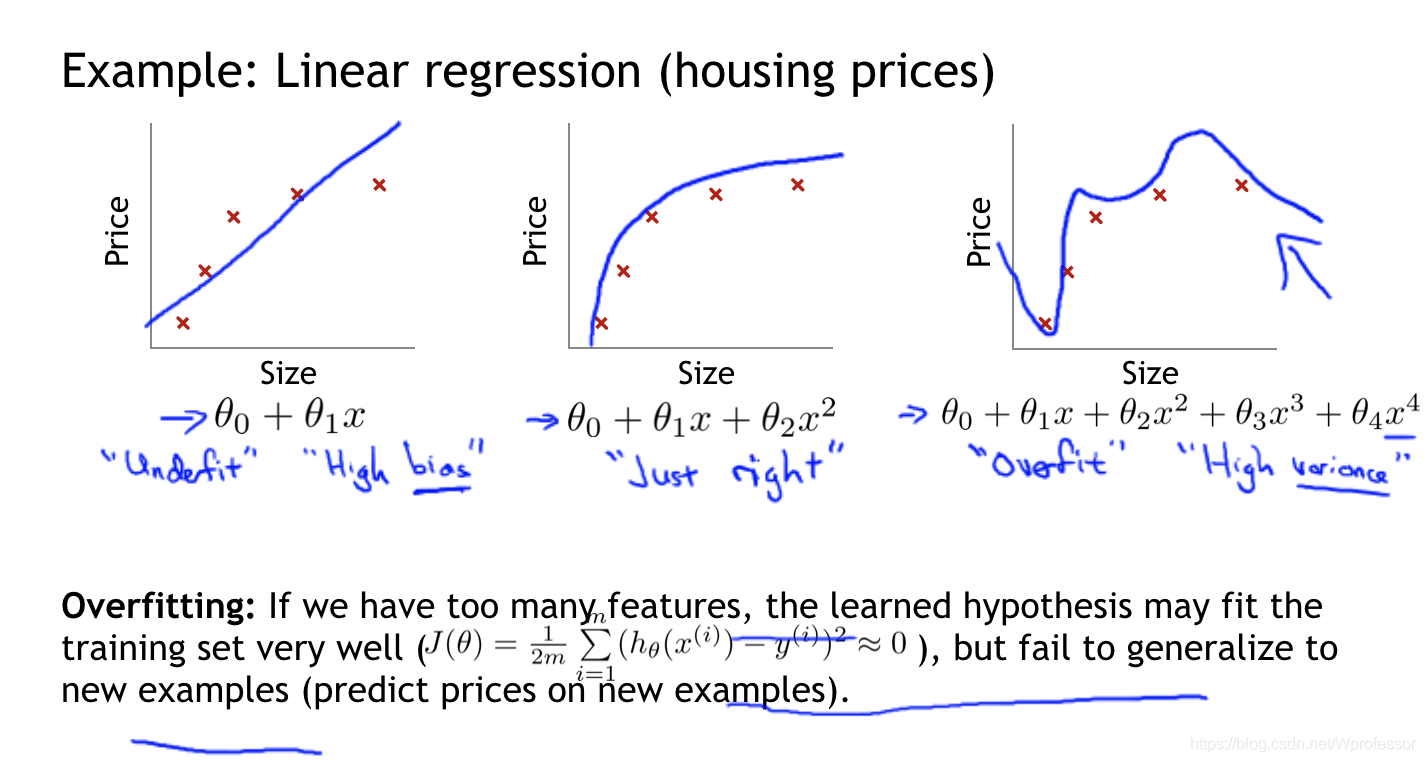
eg1：线性回归

很明显的图一为欠拟合，高偏差。

图三为过拟合，高方差，低偏差。一般过拟合对训练数据有很好的拟和能力，但对与新样本的泛化能力却很差。

eg2：逻辑回归

图一为欠拟合，高偏差。

图三为过拟合，高方差，低偏差。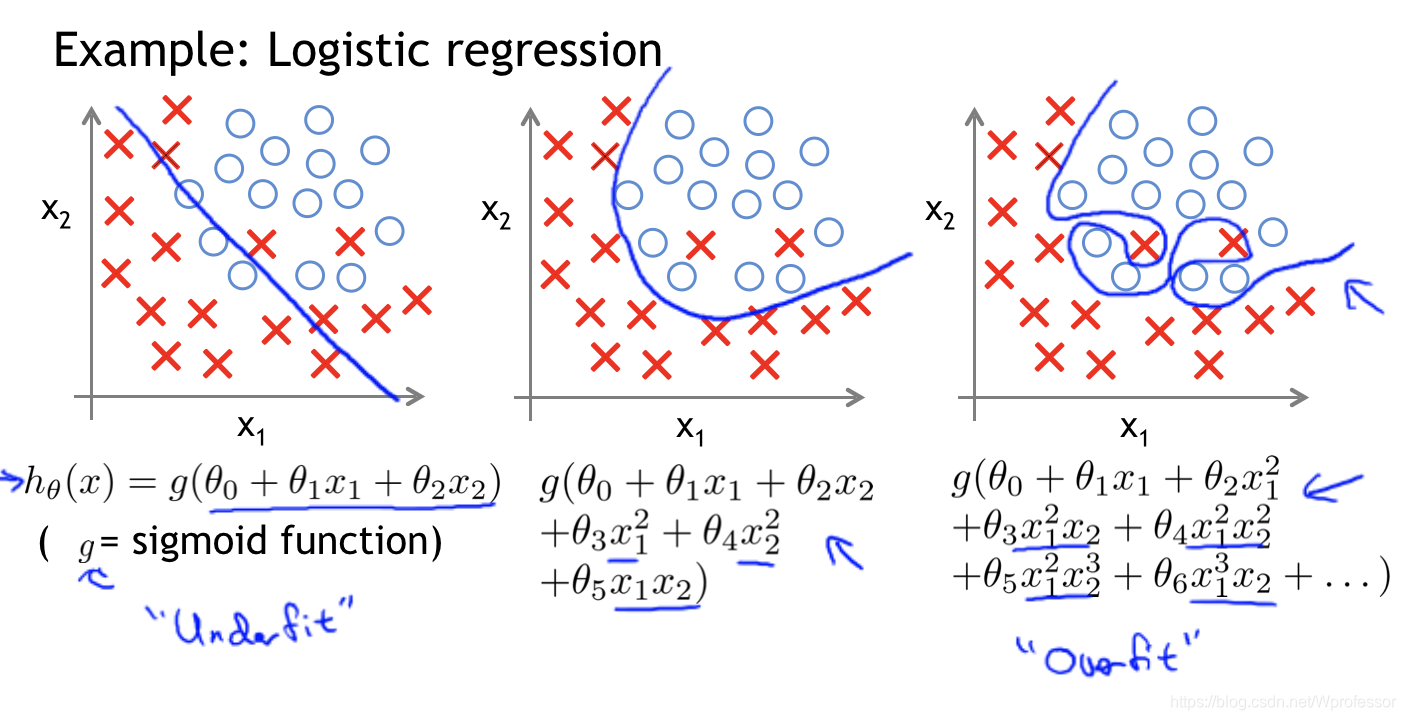

如果们的模型复杂度较高，而训练样本过少，通常会出现过拟合问题。

解决方法

1. 减少变量的数量，降低模型的复杂度

2. 正则化：保留所有，降低变量的权值。

2. 损失函数

如最上面图三的例子，我们可以在损失函数中加入惩罚项，也就是正则项，在最小化函数后面给每个变量的平方都乘以一个大的值，那么想让损失函数变小，这些变量就要接近0，这样就相当于变相弱化了这些对式子的影响。

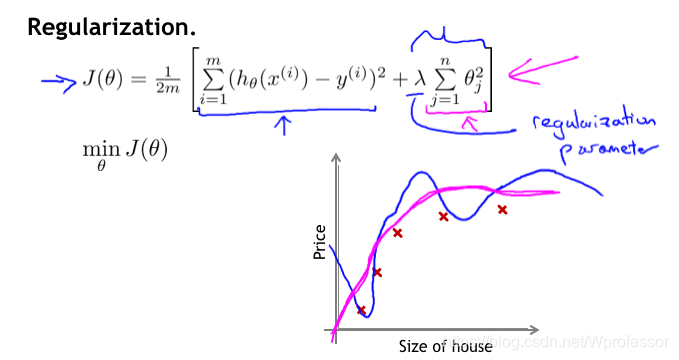
通过后面的累加项，就可以起到惩罚的作用

注意：在标准方程法中，如果训练数据集的数量小于特征的数量，那么就会出现奇异矩阵，导致X转置*X不可逆，此时加入正则化项也会解决这个问题。

参考文章：
https://blog.youkuaiyun.com/cheneykl/article/details/78685384
《吴恩达机器学习》