循环队列的C++实现

同栈一样，队列也是操作受限的线性表

两种存储结构：顺序存储结构和链式存储结构

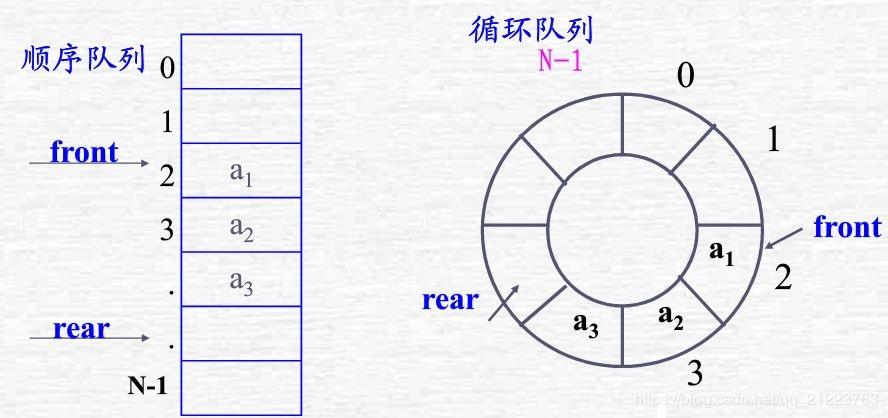
 循环队列

用一个数组存储队列，按照“先进先出”的原则，一般设计成如右图的循环队列，注意"假溢出"的问题：rear始终加1，不能再入队了，但实际上出队前面还有空位置；变成循环队列之后，究竟如何判断队列为满？：队列大小为m时，有m-1个元素就认为是队满。

#pragma once
#include<iostream>
using namespace std;

const int MAXSIZE = 10;
const int ERROR = 0;
const int OK = 1;
typedef int ElemType;

class Myqueue
{
public:
	Myqueue();
	int Queue_Length();
	bool Queue_Push(ElemType record);//入队
	bool Queue_Pop();                //出队
	ElemType GetHead();              //获得队头元素
	~Myqueue();
private:
	ElemType* base;
	int front;
	int rear;
};

Myqueue::Myqueue()
{
	this->base = new ElemType[MAXSIZE];
	this->front = 0;
	this->rear = 0;
}

int Myqueue::Queue_Length()//因为是循环队列
{
	return (rear - front + MAXSIZE) % MAXSIZE;//循环的原因不要返回rear-front
}

bool Myqueue::Queue_Push(ElemType record)
{
	if ((this->rear + 1) % MAXSIZE == this->front)//作为循坏队列的队满的条件
		return false;
	base[this->rear] = record;
	this->rear = (this->rear + 1) % MAXSIZE;//不再rear++，而是采用循环的rear = (rear + 1) % MAXSIZE
	return true;
}

bool Myqueue::Queue_Pop()
{
	if (this->front == this->rear)
		return false;
	this->front = (this->front + 1 ) % MAXSIZE;
}

ElemType Myqueue::GetHead()
{
	if (this->front == this->rear)
		return false;
	return base[this->front];
}

Myqueue::~Myqueue()
{
	if (base)
	{
		delete[] this->base;
		this->base = NULL;
	}
	this->front = 0;
	this->rear = 0;
}

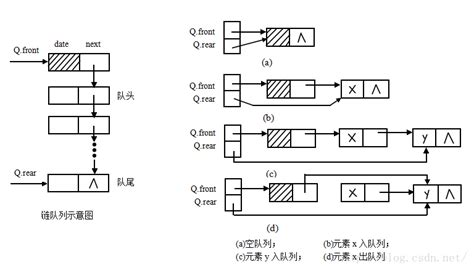
 队列的链式存储

只有链式存储结构的表示，没有入队、出队等基本操作

class Node
{
	ElemType data;
	Node* next;
};
class LinkQueue
{
	Node* front;//队头指针
	Node* rear;//队尾指针
};
//入队不需要判断队满，出队需要判断队列是否为空，注意在链队出队操作时，
// 入队时，采用尾插法
//队列中的最后一个元素被删除时，队尾指针也丢失了,需要对队尾指针进行重新赋值(指向头节点)