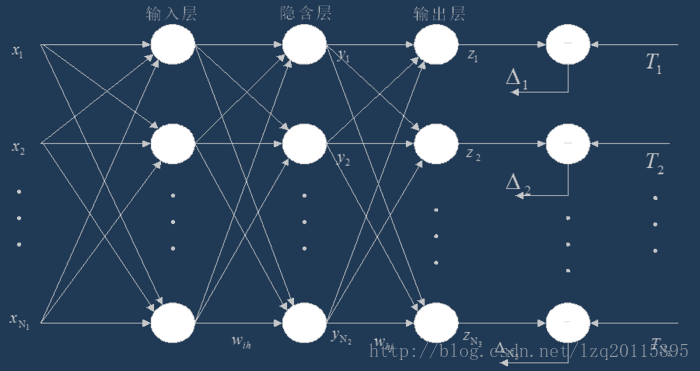
BP神经网络由两部分组成:
- 前馈神经网络:神经网络是前馈的,其权重都不回送到输入单元,或前一层输出单元(数据信息是单向传播的,不会回流),区别于循环神经网络RNN。
- BP算法(Back Propagation):误差反向传播算法,用于更新网络中的权重。
-
BP神经网络思想:
表面上:1. 数据信息的前向传播,从输入层到隐含层,最后到输出层。2. 误差的反向传播:输出结果与真实结果的误差值,从输出层传递到隐含层,最后到输入层。
本质上:针对每个输入样本,采用随机梯度下降算法,动态更新网络中的权重和偏倚,以使网络的输出不断地接近期望的输出。 -
-
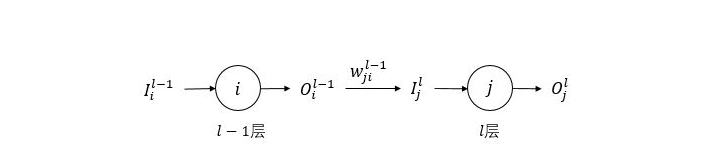
-
首先在BP神经网络模型中我们讨论前向传播,对于一个
 层的BP神经网络,其输入层为第
层的BP神经网络,其输入层为第 层,输出层为第
层,输出层为第 层,隐藏层为第
层,隐藏层为第 层到第
层到第 层。对于输出层的第
层。对于输出层的第 个神经元,其输出为
个神经元,其输出为 ,下标
,下标 表示第
表示第 个,上标
个,上标 表示层数,输入为
表示层数,输入为 。第
。第 层包含的神经元个数用
层包含的神经元个数用 表示。
表示。 -
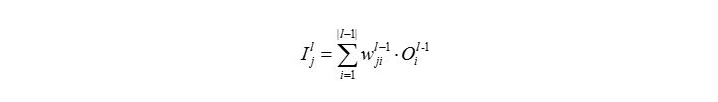
-
在下面的表述中为了描述的更加清楚我将不使用阈值
 (可以理解为内部偏置),即第
(可以理解为内部偏置),即第 层的第
层的第 个神经元的输入
个神经元的输入 与第
与第 每个神经元的输出关系如下所示,其中
每个神经元的输出关系如下所示,其中 表示第
表示第 层第
层第 个神经元与第
个神经元与第 层第个i 经元的链接权重。
层第个i 经元的链接权重。 -
(也就是说下一层某一神经元的输入来源于上一层每一个神经元的输出与权重加权和)
-
而输出
 ,
, 为激励函数。
为激励函数。 -
一般来说在神经网络中我们选择的激励函数
 是指
是指 函数,即
函数,即
-
可以更好的拟合非线性函数,且有
-
 ,即
,即 。
。 -
这里的反向误差减小采取更改权重值
-
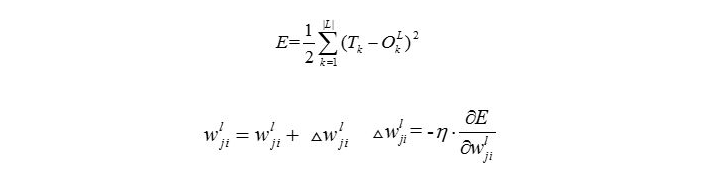
-
E为损失函数,偏导也就是梯度,乘以的系数为步数,类似于SGD
-
这里给出的也就是梯度下降的方向
-
引入新变量梯度
 ,对于第
,对于第 层第
层第 个神经元的梯度
个神经元的梯度,我们定义其值为
(***)
-
看输出层,即第 层,由于权重
层,由于权重 只对输出层的第
只对输出层的第 个单元产生影响,即只影响
个单元产生影响,即只影响 ,所以我们直接求导
,所以我们直接求导
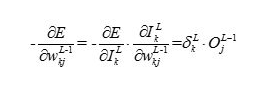 (M)
(M)
前面已知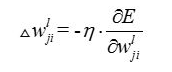 ,所以可以到
,所以可以到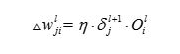 (G1)
(G1)

( 备注:看到这有人忘了O是什么了,O是某一层某一神经元的输出
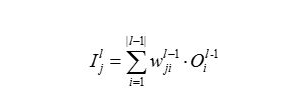 变形也就是
变形也就是![]() =
=![]()
前面提到的这个是说上一层神经元的输入乘以权重之和也就是下一层某一神经元的输入 )
下面尝试把梯度(***)给表示出来
根据 函数求导公式我们可以得到
函数求导公式我们可以得到 ,而误差
,而误差 如
如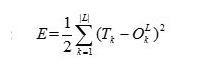 所示,所以我们可以得到
所示,所以我们可以得到 ,最后便得到了第
,最后便得到了第 层的每个神经单元的梯度项
层的每个神经单元的梯度项
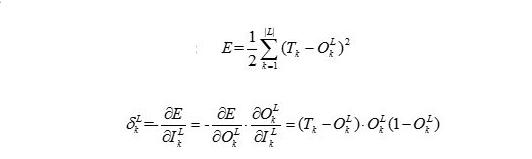 (G2)(两个G结合继续简化)
(G2)(两个G结合继续简化)
接下来是隐藏层
,这里对 进行推导,其他隐藏层以及输入层类似,显然
进行推导,其他隐藏层以及输入层类似,显然 虽然只影响第
虽然只影响第 层的第
层的第 个单元,但
个单元,但 层的第
层的第 个单元却链接了输出层的所有单元,所以
个单元却链接了输出层的所有单元,所以 对输出层的每一个单元都产生了影响。我们需要在求导的时它对输出层单元的每个误差的影响进行叠加,与输出层类似部分就不再累述。类似于上述M,得到下面关于L-2层的权重偏导
对输出层的每一个单元都产生了影响。我们需要在求导的时它对输出层单元的每个误差的影响进行叠加,与输出层类似部分就不再累述。类似于上述M,得到下面关于L-2层的权重偏导
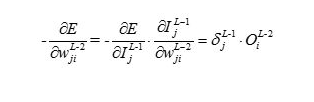
对于第 层的第
层的第 个神经单元的梯度项
个神经单元的梯度项来说,由于这个神经单元链接了输出层的每个单元,所以我们需要对输出层
 个单元求和,于是便得到了梯度项
个单元求和,于是便得到了梯度项的计算公式
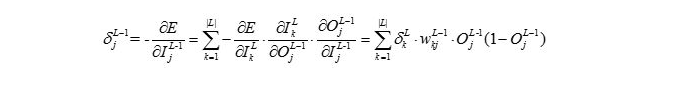
结合上述G2对比,发现这里到L层的输入跑了一遍,就是为了达到求和的目的,因为影响到了L层的全部
所以便得到了 层与
层与 层的链接权重
层的链接权重 更新公式
更新公式
![]() (与G1类似,区别在于
(与G1类似,区别在于![]() 的过程有区别)
的过程有区别)
输出层 对
对 (损失函数求导)求导,
(损失函数求导)求导, 对
对 (激活函数求导)求导,
(激活函数求导)求导, 再对
再对 (上一层的输出)求导(其中
(上一层的输出)求导(其中 ,
, ,
, 表示其计算公式)
表示其计算公式)
这样思考(E为L的损失函数,哪里找损失原因,看L层的输出,L层输出哪来的,L层的输入通过激活函数来的,那么输入怎么来的,上一层的输出通过w权重来的)
隐层就是判断一下求和的操作
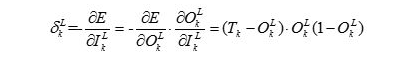
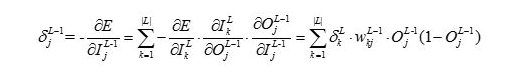
也就是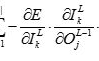 强行到下一层的输入跑了一遍,来表示影响了下一层的全部输出(输出来源于输入)
强行到下一层的输入跑了一遍,来表示影响了下一层的全部输出(输出来源于输入)
再次表明(梯度就是损失值与输入的偏导),这一层的输入表示不了,我们跑一下输出来表示
隐层再跑一下下一层输入来表示影响全部
算法实验待更
到了再说





 本文深入解析BP神经网络的工作原理,包括前馈神经网络的数据信息前向传播和BP算法的误差反向传播。通过数学推导,阐述了如何利用随机梯度下降算法动态更新网络权重,以使网络输出接近期望值。
本文深入解析BP神经网络的工作原理,包括前馈神经网络的数据信息前向传播和BP算法的误差反向传播。通过数学推导,阐述了如何利用随机梯度下降算法动态更新网络权重,以使网络输出接近期望值。
















 2607
2607

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








