BM58-字符串的排列

题目

输入一个长度为 n 字符串，打印出该字符串中字符的所有排列，你可以以任意顺序返回这个字符串数组。

例如输入字符串ABC,则输出由字符A,B,C所能排列出来的所有字符串ABC,ACB,BAC,BCA,CBA和CAB。

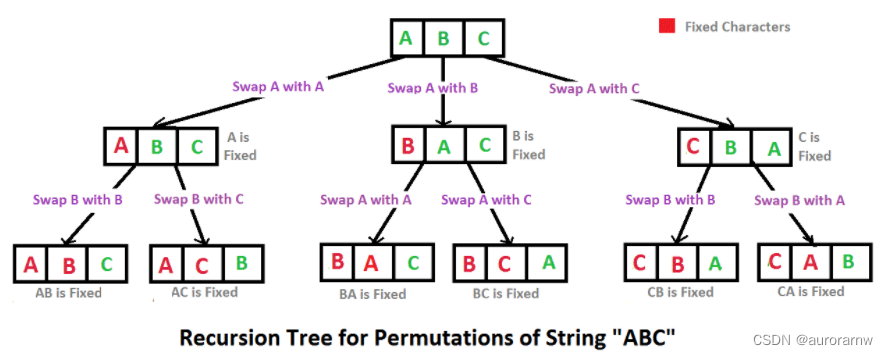
数据范围：n < 10。
要求：空间复杂度 O(n!)，时间复杂度 O(n!)。

输入描述：输入一个字符串,长度不超过10,字符只包括大小写字母。

示例1

输入："ab"

返回值：["ab","ba"]

说明：返回["ba","ab"]也是正确的

示例2

输入："aab"

返回值：["aab","aba","baa"]

示例3

输入："abc"

返回值：["abc","acb","bac","bca","cab","cba"]

示例4

输入：""

返回值：[""]

---

思路：递归+回溯

可参考：

字符串的排列http://t.csdn.cn/aOxb2

• 递归是一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。因此递归过程，最重要的就是查看能不能讲原本的问题分解为更小的子问题，这是使用递归的关键。
• 如果是线型递归，子问题直接回到父问题不需要回溯，但是如果是树型递归，父问题有很多分支，我需要从子问题回到父问题，进入另一个子问题。因此回溯是指在递归过程中，从某一分支的子问题回到父问题进入父问题的另一子问题分支，因为有时候进入第一个子问题的时候修改过一些变量，因此回溯的时候会要求改回父问题时的样子才能进入第二子问题分支。

都是求元素的全排列，字符串与数组没有区别，一个是数字全排列，一个是字符全排列，因此大致思路与有重复项的数字的全排列类似，只是这道题输出顺序没有要求。但是为了便于去掉重复情况，我们还是应该参照数组全排列，优先按照字典序排序，因为排序后重复的字符就会相邻，后续递归找起来也很方便。

使用临时变量去组装一个排列的情况：每当我们选取一个字符以后，就确定了其位置，相当于对字符串中剩下的元素进行全排列添加在该元素后面，给剩余部分进行全排列就是一个子问题，因此可以使用递归。

• 终止条件： 临时字符串中选取了n个元素，已经形成了一种排列情况了，可以将其加入输出数组中。
• 返回值： 每一层给上一层返回的就是本层级在临时字符串中添加的元素，递归到末尾的时候就能添加全部元素。
• 本级任务： 每一级都需要选择一个元素加入到临时字符串末尾（遍历原字符串选择）。

递归过程也需要回溯，比如说对于字符串“abbc”，如果事先在临时字符串中加入了a，后续子问题只能是"bbc"的全排列接在a后面，对于b开头的分支达不到，因此也需要回溯：将临时字符串刚刚加入的字符去掉，同时vis修改为没有加入，这样才能正常进入别的分支。

具体做法：

• step 1：先对字符串按照字典序排序，获取第一个排列情况。
• step 2：准备一个空串暂存递归过程中组装的排列情况。使用额外的vis数组用于记录哪些位置的字符被加入了。
• step 3：每次递归从头遍历字符串，获取字符加入：首先根据vis数组，已经加入的元素不能再次加入了；同时，如果当前的元素str[i]与同一层的前一个元素str[i-1]相同且str[i-1]已经用过，也不需要将其纳入。
• step 4：进入下一层递归前将vis数组当前位置标记为使用过。
• step 5：回溯的时候需要修改vis数组当前位置标记，同时去掉刚刚加入字符串的元素。
• step 6：临时字符串长度到达原串长度就是一种排列情况。

---

代码

import java.util.*;

public class Solution {
    public ArrayList<String> Permutation(String str) {
        ArrayList<String> res = new ArrayList<String>();
        if (str == null || str.length() == 0) {
            return res;
        }
        //转字符数组
        char[] charStr = str.toCharArray();
        // 按字典序排序
        Arrays.sort(charStr);
        boolean[] vis = new boolean[str.length()];
        //标记每个位置的字符是否被使用过
        Arrays.fill(vis, false);
        StringBuffer temp = new StringBuffer();
        //递归获取
        recursion(res, charStr, temp, vis);
        return res;
    }

    public void recursion(ArrayList<String> res, char[] str, StringBuffer temp, boolean[] vis) {
        //临时字符串满了加入输出
        if (temp.length() == str.length) {
            res.add(new String(temp));
            return;
        }
        //遍历所有元素选取一个加入
        for (int i = 0; i < str.length; i++) {
            //如果该元素已经被加入了则不需要再加入了
            if (vis[i]) {
                 continue;
            }
            if (i > 0 && str[i - 1] == str[i] && !vis[i - 1]) {
                //当前的元素str[i]与同一层的前一个元素str[i-1]相同且str[i-1]已经用过了
                continue;
            }
            //标记为使用过
            vis[i] = true;
            //加入临时字符串
            temp.append(str[i]);
            recursion(res, str, temp, vis);
            //回溯
            vis[i] = false;
            temp.deleteCharAt(temp.length() - 1);
        }
    }
}