48-优先级队列

Java优先级队列(PriorityQueue)原理与应用

原创已于 2023-04-25 23:28:17 修改 · 426 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构

于 2023-04-01 08:02:47 首次发布

Java数据结构专栏收录该内容

79 篇文章

订阅专栏

Java元素的比较http://t.csdn.cn/rJ8fM

1.概念

在很多应用中，我们通常需要按照优先级情况对待处理对象进行处理，比如首先处理优先级最高的对象，然后处理次高的对象。

在这种情况下，数据结构应该提供2个最基本的操作：一个是返回最高优先级对象，一个是添加新的对象。这种数据结构就是优先级队列（Priority Queue）。

2.内部原理

优先级队列的实现方式很多，最常见的是用堆来构建。其底层是基于堆来实现的，仍满足队列的3大操作。（还是队列，不过套了堆的包装）。

3.操作

入队列：调用堆的add方法。
出队列：按照优先级出队列，优先级最高的先出（堆顶元素），调用堆的extractMax方法。
查看队首元素：即堆顶元素。

4.应用

医生排患者手术名单，优先级就是病情严重程度，相同严重程度再看时间先后。
操作系统的作业（进程/任务）调度。

5.代码实现

import heap.MaxHeap;

public class PriorityQueue implements Queue {
    private MaxHeap heap = new MaxHeap();

    @Override
    public void offer(int value) {
        heap.add(value);
    }

    @Override
    public int poll() {
        return heap.extractMax();
    }

    @Override
    public int peek() {
        return heap.peekHeap();
    }
}

import java.util.Arrays;

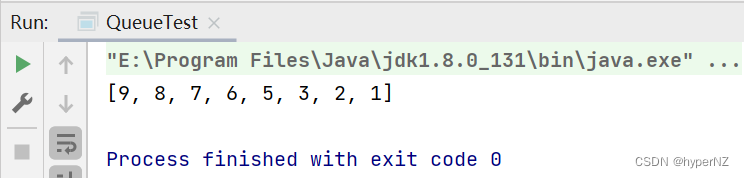
public class QueueTest {
    public static void main(String[] args) {
        int[] arr = {3, 5, 2, 1, 7, 6, 9, 8};
        Queue queue = new PriorityQueue(); //降序排列
        for(int i : arr) {
            queue.offer(i);
        }
        for (int i = 0; i < arr.length; i++) {
            arr[i] = queue.poll();
        }
        System.out.println(Arrays.toString(arr));
    }
}

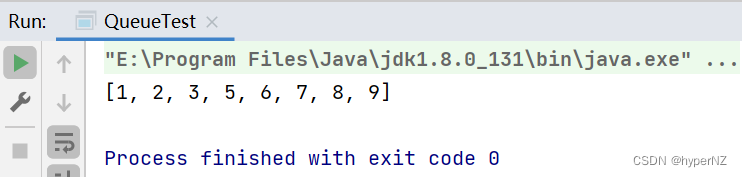
import java.util.Arrays;
import java.util.PriorityQueue;

public class QueueTest {
    public static void main(String[] args) {
        int[] arr = {3, 5, 2, 1, 7, 6, 9, 8};
        PriorityQueue<Integer> queue = new PriorityQueue<>(); //升序排序，JDK中的PriorityQueue是基于最小堆实现的
//        Queue queue = new PriorityQueue(); //降序排列
        for(int i : arr) {
            queue.offer(i);
        }
        for (int i = 0; i < arr.length; i++) {
            arr[i] = queue.poll();
        }
        System.out.println(Arrays.toString(arr));
    }
}

PS：源码分析：
private void siftUp(int k, E x) {
    if (comparator != null)
        siftUpUsingComparator(k, x);
    else
        siftUpComparable(k, x);
}
当使用JDK的优先级队列时，若传入的是自定义类型，如Student，

要么向优先级队列中传入该类的比较器。
public PriorityQueue(Comparator<? super E> comparator) {
    this(DEFAULT_INITIAL_CAPACITY, comparator);
}
要么自定义的类型实现了Comparable接口。

JDK内置的类，如String，包装类等都默认是Comparable的子类。
private void siftUpComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>) x;
    while (k > 0) {
        int parent = (k - 1) >>> 1;
        Object e = queue[parent];
        if (key.compareTo((E) e) >= 0)
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = key;
}
e是父节点的值，key是子节点的值。if分支说明当前节点 >= 父节点，停止。

父节点 < 子节点，堆顶存放的就是最小值，最小堆。

要想通过CompareTo方法改造为最大堆，则this.val < o.val =>return 1;

根据JDK代码，就把小的值留在子节点，大的值跑上面了，变为最大堆。