路径之谜

题目描述

小明冒充 XX 星球的骑士，进入了一个奇怪的城堡。

城堡里边什么都没有，只有方形石头铺成的地面。

假设城堡地面是 n×nn×n 个方格。如下图所示。

按习俗，骑士要从西北角走到东南角。可以横向或纵向移动，但不能斜着走，也不能跳跃。每走到一个新方格，就要向正北方和正西方各射一箭。（城堡的西墙和北墙内各有 nn 个靶子）同一个方格只允许经过一次。但不必走完所有的方格。如果只给出靶子上箭的数目，你能推断出骑士的行走路线吗？有时是可以的，比如上图中的例子。

本题的要求就是已知箭靶数字，求骑士的行走路径（测试数据保证路径唯一）

输入描述

第一行一个整数 NN (0≤N≤200≤N≤20)，表示地面有 N×NN×N 个方格。

第二行 NN 个整数，空格分开，表示北边的箭靶上的数字（自西向东）

第三行 NN 个整数，空格分开，表示西边的箭靶上的数字（自北向南）

输出描述

输出一行若干个整数，表示骑士路径。

为了方便表示，我们约定每个小格子用一个数字代表，从西北角开始编号: 0,1,2,3 ⋯⋯

比如，上图中的方块编号为：

0 1 2 3

4 5 6 7

8 9 10 11

12 13 14 15

输入输出样例

示例

输入

4
2 4 3 4
4 3 3 3

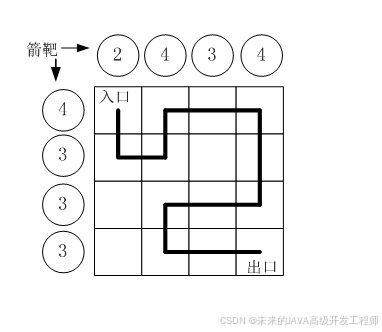
输出

0 4 5 1 2 3 7 11 10 9 13 14 15

import java.util.*;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    static int n;
	static int[] ai, bi;//北墙和西墙箭靶
	static boolean[][] loop;//标记是否走过
	static int[] xi = {-1,0,1,0};//偏移量
	static int[] yi = {0,1,0,-1};
	static List<Integer> list = new ArrayList<>();//存储走的路径
	public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		n = scanner.nextInt();
		ai = new int[n];
		bi = new int[n];
		loop = new boolean[n][n];
		for (int i = 0; i < n; i++) {
			ai[i] = scanner.nextInt();
		}
		for (int i = 0; i < n; i++) {
			bi[i] = scanner.nextInt();
		}
		loop[0][0] = true;//起点已经走过
		ai[0]--;bi[0]--;
		list.add(0);
		dfs(0, 0);
	}
	private static void dfs(int x, int y) {
		if(x == n-1 && y == n-1) {
			//如果走到终点
			for (int i = 0; i < n; i++) {
				if (ai[i]!=0 || bi[i] != 0) {
					return;//不满足
				}
			}
			for (int lj : list) {
				System.out.print(lj + " ");
			}
			return;
		}
		//核心代码
		for (int i = 0; i < 4; i++) {
			int xx = x + xi[i];
			int yy = y + yi[i];
			if (check(xx, yy)) {
				ai[yy]--;bi[xx]--;
				loop[xx][yy]=true;
				list.add(xx * n + yy);
				dfs(xx, yy);
				//回溯
				list.remove(list.size() - 1);
				loop[xx][yy]=false;
				ai[yy]++;bi[xx]++;
			}
		}
		
	}
	private static boolean check(int xx, int yy) {
		if(xx<0 || yy<0 || xx>=n || yy>=n || loop[xx][yy]) {
			return false;
		}
		if(bi[xx]-1 < 0 || ai[yy]-1 < 0) {
			return false;
		}
		return true;
	}
}