LeetCode刷题笔记（Sum of Left Leaves）

刚刚又刷了一道题目，下面就和大家分享一下经验吧！

题目如下：

Find the sum of all left leaves in a given binary tree.

Example:

    3
   / \
  9  20
    /  \
   15   7

There are two left leaves in the binary tree, with values 9 and 15 respectively. Return 24.

题意分析：

给定一个二叉树，请计算该树左叶子节点值之和。

方法一（递归法）

因为只需要计算左叶子节点值之和，所以在进行递归调用时需要知道当前结点是否是左节点，如果是左节点且该左节点并没有子节点，则说明其是左叶子节点，于是可以将其值累加到res中。另外采用一个bool型的变量去区别是左节点还是右节点，如果为true则说明当前结点为左（叶子）节点，若为false则说明是右（叶子）节点。遍历二叉树完毕后，返回res值即可。

解题代码如下：

class Solution{
public:
    int sumOfLeftLeaves(TreeNode* root){
        if(!root || (!root->left && !root->right)) return 0;
        int res = 0;
        seek_left_value(root->left, true, res);
        seek_left_value(root->right, false, res);
        return res;
    }
    void  seek_left_value(TreeNode* root, bool left, int& res ){
        if(!root) return;
        if(!root->left && !root->right && left == true) res = res + root->val;
        seek_left_value(root->left, true, res);
        seek_left_value(root->right, false, res);
     }
};

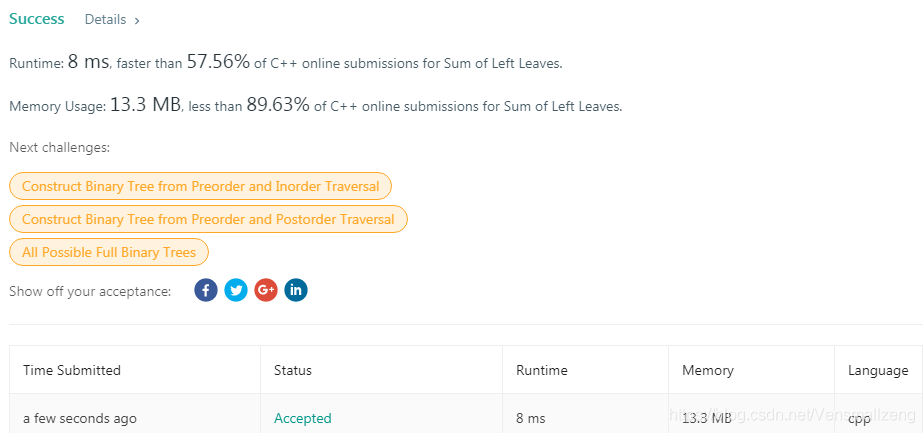
提交后的结果如下：

方法二（递归法）

方法一中定义了一个函数，其实可以直接在原函数中判断当前节点的左节点是否是左叶子节点，如果是则返回“左叶子节点的值”+“对当前结点的右节点递归调用的值”；如果不是则分别对左右节点进行递归调用，最终返回二者之和即可。

解题代码如下：

class Solution{
public:
    int sumOfLeftLeaves(TreeNode* root){
        if(!root) return 0;
        if(root->left && !root->left->left && !root->left->right) return root->left->val + sumOfLeftLeaves(root->right);
        return sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);
    }
};

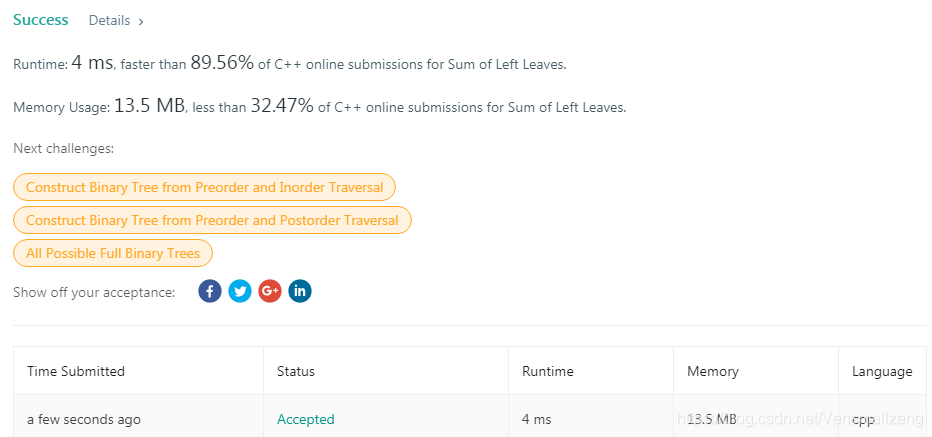
提交后的结果如下：

 

 

 

日积月累，与君共进，增增小结，未完待续。